程序员的算法课（8）-贪心算法：理解霍夫曼编码

一、一种很贪婪的算法定义

贪心是人类自带的能力，贪心算法是在贪心决策上进行统筹规划的统称。

【百度百科】贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。

二、贪心跟动态规划

贪心选择

贪心选择是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。这是贪心算法可行的第一个基本要素，也是贪心算法与动态规划算法的主要区别。贪心选择是采用从顶向下、以迭代的方法做出相继选择，每做一次贪心选择就将所求问题简化为一个规模更小的子问题。对于一个具体问题，要确定它是否具有贪心选择的性质，我们必须证明每一步所作的贪心选择最终能得到问题的最优解。通常可以首先证明问题的一个整体最优解，是从贪心选择开始的，而且作了贪心选择后，原问题简化为一个规模更小的类似子问题。然后，用数学归纳法证明，通过每一步贪心选择，最终可得到问题的一个整体最优解。

最优子结构

当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。运用贪心策略在每一次转化时都取得了最优解。问题的最优子结构性质是该问题可用贪心算法或动态规划算法求解的关键特征。贪心算法的每一次操作都对结果产生直接影响，而动态规划则不是。贪心算法对每个子问题的解决方案都做出选择，不能回退；动态规划则会根据以前的选择结果对当前进行选择，有回退功能。动态规划主要运用于二维或三维问题，而贪心一般是一维问题 。

总结

1. 贪心算法是自顶向下的，而动态规划则是自底向上的。
2. 动态规划是自底向上求出各子问题的有化解，最后汇集有化解从而得出问题的全局最优解（可以想象成各个小河流入大海） 。
3. 贪心算法是自顶下向下，以迭代的方式一步一步做出贪心选择，从而把问题简化成规模更小的问题 。
4. 狭义的贪心算法指的是解最优化问题的一种特殊方法，解决过程中总是做出当下最好的选择，因为具有最优子结构的特点，局部最优解可以得到全局最优解；这种贪心算法是动态规划的一种特例。能用贪心解决的问题，也可以用动态规划解决。

三、贪婪算法的思想

贪心算法的基本思路是从问题的某一个初始解出发一步一步地进行，以尽可能快的地求得更好的解。根据某个优化测度，每一步都要确保能获得局部最优解。每一步只考虑一个数据，他的选取应该满足局部优化的条件。若下一个数据和部分最优解连在一起不再是可行解时，就不把该数据添加到部分解中，直到把所有数据枚举完，或者不能再添加时，算法停止。

该算法存在问题： 

1. 不能保证求得的最后解是最佳的； 
2. 不能用来求最大或最小解问题； 
3. 只能求满足某些约束条件的可行解的范围。 

实现该算法的过程： 

1. 从问题的某一初始解出发；
2. while 能朝给定总目标前进一步；
3. do 求出可行解的一个解元素；
4. 由所有解元素组合成问题的一个可行解。

四、贪心算法能解决哪些问题呢？

贪婪算法可解决的问题通常大部分都有如下的特性：

• 随着算法的进行，将积累起其它两个集合：一个包含已经被考虑过并被选出的候选对象，另一个包含已经被考虑过但被丢弃的候选对象。
• 有一个函数来检查一个候选对象的集合是否提供了问题的解答。该函数不考虑此时的解决方法是否最优。
• 还有一个函数检查是否一个候选对象的集合是可行的，也即是否可能往该集合上添加更多的候选对象以获得一个解。和上一个函数一样，此时不考虑解决方法的最优性。
• 选择函数可以指出哪一个剩余的候选对象最有希望构成问题的解。
• 最后，目标函数给出解的值。
• 为了解决问题，需要寻找一个构成解的候选对象集合，它可以优化目标函数，贪婪算法一步一步的进行。起初，算法选出的候选对象的集合为空。接下来的每一步中，根据选择函数，算法从剩余候选对象中选出最有希望构成解的对象。如果集合中加上该对象后不可行，那么该对象就被丢弃并不再考虑；否则就加到集合里。每一次都扩充集合，并检查该集合是否构成解。如果贪婪算法正确工作，那么找到的第一个解通常是最优的。

具体而言，0-1背包、单源最短路径、马踏棋盘、均分纸牌等问题都可以使用贪心算法来解决。

五、使用贪心算法如何解决霍夫曼编码

1.回顾一下霍夫曼编码

霍夫曼编码是广泛地用于数据文件压缩的十分有效的编码方法。其压缩率通常在20%～90%之间。哈夫曼编码算法用字符在文件中出现的频率表来建立一个用0，1串表示各字符的最优表示方式。

霍夫曼编码中，每个字符用唯一的一个0,1串表示，并且采用变长编码来表示每个字符，使用频率高的字符用较短的编码；使用频率低的字符用较长的编码，以达到整体文本编码缩小的目的。

对于霍夫曼解码，我们引入前缀码的概念：对每一个字符规定一个0,1串作为其代码，并要求任一字符的代码都不是其他字符代码的前缀。编码的前缀性质可以使译码方法非常简单；例如001011101可以唯一的分解为0,0,101,1101，因而其译码为aabe。

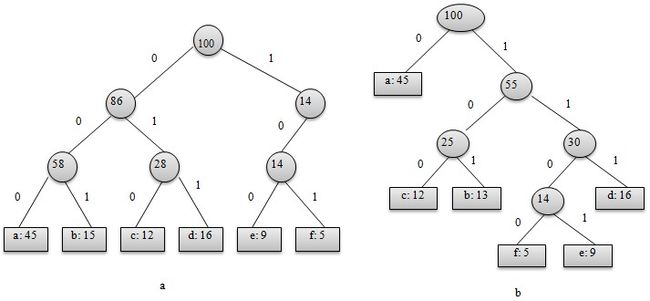
译码过程需要方便的取出编码的前缀，因此需要表示前缀码的合适的数据结构。为此，可以用二叉树作为前缀码的数据结构：树叶表示给定字符；从树根到树叶的路径当作该字符的前缀码；代码中每一位的0或1分别作为指示某节点到左儿子或右儿子的“路标”。

从上图可以看出，表示最优前缀码的二叉树总是一棵完全二叉树，即树中任意节点都有2个儿子。图a表示定长编码方案不是最优的，其编码的二叉树不是一棵完全二叉树。在一般情况下，若C是编码字符集，表示其最优前缀码的二叉树中恰有|C|个叶子。每个叶子对应于字符集中的一个字符，该二叉树有|C|-1个内部节点。

2.构造哈弗曼编码

哈夫曼提出构造最优前缀码的贪心算法，由此产生的编码方案称为哈夫曼编码。其构造步骤如下：

1. 哈夫曼算法以自底向上的方式构造表示最优前缀码的二叉树T。
2. 算法以|C|个叶结点开始，执行|C|－1次的“合并”运算后产生最终所要求的树T。
3. 假设编码字符集中每一字符c的频率是f(c)。以f为键值的优先队列Q用在贪心选择时有效地确定算法当前要合并的2棵具有最小频率的树。一旦2棵具有最小频率的树合并后，产生一棵新的树，其频率为合并的2棵树的频率之和，并将新树插入优先队列Q。经过n－1次的合并后，优先队列中只剩下一棵树，即所要求的树T。
4. 应该将概率低的元素放置到树的底部，将概率高的元素放置到树的顶部。

构造过程如图所示：

具体代码实现如下：

import java.util.ArrayList;
 
/**
 * 贪心算法解哈夫曼编码问题
 * 
 * @author wly
 * 
 */
public class HuffmanCode {
 
	public static void main(String[] args) {
 
		ArrayList list = new ArrayList();
 
		list.add(new HuffmanNode(null, null, "A", 0.3f));
		list.add(new HuffmanNode(null, null, "B", 0.1f));
		list.add(new HuffmanNode(null, null, "C", 0.35f));
		list.add(new HuffmanNode(null, null, "D", 0.05f));
		list.add(new HuffmanNode(null, null, "E", 0.2f));
 
		print(getHuffmanCodeNode(list));
	}
 
	/**
	 * 得到表示当前输入节点的树结构
	 * @param list
	 * @return
	 */
	public static HuffmanNode getHuffmanCodeNode(ArrayList list) {
 
		while (list.size() >= 2) {
			//1.排序元素
			srotNodeListByKey(list);
 
			//2.合并key值最小的两个节点(因为已经排序过了，此处就是列表的前两项)
			HuffmanNode newNode = combine2SmallestNode(list.get(0), list.get(1));
			list.remove(0);
			list.remove(0); //注意ArrayList中remove元素时的索引移动s
			list.add(0, newNode);
		}
		
		return list.get(0);
	}
	
	/**
	 * 打印某个节点的树结构，即以该节点为根节点的子树结构s
	 * @param node
	 */
	public static void print(HuffmanNode node) {
		System.out.print("| " + node.getData() + "," + node.getPercent() + " |");
		if(node.getLeftN() != null) {
			print(node.getLeftN());
		} 
		
		if(node.getRightN() != null) {
			print(node.getRightN());
		} 
	}	
	
	/**
	 * 使用冒泡排序，按key值单调递增排序
	 * 
	 * @param list
	 */
	public static void srotNodeListByKey(ArrayList list) {
		for (int i = 0; i < list.size(); i++) {
			for (int j = i+1; j < list.size(); j++) {
				if (list.get(i).getPercent() > list.get(j).getPercent()) {
					// 交换位置
					list.add(i, list.get(j));
					list.remove(j+1);
					
					list.add(j, list.get(i + 1));
					list.remove(i + 1);
				}
			}
		}
	}
 
 
	/**
	 * 将两个子节点合成为一个父节点
	 * 
	 * @param leftNode
	 * @param rightNode
	 * @return
	 */
	private static HuffmanNode combine2SmallestNode(HuffmanNode leftNode,
			HuffmanNode rightNode) {
		HuffmanNode parentNode = new HuffmanNode(leftNode, rightNode,
				leftNode.getData() + rightNode.getData(), leftNode.getPercent()
						+ rightNode.getPercent());
		return parentNode;
	}
}
 
/**
 * 用于表示哈夫曼编码的二叉树的节类
 * 
 * @author wly
 * 
 */
class HuffmanNode {
 
	private HuffmanNode leftN; //左子节点
	private HuffmanNode rightN; //右子节点
	private String data; // 包含的数据，本程序中指的是字符
	private float percent; // 检索key值
 
	public HuffmanNode(HuffmanNode leftN, HuffmanNode rightN, String data,
			float key) {
		super();
		this.leftN = leftN;
		this.rightN = rightN;
		this.data = data;
		this.percent = key;
	}
 
	public float getPercent() {
		return percent;
	}
 
	public void setPercent(float percent) {
		this.percent = percent;
	}
 
	public HuffmanNode getLeftN() {
		return leftN;
	}
 
	public void setLeftN(HuffmanNode leftN) {
		this.leftN = leftN;
	}
 
	public HuffmanNode getRightN() {
		return rightN;
	}
 
	public void setRightN(HuffmanNode rightN) {
		this.rightN = rightN;
	}
 
	public String getData() {
		return data;
	}
 
	public void setData(String data) {
		this.data = data;
	}
 
}

运行结果：

| DBEAC,1.0 || DBE,0.35000002 || DB,0.15 || D,0.05 || B,0.1 || E,0.2 || AC,0.65 || A,0.3 || C,0.35 |

从运行结果可以得到二叉树如下:

结论：

•  即各个字符的编码分别是:D:000、D:001、E:01、A:10、C:11
• 若不进行编码按相同字长编码，则至少需要3位，那么需要存储ABCDE的尺寸为:3*1=3
• 编码后，存储ABCDE的尺寸为:3*0.05+3*0.1+2*0.2+2*0.3+2*0.2=1.85
• 可见使用哈夫曼编码能够在一定程度上实现数据的无损压缩。

六、总结

1. 贪婪算法就是算法的每一步都是上一步条件下的最好选择。 贪婪算法得到的是一个近似最优解。 
2. 求最小生成树的Prim算法和Kruskal算法都是漂亮的贪心算法。
3. 贪心法的应用算法有Dijkstra的单源最短路径和Chvatal的贪心集合覆盖启发式。
4. 贪心算法可以与随机化算法一起使用，具体的例子就不再多举了。其实很多的智能算法（也叫启发式算法），本质上就是贪心算法和随机化算法结合——这样的算法结果虽然也是局部最优解，但是比单纯的贪心算法更靠近了最优解。例如遗传算法，模拟退火算法。
5. 贪婪算法可以寻找局部最优解，并尝试与这种方式获得全局最优解。
6. 得到的可能是近似最优解，但也可能便是最优解(区间调度问题，最短路径问题(广度优先、狄克斯特拉))。
7. 对于完全NP问题，目前并没有快速得到最优解的解决方案。
8. 面临NP完全问题，最佳的做法就是使用近似算法。
9. 贪婪算法(近似算法)在大部分情况下易于实现，并且效率不错。

---

我的微信公众号：架构真经（id：gentoo666），分享Java干货，高并发编程，热门技术教程，微服务及分布式技术，架构设计，区块链技术，人工智能，大数据，Java面试题，以及前沿热门资讯等。每日更新哦！

参考资料：

1. https://blog.csdn.net/jeffleo/article/details/53526721
2. https://blog.csdn.net/ftl111/article/details/79707452
3. https://www.jianshu.com/p/b613ae9d77ff
4. https://www.cnblogs.com/hust-chen/p/8646009.html
5. https://blog.csdn.net/likunkun__/article/details/80747566
6. https://blog.csdn.net/likunkun__/article/details/80258515
7. https://blog.csdn.net/liufeng_king/article/details/8720896
8. https://blog.csdn.net/u011638883/article/details/16857309