Diffusion MRI的纤维重建算法解析--DTI，ball-and-sticks model，CSD，DSI，QBI，GQI

一. 什么是纤维重建

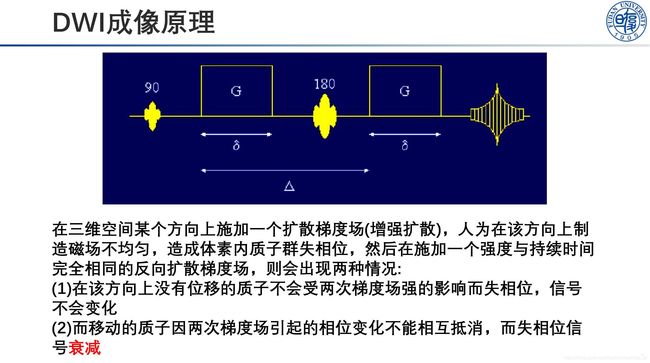
对结构MRI影像分析比较了解的话一定听过DTI，即DIffusion Tensor Image，初学时我以为DTI跟fMRI, T1类似，也是磁共振影像的一种，可以用来表征大脑内的神经纤维。但是这种认知是错误的，实际上应该是DWI（Diffusion Weighted Imaging），即扩散加权影像，它通过对水分子在多方向上的扩散程度进行成像，从而表征神经纤维的走向。

而DTI是一种纤维重建模型，使用数学模型的方法基于DWI影像计算神经纤维走向并进行纤维追踪，类似于解N阶多元方程，每一阶表示一个方向，阶数越多模拟出的纤维走向就越准确。

而纤维重建算法就不止DTI这一种了（如题所列），它们的区别是什么？原理是什么？

为了更好地理解每种重建方法的优缺点，可以将它们分为基于模型的方法（Model-based methods）或无模型方法（Model-free methods）。该分类类似于统计中的参数和非参数方法的分类。基于参数或基于模型的方法假定已知的分布/模型（例如高斯）以获得推断，而非参数或无模型方法假设没有基础分布/模型并且使用经验分布获得推断。

 

二. 纤维重建算法介绍

1. Model-based methods

基于模型的方法包括DTI，球棍模型，NODDI以及更复杂的模型，如CHARM和AxCaliber。

基于模型的方法假设特定的扩散分布模式/函数（前面提到的N阶方程），将扩散信号与模型拟合来计算参数。

DTI假设水扩散速度遵循3D高斯分布，并且计算的张量恰好是高斯的协方差矩阵。

球棍模型是一种多张量模型，而球是各向同性高斯，棒是纯各向异性高斯。

其他的模型方法则是引入更复杂的扩散方向模型进行运算。

与统计学中的参数方法类似，基于模型的方法的优势在于它们仅需要很少的样本来获得整个分布（如DTI，最少只需要6个扩散方向的影像就可以）。然而，基于模型的方法的结果会受到模型的限制，然而真实的扩散模式并不遵循该假设。而过于复杂的模型也可能具有过拟合问题（利用大于N的扩散影像数据，来计算N阶函数），例如过去的研究使用双指数模型来拟合细胞内和细胞外扩散，但事实证明它们未能揭示这种生物物理学。

还有其他方法同时属于两种方法，如球形反卷积方法（包括CSD和其他衍生方法）可以被视为基于模型的方法，因为它们假定纤维群的基础分布（即响应函数，response function）并将其用于反卷积。它也可以被视为无模型，因为它们也获得了纤维分布的ODF（也称为纤维取向分布，FOD，如下图）。这些方法的优点在于它们具有基于模型和无模型方法的优点，即较少的采样以获得尖锐的ODF）；缺点是模型不真实，对异常值敏感，容易产生假纤维），如果存在模型不匹配，CSD会产生假的交叉纤维（Parker，GD，Neuroimage 65：433-448。，2013，Schilling，K.，Neuroimage 129：185-197.2016）并且跟踪结果可能是嘈杂的。

 

2. Model-free methods

无模型方法估计水扩散的经验分布，不施加对分布的假设，包括扩散光谱成像（DSI），Q ball成像（QBI）和广义q-采样成像（GQI）。

DSI使用傅里叶变换和数值积分来计算水扩散的方向分布函数（ODF，不同方向的水扩散的经验分布）。傅里叶变换需要特定的grid  diffusion sampling（多个b值，多个方向）。

QBI使用Funk-Randon变换或球谐函数来计算ODF。该计算需要shell-like diffusion sampling scheme（即HARDI采集，单个b值，多个方向）。 GQI提供了扩散信号和自旋分布函数（SDF）之间的关系，可以应用于任何扩散影像。 SDF是不同方向的水扩散密度，是一种扩散ODF。该关系允许GQI直接计算SDF，从而避免数值估计中的误差。

无模型方法的优点是它们不受模型的限制。它们不假设特定的扩散结构，并且没有违反模型的风险。没有基于模型的方法的过拟合问题。计算不需要复杂的优化或拟合，因此与基于模型的方法相比，受异常值的影响较小。无模型方法的缺点是它们通常需要更多的扩散采样，至少需要60个方向的数据才能获得更稳健的估计（相比之下，除了b0之外，DTI只需要6次采样）。

如果您正在使用DSI或QBI重建，不妨换成GQI，原因如下：

（1）GQI的数学计算更准确：DSI和QBI仅提供扩散ODF的数值估计，而GQI提供扩散ODF的直接分析关系（此处称为SDF）。在DSI中，数值估计包括傅立叶变换，接着是用于去除噪声的滤波器和用数值插值的径向积分。在QBI中，数值估计包括在Funk-Randon变换之前在径向方向上的重新样本扩散，或者使用球形分解来估计球谐函数以在将其转换回ODF之前计算变换。在GQI中，由于提供了分析关系，因此计算不是数值估计，而是使用简单矩阵乘法将扩散信号转换为SDF的直接计算。 

（2）GQI适用的数据类型更广泛：DSI仅适用于网格数据grid  diffusion sampling（多个b值，多个方向），QBI仅适用于shell数据（单个b值，多个方向），但GQI可应用于grid，shell，multi-shell和非grid非shell数据。

（3）GQI还可以在T1W空间或MNI空间中重建数据，这种衍生方法称为QSDR，这是一种直接在MNI空间中重建扩散模式的方法，因此可以用于组比较和回归研究（基于群体的模板）。 QSDR支持模板构建，连接组指纹识别和连接测量分析。从GQI计算的SDF还提供基于密度的测量，例如QA，ISO和RDI，它与ODF不同，ODF是单位球面上的概率密度函数。

 

三. 纤维重建算法的选择

方法的选择实际上取决于应用以及图像数据的信噪比和采集方式。如果数据质量非常好（良好的SNR），基于模型的复杂方法（如球棒模型，NODDI或CSD）可以很好地工作（CSD仅适用于shell数据）。如果数据有噪声，更好的选择是DTI或GQI。最近的一项比较研究表明，准确率最高的方法是GQI和DTI（https://www.nature.com/articles/s41467-017-01285-x），不过这是因为文献中使用数据的SNR较差。

我个人选择的方法是GQI，QSDR和DTI。原因在于我个人对统计数据的偏好：如果有一个未知的分布，我要做的第一件事是用高斯拟合，看看它的均值和标准差，这与DTI类似（DTI所做的是使用3D高斯模型拟合数据）。简单的高斯拟合将对噪声具有鲁棒性，即使数据样本有限，我们也可以看到整体分布模式。如果我有足够的数据样本，那么我将计算经验分布（empirical distribution）以观察未知分布的整体模式，这与GQI观察扩散的经验分布相同，经验分布将忠实地揭示扩散模式，并且不会偏向模型假设或仅仅由于模型不匹配而给出错误估计。尽管无模型方法长期以来一直曾被批评，但随着多波段采集（multi band）的进展使我们能够在短扫描时间内获得大量的扩散采样，快速成像的发展就可以支持无模型方法的应用场景。

 

注：本文第二、三部分译自DSIStudio图像重建方法介绍 http://dsi-studio.labsolver.org/Manual/Reconstruction，可以进入链接查看各种算法的数学计算和MATLAB实现程序