论文阅读 GA-Net: Guided Aggregation Net for End-to-end Stereo Matching
本论文是CVPR2019收录的文章。
论文链接:https://arxiv.org/pdf/1904.06587v1.pdf
GitHub链接:https://github.com/feihuzhang/GANet
摘要
在立体匹配任务中,为了准确估计视差,代价聚合在传统方法和深层神经网络模型中都是至关重要的。我们提出了两个新的神经网络层,分别用于捕获局部和整个图像的成本相关性。第一个是半全局聚合层(SGA),它是半全局匹配(SGM)的可微近似;第二个是局部引导聚合层(LGA),它遵循传统的成本过滤策略(Cost filter)来细化薄结构。
这两层可以用来代替广泛使用的耗费大量体积和内存的3D卷积层。
在实验中,我们发现具有两层引导聚集块的网络比具有19个3D卷积层的GC-NET更好。我们还训练了一个深度引导聚合网络(GA-NET),该网络在Scene Flow dataset和KITTI基准上比最先进的方法获得更高的精度。
创新点
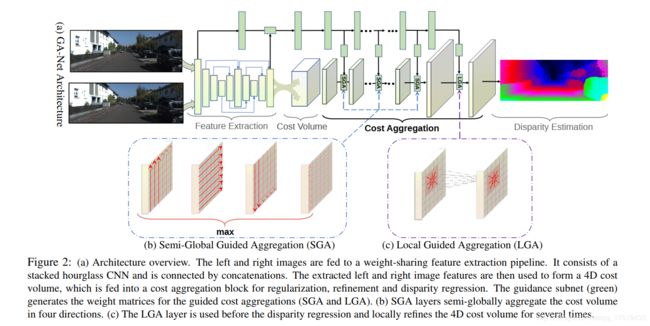
GA-Net借鉴了大量GC-Net和传统的SGM 中的内容,主要的创新之处在于提出了一个代价聚合网络,其中包含两种代价聚合层: Semi-Global Aggregation (半全局聚合) 和 local guided aggregation (局部引导聚合)。
其中SGA是借鉴了SGM的思想,用于处理由于遮挡,平滑,反射,噪声造成的错误匹配。
LGA则是借鉴了Cost filter的思想,用于处理由于下采样和上采样过程中造成的边缘模糊或者是薄结构模糊。
相关工作
Local Cost Aggregation
本文的LGA借鉴于此。
C A ( p , d ) = ∑ q ∈ N p ω ( p , q ) ⋅ C ( q , d ) C^{A}(\mathbf{p}, d)=\sum_{\mathbf{q} \in N_{\mathrm{p}}} \omega(\mathbf{p}, \mathbf{q}) \cdot C(\mathbf{q}, d) CA(p,d)=q∈Np∑ω(p,q)⋅C(q,d)
其中引导滤波权重w可以根据不同的图像滤波来获得。
Semi-Global Matching
经典的SGM算法,SGM 算法主要做出了两个贡献:1)提出了基于互信息的匹配代价计算方式 2)提出了一种半全局的代价聚合方式
本文借鉴了其半全局的代价聚合方式。
立体匹配可以看作是通过最小化能量函数E(D)来寻找最优的视差图D
E ( D ) = Σ p { C p ( D p ) + ∑ q ∈ N p P 1 ⋅ δ ( ∣ D p − D q ∣ = 1 ) + ∑ q ∈ N p P 2 ⋅ δ ( ∣ D p − D q ∣ > 1 ) } ( 3 ) \begin{aligned} E(D)=\Sigma_{\mathbf{p}}\left\{C_{\mathbf{p}}\left(D_{\mathbf{p}}\right)\right.&+\sum_{\mathbf{q} \in N_{\mathbf{p}}} P_{1} \cdot \boldsymbol{\delta}\left(\left|D_{\mathbf{p}}-D_{\mathbf{q}}\right|=1\right) \\ &\left.+\sum_{\mathbf{q} \in N_{\mathbf{p}}} P_{2} \cdot \boldsymbol{\delta}\left(\left|D_{\mathbf{p}}-D_{\mathbf{q}}\right|>1\right)\right\} (3)\end{aligned} E(D)=Σp{Cp(Dp)+q∈Np∑P1⋅δ(∣Dp−Dq∣=1)+q∈Np∑P2⋅δ(∣Dp−Dq∣>1)⎭⎬⎫(3)
其中,C为匹配代价,公式的第一项是数据项,表示当视差图为D时,所有像素的匹配代价的累加,第二项和第三项是平滑项,表示对像素p的Np邻域内的所有像素q进行惩罚,其中第二项惩罚力度较小(P1较小),对相邻像素视差变化很小的情况(1个像素)进行惩罚;第二项惩罚力度较大(P2> P1),对相邻像素视差变化很大(大于1个像素)的情况进行惩罚。较小的惩罚项可以让算法能够适应视差变化小的情形,如倾斜的平面或者连续的曲面,较大的惩罚项可以让算法正确处理视差非连续情况。于影像灰度边缘处视差非连续的可能性较大,为了保护真实场景中的视差非连续情况,P2往往是根据相邻像素的灰度差来动态调整。调整公式如下:
P 2 = P 2 ′ ∣ I b p − I b q ∣ , P 2 > P 1 P_{2}=\frac{P_{2}^{\prime}}{\left|I_{b p}-I_{b q}\right|}, \quad P_{2}>P_{1} P2=∣Ibp−Ibq∣P2′,P2>P1
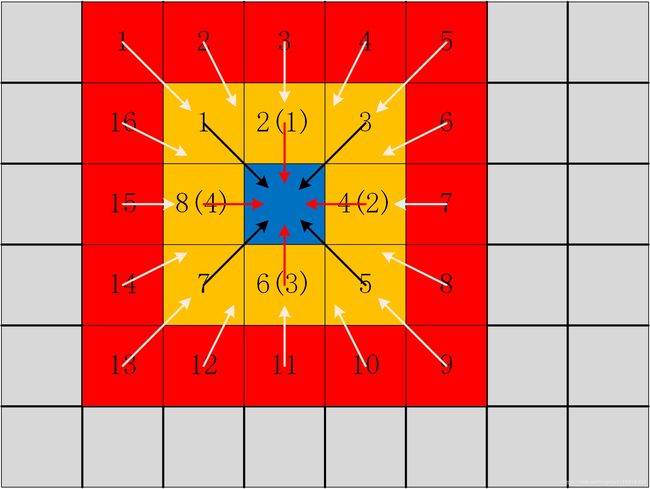
但是求解这个E是个NP完全问题,所以SGM提出了一种路径代价聚合的方法,即将像素所有视差下的匹配代价进行像素周围所有路径上的一维聚合得到路径下的路径代价值,然后将所有路径代价值相加得到该像素聚合后的匹配代价值。下面的式子是当视差为d时,位置p在整张图像中从方向r上的聚合代价
C r A ( p , d ) = C ( p , d ) + min { C r A ( p − r , d ) C r A ( p − r , d − 1 ) + P 1 C r A ( p − r , d + 1 ) + P 1 min C r A ( p − r , i ) + P 2 C_{\mathrm{r}}^{\mathrm{A}}(\mathbf{p}, d)=C(\mathbf{p}, d)+\min \left\{\begin{array}{c}{C_{\mathrm{r}}^{\mathrm{A}}(\mathbf{p}-\mathbf{r}, d)} \\ {C_{\mathrm{r}}^{\mathrm{A}}(\mathbf{p}-\mathbf{r}, d-1)+P_{1}} \\ {C_{\mathrm{r}}^{\mathrm{A}}(\mathbf{p}-\mathbf{r}, d+1)+P_{1}} \\ {\min C_{\mathrm{r}}^{\mathrm{A}}(\mathbf{p}-\mathbf{r}, i)+P_{2}}\end{array}\right. CrA(p,d)=C(p,d)+min⎩⎪⎪⎨⎪⎪⎧CrA(p−r,d)CrA(p−r,d−1)+P1CrA(p−r,d+1)+P1minCrA(p−r,i)+P2
其中,第一项为匹配代价值C,属于数据项;第二项是平滑项,表示的是和式2相同的含义,累加到路径代价上的值取不做惩罚、做P1惩罚和做P2惩罚三种情况中代价最小的值。
这个最小值是从4种可能的候选值中选取的最小值:
1.前一个像素(左相邻像素)disparity取值为d时,其最小的cost值。
2.前一个像素(左相邻像素)disparity取值为d-1时,其最小的cost值+惩罚系数P1。
3.前一个像素(左相邻像素)disparity取值为d+1时,其最小的cost值+惩罚系数P1。
4.前一个像素(左相邻像素)disparity取值为其他时,其最小的cost值+惩罚系数P2。
路径聚合示意图:
GA-NET 创新
Semi-Global Aggregation(SGA)半全局聚合
传统SGM算法应用在神经网络中存在的困难
传统的SGM算法从不同的方向迭代的聚合匹配代价。但是在端到端可训练的深度神经网络中应用这种方法存在一些困难:
- SGM有许多用户自定义的参数(P1,P2),很难调优。这些参数在神经网络训练过程中都成为不稳定因素;
- SGM对所有像素、区域和图像的代价聚合和惩罚是固定的,不适应不同的条件;
- 在深度估计中,硬最小值选择会导致大量的前向平行曲面。
所以GA-NET提出了一种可以用于端到端神经网络的类SGM算法:SGA,公式如下
C r A ( p , d ) = C ( p , d ) + sum { w 1 ( p , r ) ⋅ C r A ( p − r , d ) w 2 ( p , r ) ⋅ C r A ( p − r , d − 1 ) w 3 ( p , r ) ⋅ C r A ( p − r , d + 1 ) w 4 ( p , r ) ⋅ max i C r A ( p − r , i ) C_{\mathbf{r}}^{A}(\mathbf{p}, d)=C(\mathbf{p}, d) +\operatorname{sum}\left\{\begin{array}{l}{\mathbf{w}_{1}(\mathbf{p}, \mathbf{r}) \cdot C_{\mathbf{r}}^{A}(\mathbf{p}-\mathbf{r}, d)} \\ {\mathbf{w}_{2}(\mathbf{p}, \mathbf{r}) \cdot C_{\mathbf{r}}^{A}(\mathbf{p}-\mathbf{r}, d-1)} \\ {\mathbf{w}_{3}(\mathbf{p}, \mathbf{r}) \cdot C_{\mathbf{r}}^{A}(\mathbf{p}-\mathbf{r}, d+1)} \\ {\mathbf{w}_{4}(\mathbf{p}, \mathbf{r}) \cdot \max _{i} C_{\mathbf{r}}^{A}(\mathbf{p}-\mathbf{r}, i)}\end{array}\right. CrA(p,d)=C(p,d)+sum⎩⎪⎪⎨⎪⎪⎧w1(p,r)⋅CrA(p−r,d)w2(p,r)⋅CrA(p−r,d−1)w3(p,r)⋅CrA(p−r,d+1)w4(p,r)⋅maxiCrA(p−r,i)
和SGM有三种不同:
- 参数可学习,并将它们添加为匹配代价项的惩罚系数/权重。因此,对于不同的情况,这些权重在不同位置是自适应的并且更灵活。
- 我们用加权和替换SGM中的第一个/外部最小选择。
- 内部/第二最小选择被改变为最大值。这是因为我们模型中的学习目标是最大化 ground truth 深度的概率,而不是最小化匹配代价。由于方程中的 max i C r A ( p − r , i ) \max _{i} C_{\mathbf{r}}^{A}(\mathbf{p}-\mathbf{r}, i) maxiCrA(p−r,i)可以由d个不同的位置共享,这里,我们不使用另一个加权求和来替换它以便减少 计算复杂性。
为了防止 C r A ( p , d ) C_{\mathbf{r}}^{A}(\mathbf{p}, d) CrA(p,d)过大 ,使用归一化的参数:
s.t. ∑ i = 0 , 1 , 2 , 3 , 4 w i ( p , r ) = 1 \text { s.t. } \quad \sum_{i=0,1,2,3,4} \mathbf{w}_{i}(\mathbf{p}, \mathbf{r})=1 s.t. i=0,1,2,3,4∑wi(p,r)=1
其中C(p,d)就是Cost Volume 大小是(H ×W ×Dmax × F) 。Cost Volume被切片成Dmax块的三维块,用于计算他在深度d时的聚合代价。所用的权重W0W4在不同深度间是共享的。W0W4是由一个引导子网络获得的。与原始SGM在16个方向上进行聚合不同,为了提高效率,建议的聚合是沿着整个图像的每一行或每一列在总共四个方向(左,右,上和下)进行的,即 r ∈ { ( 0 , 1 ) , ( 0 , − 1 ) , ( 1 , 0 ) , ( − 1 , 0 ) } \mathbf{r} \in\{(0,1),(0,-1),(1,0),(-1,0)\} r∈{(0,1),(0,−1),(1,0),(−1,0)}
最后的聚合Cost Volume是选择四个方向的代价聚合后最大的那个Cost Volume:
C A ( p , d ) = max r C r A ( p , d ) C^{A}(\mathbf{p}, d)=\max _{\mathbf{r}} C_{\mathbf{r}}^{A}(\mathbf{p}, d) CA(p,d)=rmaxCrA(p,d)
最后的最大选择仅从一个方向保留最佳消息。这保证了聚集效应不会被其他方向所模糊。
这里不太清楚 ,为什么要选取最大的那一个?如何判断他是最大的那个?
从损失函数来看 ,Cost Volume的值应该是负的,这是他选取最大值的原因吗?
Local Guided Aggregation
局部引导聚合,目的在于细化薄结构和物体边缘。下采样和上采样在立体匹配模型中广泛使用,但是它模糊了薄的结构和对象边缘。 LGA层学习了几种引导滤波器,以优化匹配成本并帮助恢复薄结构信息。公式如下:
C A ( p , d ) = sum { ∑ q ∈ N p ω 0 ( p , q ) ⋅ C ( q , d ) ∑ q ∈ N p ω 1 ( p , q ) ⋅ C ( q , d − 1 ) ∑ q ∈ N p ω 2 ( p , q ) ⋅ C ( q , d + 1 ) s.t. ∑ q ∈ N p ω 0 ( p , q ) + ω 1 ( p , q ) + ω 2 ( p , q ) = 1 \begin{aligned} C^{A}(\mathbf{p}, d)=\operatorname{sum}\left\{\begin{array}{l}{\sum_{\mathbf{q} \in N_{\mathbf{p}}} \omega_{0}(\mathbf{p}, \mathbf{q}) \cdot C(\mathbf{q}, d)} \\ {\sum_{\mathbf{q} \in N_{\mathbf{p}}} \omega_{1}(\mathbf{p}, \mathbf{q}) \cdot C(\mathbf{q}, d-1)} \\ {\sum_{\mathbf{q} \in N_{\mathbf{p}}} \omega_{2}(\mathbf{p}, \mathbf{q}) \cdot C(\mathbf{q}, d+1)}\end{array}\right.\\ \text { s.t. } \sum_{\mathbf{q} \in N_{\mathbf{p}}} \omega_{0}(\mathbf{p}, \mathbf{q})+\omega_{1}(\mathbf{p}, \mathbf{q})+\omega_{2}(\mathbf{p}, \mathbf{q})=1 \end{aligned} CA(p,d)=sum⎩⎪⎨⎪⎧∑q∈Npω0(p,q)⋅C(q,d)∑q∈Npω1(p,q)⋅C(q,d−1)∑q∈Npω2(p,q)⋅C(q,d+1) s.t. q∈Np∑ω0(p,q)+ω1(p,q)+ω2(p,q)=1
Cost Volume的不同切片(总计Dmax切片)在LGA中共享相同的过滤/聚合权重。
LGA和传统的代价滤波的不同之处
-
传统的代价滤波方法在K×K局部/周围区域Np中采用K×K的滤波核去过滤代价值
-
LGA层在每个像素位置p上拥有三个K×K的滤波(w0,w1,w2),分别是针对于视差d,d-1,d+1。也就是说,在每个像素位置p的K×K的局部区域中,LGA采用K×K×3的权重矩阵进行聚合。
高效实施
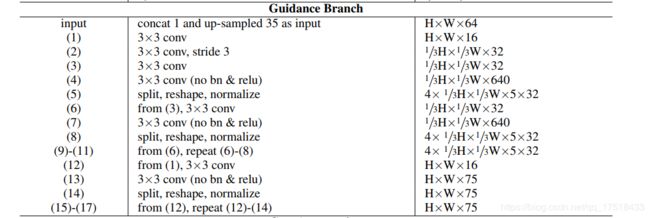
引导子网络
GA-Net采用几个2D卷积层去构建一个快速的引导子网络(如网络框架中所示)。其输入是左右图、feature map,输出是聚合权重w。
引导子网络的参数量变化:
对于一个大小为H×W×D×F(D是最大视差,F是feature size)的4D代价值C而言:
- SGA:将引导子网络的输出分割、变形和归一化为四个H×W×K×F权重矩阵,用于进行四个方向的SGA。注意:此处的K是公式中的w0~w4这5个参数,所以K=5
- LGA:需要学习一个H×W×3K^2×F(K=5)的权重矩阵,然后使用公式进行LGA聚合。
并行
即使SGA层涉及整个宽度或高度上的迭代聚合,由于不同要素通道或行/列中元素之间的独立性,可以并行计算前向和后向。例如,在向左方向聚合时,不同通道或行中的元素是独立的,可以同时计算。通过简单地将LGA层的元素分解为逐元素矩阵的乘法和求和,也可以并行计算。
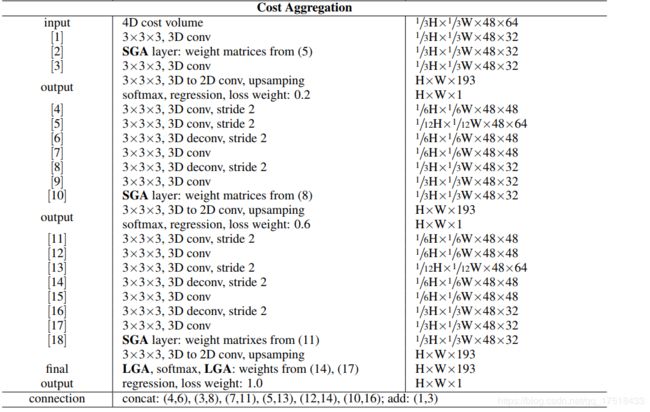
网络结构
GA-Net包含四个部分:
-
特征提取块:一个堆叠的沙漏网络。左右视角图共享该特征提取块。
-
对四维代价值的代价聚合:采用几个SGA层用于代价聚合。LGA层执行在视差回归的softmax层的前面和后面。
-
引导子网络:生成代价聚合权重
-
视差回归:softmax层
损失函数
L ( d ^ , d ) = 1 N ∑ n = 1 N l ( ∣ d ^ − d ∣ ) l ( x ) = { x − 0.5 , x ≥ 1 x 2 / 2 , x < 1 \begin{aligned} L(\hat{d}, d) &=\frac{1}{N} \sum_{n=1}^{N} l(|\hat{d}-d|) \\ l(x) &=\left\{\begin{array}{ll}{x-0.5,} & {x \geq 1} \\ {x^{2} / 2,} & {x<1}\end{array}\right.\end{aligned} L(d^,d)l(x)=N1n=1∑Nl(∣d^−d∣)={x−0.5,x2/2,x≥1x<1
使用L1距离,因为作者觉得与L2损失相比,平滑L1在视差不连续时具有鲁棒性,并且对异常值或噪声的敏感性较低。
d ^ = ∑ d = 0 D max d × σ ( − C A ( d ) ) \hat{d}=\sum_{d=0}^{D_{\max }} d \times \sigma\left(-C^{A}(d)\right) d^=d=0∑Dmaxd×σ(−CA(d))
视差预测dˆ是每个视差候选者的总和,按其概率加权。在通过softmax操作进行成本汇总之后,计算每个视差d的概率。与基于分类的方法相比,视差回归显示出更强大的功能,并且可以产生亚像素精度。
实验

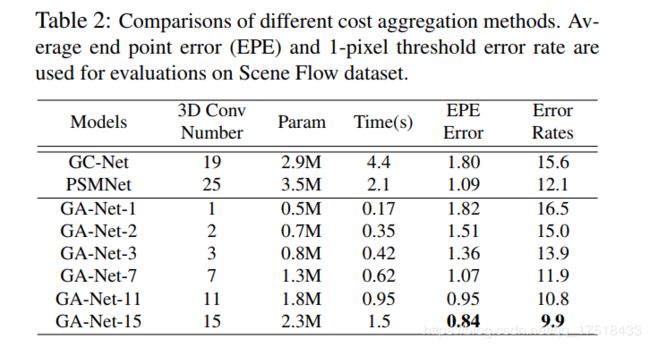
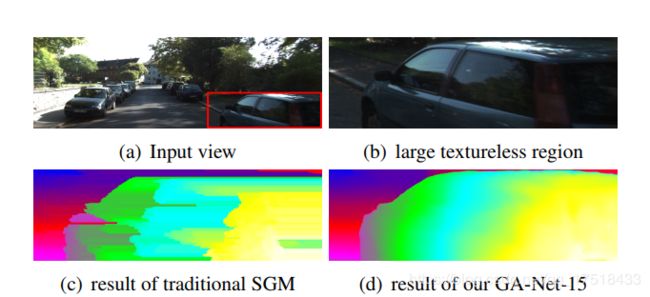
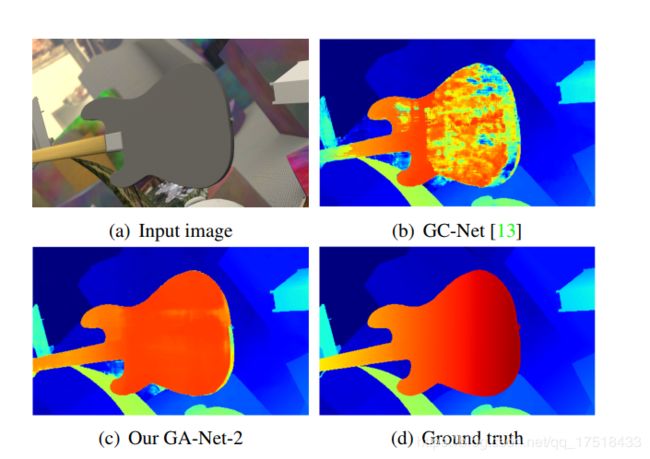
GA-Net以最少的网络层数取得了优于GC-Net和PSMNet的正确率。

对于大范围无纹理区域、反射区域和物体边缘的深度概率预测,代价聚合层起到了明显的效果。