隐马尔科夫模型（HMM）笔记（公式+代码）

隐马尔科夫模型（hidden Markov model，HMM）是可用于 标注问题的统计学习模型，描述由隐藏的马尔可夫链随机生成观测序列的过程，属于生成模型。隐马尔可夫模型在语音识别、自然语言处理、生物信息、模式识别等领域有着广泛的应用。

本文内容部分引用于 李航《统计学习方法》

1. 基本概念

1.1 HMM模型定义

• 隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测从而产生观测随机序列的过程。
• 隐藏的马尔可夫链随机生成的状态的序列，称为状态序列（state sequence）；
• 每个状态生成一个观测，而由此产生的观测的随机序列，称为观测序列（observation sequence）。
• 序列的每一个位置又可以看作是一个时刻。

一个不一定恰当的例子：你只知道一个人今天是散步了，逛街了，还是在家打扫卫生，推测今天的天气；这个人在下雨天可能在家打扫卫生，也有可能雨中散步，晴天可能去逛街，也有可能散步，或者打扫卫生
隐藏状态 Y（不可见）：下雨，晴天
观察状态 X（可见）： 散步，逛街，打扫房间

假设我们观测到的状态是$X$序列，$X=(x_1,x_2,x_3,...x_n)$, 隐藏状态是$Y$序列，$Y=(y_1,y_2,y_3,...y_n)$

我们在知道观测序列$X$的情况下，求有多大概率是该隐藏状态序列$Y$

• 贝叶斯公式 $P(B|A)=\frac{P(AB)}{P(A)}=\frac{P(A|B)P(B)}{P(A)}$

现在我们要求的就是$P(Y|X)$
$$\begin{array}{rl}P(Y|X)& =P(y_1,y_2,y_3,\cdots ,y_n|x_1,x_2,x_3,\cdots ,x_n)\\ & =\frac{P(x_1,x_2,x_3,\cdots ,x_n|y_1,y_2,y_3,\cdots ,y_n)P(y_1,y_2,y_3,\cdots ,y_n)}{P(x_1,x_2,x_3,\cdots ,x_n)}(0)\\ P(y_1,y_2,y_3,\cdots ,y_n)& =P(y_1)P(y_2,y_3,y_4,\cdots ,y_n|y_1)\\ & =P(y_1)P(y_2|y_1)P(y_3,y_4,\cdots ,y_n|y_1,y_2)\\ & =P(y_1)P(y_2|y_1)P(y_3|y_1,y_2)P(y_4,\cdots ,y_n|y_1,y_2,y_3)\\ ⋮& \\ & =P(y_1)P(y_2|y_1)P(y_3|y_1,y_2)\cdots P(y_{n-1}|y_1,y_2,\cdots ,y_{n-2})P(y_n|y_1,y_2,\cdots ,y_{n-1})\\ & =P(y_1)\prod _{i=2}^{n}P(y_i|y_1,y_2,y_3,\cdots ,y_{i-1})\\ & =P(y_1)\prod _{i=2}^{n}P(y_i|y_{i-1})(1)\end{array}$$

隐马尔可夫模型 两个假设

• 上式最后一步是隐马尔可夫的 齐次性 假设：当前状态 $y_i$ 仅依赖于前一个状态 $y_{i-1}$
• 下面式子最后一步是隐马尔可夫的 观测独立性 假设：观测值 $x_i$ 只跟他的隐含状态 $y_i$ 相关

$$\begin{array}{rl}& P(x_1,x_2,x_3,\cdots ,x_n|y_1,y_2,y_3,\cdots ,y_n)\\ =& \prod _{i=1}^{n}P(x_i|x_1,x_2,x_3,\cdots ,x_{i-1},y_1,y_2,y_3,\cdots ,y_n)\\ =& \prod _{i=1}^{n}P(x_i|y_i)(2)\end{array}$$

• 由$(1)(2)$, 且$(0)$式忽略分母
  $$\begin{array}{rl}P(Y|X)=& P(y_1,y_2,y_3,\cdots ,y_n|x_1,x_2,x_3,\cdots ,x_n)\\ =& \frac{P(x_1,x_2,x_3,\cdots ,x_n|y_1,y_2,y_3,\cdots ,y_n)P(y_1,y_2,y_3,\cdots ,y_n)}{P(x_1,x_2,x_3,\cdots ,x_n)}\\ \propto & P(y_1)\prod _{i=2}^{n}P(y_i|y_{i-1})\prod _{i=1}^{n}P(x_i|y_i)\end{array}$$

隐马尔可夫模型由 三要素 决定

• 初始状态概率向量 $\pi$,（初始处于各个隐藏状态 $y_i$ 的概率）
• 状态转移概率矩阵 $A$,（即式（1）中的 $P(y_i|y_{i-1})$ 的各种项构成的矩阵）
• 观测概率矩阵 $B$, （即式（2）中的 $P(x_i|y_i)$ 的各种项构成的矩阵）

$\pi$ 和 $A$ 决定状态序列，$B$ 决定观测序列。隐马尔可夫模型 $\lambda$ 可以用三元符号表示，$\lambda =（A，B，\pi ）$

• 状态转移概率矩阵 $A$ 与 初始状态概率向量 $\pi$ 确定了隐藏的马尔可夫链，生成不可观测的状态序列。
• 观测概率矩阵 $B$ 确定了如何从隐藏状态 $y_i$ 生成观测 $x_i$，与状态序列综合确定了如何产生观测序列。

1.2 盒子和球模型

假设有4个盒子，每个盒子里都装有红、白两种颜色的球，盒子里的红、白球数由表列出。

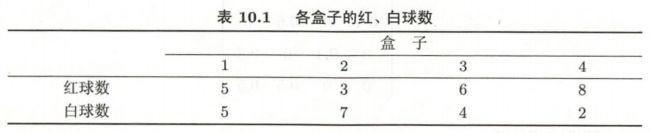
按下面的方法抽球，产生一个球的颜色的观测序列 $X$：

• 等概率随机选1个盒子，从这个盒子里随机抽出1个球，记录颜色，放回；
• 从当前盒子随机转移到下一个盒子，规则是：如果当前盒子是盒子1，那么下一盒子一定是盒子2；如果当前是盒子2或3，那么分别以概率0.4和0.6转移到左边或右边的盒子；如果当前是盒子4，那么各以0.5的概率停留在盒子4或转移到盒子3；
• 确定转移的盒子后，再从这个盒子里随机抽出1个球，记录颜色，放回；
• 重复5次，得到一个球的颜色的观测序列
  
• 各个隐含状态的初始概率 $P(y_i)$ ： $\pi =(0.25,0.25,0.25,0.25{)}^T$
• 各个隐含状态间的转移概率 $P(y_i|y_{i-1})$ ： $A=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0.4& 0& 0.6& 0\\ 0& 0.4& 0& 0.6\\ 0& 0& 0.5& 0.5\end{array}\right]$
• 观测(发射)概率 $P(x_i|y_i)$：$B=\left[\begin{array}{cc}0.5& 0.5\\ 0.3& 0.7\\ 0.6& 0.4\\ 0.8& 0.2\end{array}\right]$

1.3 观测序列生成过程

• 输入：隐马模型 $\lambda =（A，B，\pi ）$，观测序列长度 $T$ (该例子为 5)
• 输出：观测序列 $X=(x_1,x_2,x_3,x_4,x_5)$ , (红、白球)

1. 跟据 $\pi$ 随机产生一个 $y_i$ 状态(盒子), 序列长度 t = 0
2. 在 $y_i$ 中，按照其观测概率 $B$ 对应的行，产生一个观测序列 $X$ 的元素 $x_i$（红球 or 白球），计数 t++
3. 根据 $y_i$ 的状态转移概率 $A$ 对应的行，产生下一个状态 $y_{i+1}$ , while(t < T), 重复2,3步骤

1.4 HMM模型3个基本问题

1. 概率计算问题：给定模型 $\lambda =（A，B，\pi ）$ 和 观测序列 $X=(x_1,x_2.....,x_n)$, 计算在模型 $\lambda$ 下，观测序列 $X$ 出现的概率 $P(X|\lambda )$
2. 学习问题：已知观测序列 $X=(x_1,x_2.....,x_n)$，估计模型 $\lambda =（A，B，\pi ）$ 的参数，使得在该模型下，观测序列概率 $P(X|\lambda )$ 最大。极大似然估计的方法估计参数
3. 预测问题：也称解码(decoding)问题。已知模型 $\lambda =（A，B，\pi ）$ 和 观测序列 $X=(x_1,x_2.....,x_n)$，求对给定观测序列条件概率 $P(Y|X)$ 最大的状态序列 $Y=(y_1,y_2......,y_n)$。即给定观测序列 $X$，求最有可能的对应隐含状态序列 $Y$

2. 概率计算问题

给定模型 $\lambda =（A，B，\pi ）$ 和 观测序列 $X=(x_1,x_2.....,x_n)$, 计算在模型 $\lambda$ 下，观测序列 $X$ 出现的概率 $P(X|\lambda )$

2.1 直接计算法

• 列举所有的长度为 $T$ 的状态序列 $Y=(y_1,y_2......,y_t)$
• 求 各个 状态序列 $Y$ 与 观测序列 $X=(x_1,x_2.....,x_t)$ 的联合概率 $P(XY|\lambda )$
• 然后对上面所有的状态序列求和 $\Sigma$，得到 $P(X|\lambda )$

1. 状态序列 $Y=(y_1,y_2......,y_t)$ 的概率是：$P(Y|\lambda )={\pi }_{y_1}{A}_{y_1,y_2}{A}_{y_2,y_3}......A_{y_{t-1},y_t}$
2. 对固定的状态序列 $Y=(y_1,y_2......,y_t)$ ，观测序列 $X=(x_1,x_2.....,x_t)$ 的概率是：$P(X|Y,\lambda )=B_{y_1,x_1}{B}_{y_2,x_2}......B_{y_t,x_t}$
3. $X,Y$ 同时出现的联合概率为：$P(XY|\lambda )=P(X|Y,\lambda )P(Y|\lambda )={\pi }_{y_1}{B}_{y_1,x_1}{A}_{y_1,y_2}{B}_{y_2,x_2}......A_{y_{t-1},y_t}{B}_{y_t,x_t}$
4. 对上式在所有可能的状态序列 $Y_i$ 的情况下求和 $\Sigma$，即可得到 $P(X|\lambda )={\sum }_{Y_1}^{Y_n}P(X|Y,\lambda )P(Y|\lambda )$

但是上面计算量很大，复杂度 $O(T{N}^T)$，不可行

2.2 前向算法

• 前向概率 概念：
  给定HMM模型 $\lambda$，定义到时刻 t 部分观测序列 $X_{part}=(x_1,x_2.....,x_t)$ 且 t 时刻的状态 $y_t$ 为 $q_i$ 的概率为前向概率，记为：$a_t(i)=P(x_1,x_2,...,x_t,y_t=q_i|\lambda )$

• 递推求解 前向概率 $a_t(i)$ 及 观测序列概率 $P(X|\lambda )$

输入：给定HMM模型 $\lambda$, 观测序列 $X$
输出：观测序列概率 $P(X|\lambda )$

1. 初值： $a_1(i)={\pi }_i{B}_{i,x_1}i=1,2,...,N$ ，$N$ 为盒子个数
2. 递推：对 $t=1,2,...,T-1$，$a_{t+1}(i)=\left[\begin{array}{c}{\sum }_{j=1}^N{a}_t(j)A_{j,i}\end{array}\right]B_{i,x_{t+1}}i=1,2,...,N$
3. 终止： $P(X|\lambda )={\sum }_{i=1}^N{a}_T(i)$（看前向概率定义，全概率公式）

算法解释：

• 初始时刻 $t=1$，观测到的是 $x_1$, 可能的状态是盒子的编号 $i=1,2,...,N$，概率为 ${\pi }_i$，在 $i$ 盒子发射出 $x_1$ 颜色球的概率为 $B_{i,x_1}$，所以 $a_1(i)={\pi }_i{B}_{i,x_1}$

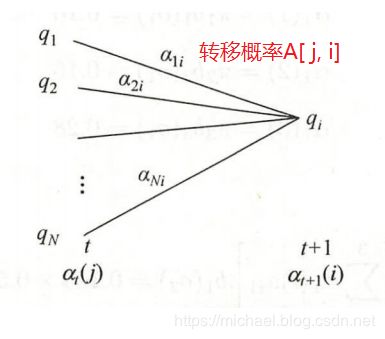
• 递推：上一时刻 $t$ 的 N 种情况下 都可能转移到 $t+1$ 时的 $q_i$ 状态，对应的前向概率乘以转移概率，并求和，得到 状态 $q_i$ 的概率，再乘以发射概率 $B_{i,x_{t+1}}$，就是 $t+1$ 时的前向概率
  

• 最后一个时刻 $T$ 时的所有前向概率求和就是 $P(X|\lambda )={\sum }_{i=1}^N{a}_T(i)$

• 前向算法是基于路径的，$t+1$ 时刻，直接用 $t$ 时刻的结果，时间复杂度 $O(T{N}^2)$
  

2.2.1 前向公式证明

首先有公式联合概率 $P(ABC)=P(A)P(B|A)P(C|AB)$,对任意多个项都成立
递推公式证明：
$$\begin{array}{rl}{a}_t(j)A_{j,i}& =P(x_1,x_2,...,x_t,y_t=q_j|\lambda )P(y_{t+1}=q_i|y_t=q_j,\lambda )\\ & =P(x_1,x_2,...,x_t|y_t=q_j,\lambda )P(y_t=q_j|\lambda )P(y_{t+1}=q_i|y_t=q_j,\lambda )\\ & =P(x_1,x_2,...,x_t|y_t=q_j,y_{t+1}=q_i,\lambda )P(y_t=q_j,y_{t+1}=q_i|\lambda )\\ & =P(x_1,x_2,...,x_t,y_t=q_j,y_{t+1}=q_i|\lambda )\\ \{\sum _{j=1}^N{a}_t(j)A_{j,i}\}{B}_{i,x_{t+1}}& =P(x_1,x_2,...,x_t,y_{t+1}=q_i|\lambda )P(x_{t+1}|y_{t+1}=q_i,\lambda )\\ & =P(x_1,x_2,...,x_t|y_{t+1}=q_i,\lambda )P(y_{t+1}=q_i|\lambda )P(x_{t+1}|y_{t+1}=q_i,\lambda )\\ & =P(x_1,x_2,...,x_t|y_{t+1}=q_i,x_{t+1},\lambda )P(x_{t+1},y_{t+1}=q_i|\lambda )\\ & =P(x_1,x_2,...,x_t,x_{t+1},y_{t+1}=q_i|\lambda )=a_{t+1}(i)\end{array}$$
第一个蓝色处：前 $t$ 个观测序列，显然跟 $t+1$ 时刻的状态 $y_{t+1}$无关，第二个蓝色处：观测独立性

终止公式证明(全概率公式)：
$$\begin{array}{rl}\sum _{i=1}^N{a}_T(i)& =P(x_1,x_2,...,x_T,y_T=q_1|\lambda )+P(x_1,x_2,...,x_T,y_T=q_2|\lambda )+P(x_1,x_2,...,x_T,y_T=q_N|\lambda )\\ & =P(x_1,x_2,...,x_T|\lambda )=P(X|\lambda )\end{array}$$

2.2.2 盒子和球例子

考虑盒子和球模型 $\lambda =(A,B,\pi )$，状态集合（盒子的编号）$Q=\{1,2,3\}$，观测集合 $V=\{红，白\}$
$$\pi =\left[\begin{array}{c}0.2\\ 0.4\\ 0.4\end{array}\right],A=\left[\begin{array}{ccc}0.5& 0.2& 0.3\\ 0.3& 0.5& 0.2\\ 0.2& 0.3& 0.5\end{array}\right],B=\left[\begin{array}{cc}0.5& 0.5\\ 0.4& 0.6\\ 0.7& 0.3\end{array}\right]$$
设总的时间长度 $T=3$, 观测序列 $X=(红，白，红)$，用前向算法计算 $P(X|\lambda )$

解 ：

1. 计算前向概率初值：$a_1(i)={\pi }_i{B}_{i,x_1}$
   $a_1(1)={\pi }_1{B}_{1,1}=0.2\ast 0.5=0.10$，（1号盒子，时刻1摸出红色(第一列)的概率）
   $a_1(2)={\pi }_2{B}_{2,1}=0.4\ast 0.4=0.16$，（2号盒子，时刻1摸出红色的概率）
   $a_1(3)={\pi }_3{B}_{3,1}=0.4\ast 0.7=0.28$，（3号盒子，时刻1摸出红色的概率）

2. 递推计算：对 $t=1,2,...,T-1$，$a_{t+1}(i)=\left[\begin{array}{c}{\sum }_{j=1}^N{a}_t(j)A_{j,i}\end{array}\right]B_{i,x_{t+1}}i=1,2,...,N$

$a_2(1)=\{{\sum }_{j=1}^3{a}_1(j)A_{j,1}\}{B}_{1,2}=(0.10\ast 0.5+0.16\ast 0.3+0.28\ast 0.2)\ast 0.5=0.077$
（时刻2时，从1号盒子摸出白色的概率）

$a_2(2)=\{{\sum }_{j=1}^3{a}_1(j)A_{j,2}\}{B}_{2,2}=(0.10\ast 0.2+0.16\ast 0.5+0.28\ast 0.3)\ast 0.6=0.1104$
（时刻2时，从2号盒子摸出白色的概率）

$a_2(3)=\{{\sum }_{j=1}^3{a}_1(j)A_{j,3}\}{B}_{3,2}=(0.10\ast 0.3+0.16\ast 0.2+0.28\ast 0.5)\ast 0.3=0.0606$
（时刻2时，从3号盒子摸出白色的概率）

---

$a_3(1)=\{{\sum }_{j=1}^3{a}_2(j)A_{j,1}\}{B}_{1,1}=(0.077\ast 0.5+0.1104\ast 0.3+0.0606\ast 0.2)\ast 0.5=0.04187$
（时刻3时，从1号盒子摸出红色的概率）

$a_3(2)=\{{\sum }_{j=1}^3{a}_2(j)A_{j,2}\}{B}_{2,1}=(0.077\ast 0.2+0.1104\ast 0.5+0.0606\ast 0.3)\ast 0.4=0.035512$
（时刻3时，从2号盒子摸出红色的概率）

$a_3(3)=\{{\sum }_{j=1}^3{a}_2(j)A_{j,3}\}{B}_{3,1}=(0.077\ast 0.3+0.1104\ast 0.2+0.0606\ast 0.5)\ast 0.7=0.052836$
（时刻3时，从3号盒子摸出红色的概率）

3. 终止：$P(X|\lambda )={\sum }_{i=1}^N{a}_T(i)={\sum }_{i=1}^3{a}_3(i)=0.04187+0.035512+0.052836=0.130218‬$

2.2.3 前向算法Python代码

• 借鉴他人代码，手敲一遍并理解

# -*- coding:utf-8 -*-
# python3.7
# @Time: 2019/12/17 22:33
# @Author: Michael Ming
# @Website: https://michael.blog.csdn.net/
# @File: hiddenMarkov.py
import numpy as np
class HiddenMarkov:
    def forward(self, Q, V, A, B, X, PI):   # 前向算法
        N = len(Q)  # 隐藏状态数量
        M = len(X)  # 观测序列大小
        alphas = np.zeros((N, M))   # 前向概率 alphas 矩阵
        T = M   # 时刻长度，即观测序列长度
        for t in range(T):  # 遍历每个时刻，计算前向概率 alphas
            indexOfXi = V.index(X[t])   # 观测值Xi对应的V中的索引
            for i in range(N):  # 对每个状态进行遍历
                if t == 0: # 计算初值
                    alphas[i][t] = PI[t][i] * B[i][indexOfXi]   # a1(i)=πi B(i,x1)
                    print("alphas1(%d)=p%dB%d(x1)=%f" %(i,i,i,alphas[i][t]))
                else:
                    alphas[i][t] = np.dot(
                        [alpha[t-1] for alpha in alphas],   #  取的alphas的t-1列
                        [a[i] for a in A]) *B[i][indexOfXi]    # 递推公式
                    print("alpha%d(%d)=[sigma alpha%d(i)ai%d]B%d(x%d)=%f"
                        %(t, i, t-1, i, i, t, alphas[i][t]))
                    print(alphas)
        P = sum(alpha[M-1] for alpha in alphas)  # 最后一列概率的和
        print("P=%f" % P)

Q = [1, 2, 3]
V = ['红', '白']
A = [[0.5, 0.2, 0.3], [0.3, 0.5, 0.2], [0.2, 0.3, 0.5]]
B = [[0.5, 0.5], [0.4, 0.6], [0.7, 0.3]]
# X = ['红', '白', '红', '红', '白', '红', '白', '白']
X = ['红', '白', '红']    # 书上的例子
PI = [[0.2, 0.4, 0.4]]

hmm = HiddenMarkov()
hmm.forward(Q, V, A, B, X, PI)

关于numpy的一些操作：

>>> a
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])
>>> b
array([[ 7,  8],
       [ 9, 10],
       [11, 12]])
>>> np.dot(a[0],[B[1] for B in b])
64
>>> np.dot([A[0] for A in a],[B[1] for B in b])
132
>>> np.multiply(a[0],[B[1] for B in b])
array([ 8, 20, 36])
>>> np.multiply([A[0] for A in a],[B[1] for B in b])
array([ 8, 40, 84])

运行结果：（跟上面计算一致）

alphas1(0)=p0B0(x1)=0.100000
alphas1(1)=p1B1(x1)=0.160000
alphas1(2)=p2B2(x1)=0.280000
alpha1(0)=[sigma alpha0(i)ai0]B0(x1)=0.077000
[[0.1   0.077 0.   ]
 [0.16  0.    0.   ]
 [0.28  0.    0.   ]]
alpha1(1)=[sigma alpha0(i)ai1]B1(x1)=0.110400
[[0.1    0.077  0.    ]
 [0.16   0.1104 0.    ]
 [0.28   0.     0.    ]]
alpha1(2)=[sigma alpha0(i)ai2]B2(x1)=0.060600
[[0.1    0.077  0.    ]
 [0.16   0.1104 0.    ]
 [0.28   0.0606 0.    ]]
alpha2(0)=[sigma alpha1(i)ai0]B0(x2)=0.041870
[[0.1     0.077   0.04187]
 [0.16    0.1104  0.     ]
 [0.28    0.0606  0.     ]]
alpha2(1)=[sigma alpha1(i)ai1]B1(x2)=0.035512
[[0.1      0.077    0.04187 ]
 [0.16     0.1104   0.035512]
 [0.28     0.0606   0.      ]]
alpha2(2)=[sigma alpha1(i)ai2]B2(x2)=0.052836
[[0.1      0.077    0.04187 ]
 [0.16     0.1104   0.035512]
 [0.28     0.0606   0.052836]]
P=0.130218

2.3 后向算法

• 后向概率 概念：
  给定HMM模型 $\lambda$，定义到时刻 $t$ 状态 $y_t$ 为 $q_i$ 的条件下，从 $t+1$ 到 $T$ 的部分观测序列 $X_{part}=(x_{t+1},x_{t+2}.....,x_T)$ 的概率为后向概率，记为：${\beta }_t(i)=P(x_{t+1},x_{t+2}.....,x_T|y_t=q_i,\lambda )$

• 递推求解 后向概率 ${\beta }_t(i)$ 及 观测序列概率 $P(X|\lambda )$

输入：给定HMM模型 $\lambda$, 观测序列 $X$
输出：观测序列概率 $P(X|\lambda )$

1. 初值： ${\beta }_T(i)=1i=1,2,...,N$ ，$N$ 为盒子个数
2. 递推：对 $t=T-1,T-2,...,1$，${\beta }_t(i)={\sum }_{j=1}^N{A}_{i,j}{B}_{j,x_{t+1}}{\beta }_{t+1}(j)i=1,2,...,N$
3. 终止： $P(X|\lambda )={\sum }_{i=1}^N{\pi }_i{B}_{i,x_1}{\beta }_1(i)$

算法解释：

2.3.1 后向公式证明

递推公式证明：
$$\begin{array}{rl}\sum _{j=1}^N{A}_{i,j}{B}_{j,x_{t+1}}{\beta }_{t+1}(j)& =\sum _{j=1}^N{A}_{i,j}P(x_{t+1}|y_{t+1}=q_j,\lambda )P(x_{t+2},...,x_T|y_{t+1}=q_j,\lambda )\\ & =\sum _{j=1}^N{A}_{i,j}P(x_{t+1}|x_{t+2},...,x_T,y_{t+1}=q_j,\lambda )P(x_{t+2},...,x_T|y_{t+1}=q_j,\lambda )\\ & =\sum _{j=1}^N{A}_{i,j}P(x_{t+1},x_{t+2},...,x_T|y_{t+1}=q_j,\lambda )\\ & =\sum _{j=1}^N{A}_{i,j}P(x_{t+1},x_{t+2},...,x_T|y_{t+1}=q_j,y_t=q_i,\lambda )\\ & =\sum _{j=1}^{N}P(y_{t+1}=q_j|y_t=q_i,\lambda )P(x_{t+1},x_{t+2},...,x_T|y_{t+1}=q_j,y_t=q_i,\lambda )\\ & =\sum _{j=1}^{N}P(x_{t+1},x_{t+2},...,x_T,y_{t+1}=q_j|y_t=q_i,\lambda )\\ & =P(x_{t+1},x_{t+2},...,x_T|y_t=q_i,\lambda )={\beta }_t(i)\end{array}$$
第一个蓝色处：观测独立性；第二个蓝色处：观测独立性（$x_{t+1},...x_T$都与$y_t$无关）

终止公式证明：
$$\begin{array}{rl}{\pi }_i{B}_{i,x_1}{\beta }_1(i)& =P(y_1=q_i|\lambda )P(x_1|y_1=q_i,\lambda )P(x_2,x_3,...,x_T|y_1=q_i,\lambda )\\ & =P(x_1,y_1=q_i|\lambda )P(x_2,x_3,...,x_T|x_1,y_1=q_i,\lambda )\\ & =P(x_1,x_2,...,x_T,y_1=q_i|\lambda )\\ \sum _{i=1}^N{\pi }_i{B}_{i,x_1}{\beta }_1(i)& =\sum _{i=1}^{N}P(x_1,x_2,...,x_T,y_1=q_i|\lambda )=P(x_1,x_2,...,x_T|\lambda )=P(X|\lambda )\end{array}$$

---

利用 前向 和 后向 概率的定义，可以将观测序列概率 $P(X|\lambda )$ 写成：
$P(X|\lambda )={\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_t(i)A_{i,j}{B}_{j,x_{t+1}}{\beta }_{t+1}(j),t=1,2,...,T-1$

证明如下：

$$\begin{array}{rl}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_t(i)A_{i,j}{B}_{j,x_{t+1}}{\beta }_{t+1}(j)& =\sum _{i=1}^N\sum _{j=1}^{N}P(x_1,x_2,...,x_t,y_t=q_i|\lambda )P(y_{t+1}=q_j|y_t=q_i,\lambda )\\ & \ast P(x_{t+1}|y_{t+1}=q_j,\lambda )P(x_{t+2},x_{t+3},...,x_T|y_{t+1}=q_j,\lambda )\\ & =\sum _{i=1}^N\sum _{j=1}^{N}P(x_1,x_2,...,x_t|y_t=q_i,\lambda )P(y_t=q_i|\lambda )P(y_{t+1}=q_j|y_t=q_i,\lambda )\\ & \ast P(x_{t+1}|x_{t+2},x_{t+3},...,x_T,y_{t+1}=q_j,\lambda )P(x_{t+2},x_{t+3},...,x_T|y_{t+1}=q_j,\lambda )\\ & =\sum _{i=1}^N\sum _{j=1}^{N}P(x_1,x_2,...,x_t|y_t=q_i,y_{t+1}=q_j,\lambda )P(y_t=q_i|\lambda )P(y_{t+1}=q_j|y_t=q_i,\lambda )\\ & \ast P(x_{t+1}|x_{t+2},x_{t+3},...,x_T,y_{t+1}=q_j,\lambda )P(x_{t+2},x_{t+3},...,x_T|y_{t+1}=q_j,\lambda )\\ & =\sum _{i=1}^N\sum _{j=1}^{N}P(x_1,x_2,...,x_t|y_t=q_i,y_{t+1}=q_j,\lambda )P(y_t=q_i|\lambda )P(y_{t+1}=q_j|y_t=q_i,\lambda )\\ & \ast P(x_{t+1},x_{t+2},x_{t+3},...,x_T|y_{t+1}=q_j,\lambda )\\ & =\sum _{i=1}^N\sum _{j=1}^{N}P(x_1,x_2,...,x_t,y_{t+1}=q_j|y_t=q_i,\lambda )P(y_t=q_i|\lambda )\\ & \ast P(x_{t+1},x_{t+2},x_{t+3},...,x_T|x_1,x_2,...,x_t,y_{t+1}=q_j,y_t=q_i,\lambda )\\ & =\sum _{i=1}^N\sum _{j=1}^{N}P(y_t=q_i|\lambda )P(x_1,x_2,...,x_t,y_{t+1}=q_j|y_t=q_i,\lambda )\\ & \ast P(x_{t+1},x_{t+2},x_{t+3},...,x_T|x_1,x_2,...,x_t,y_{t+1}=q_j,y_t=q_i,\lambda )\\ & =\sum _{i=1}^N\sum _{j=1}^{N}P(y_t=q_i|\lambda )P(x_1,x_2,...,x_t\\ & \\ & \\ & \end{array}$$