Java排序算法之插入排序
插入排序分为直接插入排序、折半插入排序、希尔排序,其中折半插入排序和希尔排序是优化后的插入排序,下面具体介绍着三种排序。
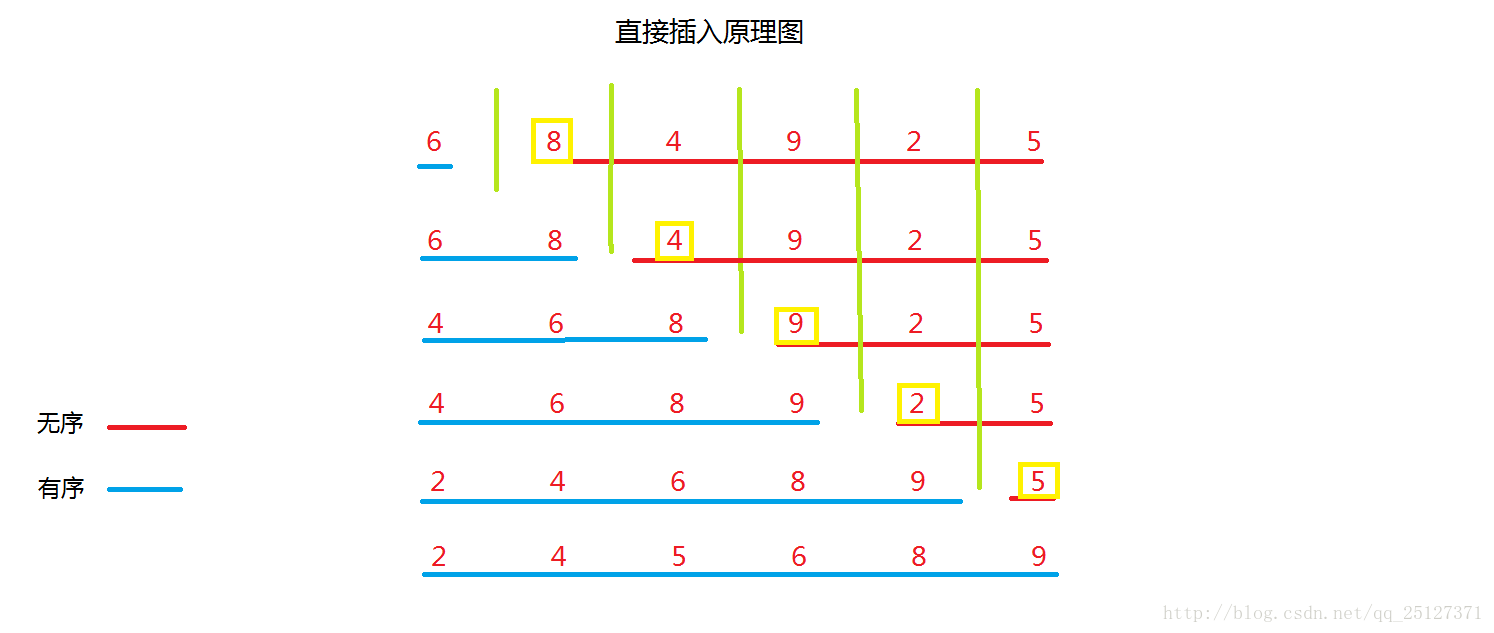
一、直接插入排序
1、算法思想 从序列的第i个元素为临界点,将序列分为有序序列和无序序列,即0~i-1为有序,i~n为无序。然后将i下标所对应的值复制一个备份为temp,然后用这个备份从后往前依次和前面的有序序列中的元素进行比较,直到遇见一个不大于temp的元素为止,然后从该索引处元素依次向后移,最后将备份的值赋给空出来的索引。3、Java代码实现
//直接插入排序
public static void insertSort(int arr[]) {
int target = 0;
int j = 0;
for (int i = 1; i < arr.length; i++) {
target = arr[i];
j = i;
while (j > 0 && target < arr[j - 1]) {
arr[j] = arr[j - 1];
j--;
}
arr[j] = target;
}
}
//测试
public static void main(String[] args) {
int arr[] = new int[] {1,3,6,9,7,2,8,5,4};
insertSort(arr);
System.out.println(Arrays.toString(arr));
}
结果:[1, 2, 3, 4, 5, 6, 7, 8, 9]
4、分析
时间复杂度为O(n^2),空间复杂度为O(1);当n比较小时(比如n<=50),并且记录规模较小时,直接插入排序较好。
二、折半法排序
1、算法思想:本质上是直接插入排序,只是无序序列中的元素依次和有序序列元素比较时利用折半法不断缩小比较范围,每次缩小序列1/2长度,具体实现是创建两个指针head和end分别指向有序序列的头和尾,计算出中间索引center的值,然后和无序序列取出的元素i进行比较,如果大于i,则应插入前半部分,将end指向center-1处,反之应在后半部分,将head指向center+1处。如果相等则为该索引,最后元素只需要后移找到的索引index到i-1之间的元素即可。
Java代码实现
public static void binarySort(int arr[]){
for(int i=1;i> 1;
if(arr[center] < temp)
head = center + 1;
else
end = center - 1;
}
//此时head==end,然后后移
int j;
for(j=i-1; j>end; j--){
arr[j+1] = arr[j];
}
//赋值
arr[j+1] = temp;
}
//测试
public static void main(String args[]) {
int arr[] = new int[] { 6, 7, 1, 9, 4, 8, 2, 5, 3 };
binarySort(arr);
System.out.println(Arrays.toString(arr));
}
结果:[1, 2, 3, 4, 5, 6, 7, 8, 9]
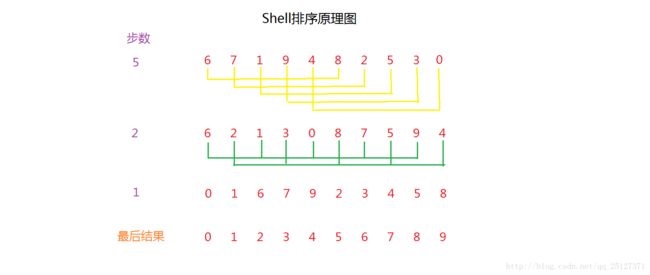
三、希尔排序
1、算法思想:采用的思想是分治法,也叫做缩小增量排序,将整个数组以一个可变的增量为步数分为若干个子数组,然后对各个子数组进行直接插入排序,记为一次循环,然后缩小增量,子数组继续拆分,重复上述操作,直到增量减少为1,即对整个数组进行一次插入排序。
public static void shellSort(int arr[]) {
if (arr == null || arr.length <= 0) {
return;
}
int h = 1;
// 计算出最大增量值
while (h <= arr.length / 3) {
h = h * 3 + 1;
}
while (h > 0) {
// 以h为增量将整个数组分组,将每组的第一个元素视为已排好序,
// 从未排好序的第一个元素开始和前面依次比较
// 第一层循环用于分组
for (int i = h; i < arr.length; i += h) {
// 保存未排序部分的一个元素值
int temp = arr[i];
while (i > 0 && temp < arr[i - h]) {
// 后移
arr[i] = arr[i - h];
i -= h;
}
// 将temp放到空白处
arr[i] = temp;
}
// 计算新的增量
h = (h - 1) / 3;
}
}
//测试
public static void main(String args[]) {
int arr[] = new int[] { 6, 7, 1, 9, 4, 8, 2, 5, 3 };
shellSort(arr);
System.out.println(Arrays.toString(arr));
}
结果:[1, 2, 3, 4, 5, 6, 7, 8, 9]
4、分析
希尔排序时间复杂度根据其增量而定,一般增量都使用h=h*3+1,此时的最优时间复杂度为O(nlog3/2),最坏情况为O(n^2)。空间复杂度为O(1)。因为在排序过程中已经有序的部分排完一次后可能会乱序,所以希尔排序是不稳定排序。