LR(0) 文法分析器
实验介绍
LR(0)分析表是LR(0)分析器的重要组成部分,它是总控程序分析动作的依据。对于不同的文法,LR(0)分析表不同,它可以用一个二维数组表示,行标为状态号,列标为文法符号和’#’号,分析表的内容可由两部分组成,一部分为动作(ACTION)表,它表示当前状态下所面临输入符应做的动作是移进、归约、接受或出错,动作表的行标只包含终结符和’#’,另一部分为转换表(GOTO),它表示在当前状态下面临文法符号时应转向的下一个状态,相当于识别活前缀的有限自动机DFA的状态转换矩阵。因此构造一个文法的LR(0)分析表时,首先应构造识别活前缀的自动机DFA,这样可以很方便地利用DFA的项目集和状态转换函数构造它的LR(0)分析表,在实际应用中为了节省存储空间,通常把关于终结符部分的GOTO表和ACTION表重叠,也就是把当前状态下面临终结符应作的移进-归约动作和转向动作用同一数组元素表示。
实验代码
source.txt 保存了文法
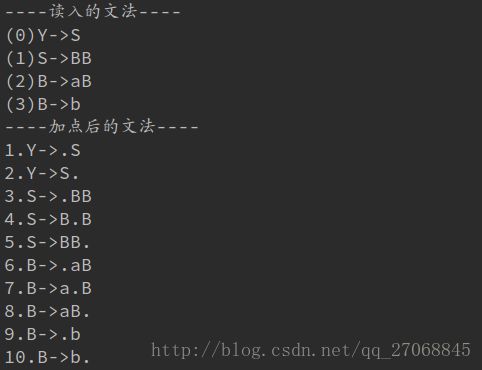
Y->S
S->BB
B->aB
B->bmain.py 保存了程序源码
VN = [] # 非终结符
VT = [] # 终结符
NFA = [] # NFA表
DFA = [] # DFA表
grammar = [] # 读入的文法
doted_grammar = [] # 加点后的文法
VN2Int = {} # 非终结符映射
VT2Int = {} # 终结符映射
action = [] # action表
goto = [] # goto表
DFA_node = [] # DFA节点表
status_stack = [] # 状态栈
symbol_stack = [] # 符号栈
now_state = '' # 栈顶状态
input_ch = '' # 栈顶字符
input_str = '' # 输入串
location = 0 # 输入位置
now_step = 0 # 当前步骤
# 读取文法
def read_grammar(file_name):
global grammar
with open(file_name, 'r') as file:
for line in file:
line = line.replace('\n', "")
grammar.append(line)
file.close()
# 找到终结符和非终结符
def find_term_non():
global grammar
n = int(len(grammar))
temp_vt = []
l = 0
for i in range(n):
X, Y = grammar[i].split('->')
if X not in VN:
VN.append(X)
VN2Int.update({X: l})
l += 1
for Yi in Y:
temp_vt.append(Yi)
m = 0
for i in temp_vt:
if i not in VN and i not in VT:
VT.append(i)
VT2Int.update({i: m})
m += 1
VT.append('#')
VT2Int.update({'#': m})
# 在字符串某个位置加点
def add_char2str(grammar_i, i):
grammar_i = grammar_i[0:i] + '.' + grammar_i[i:len(grammar_i)]
return grammar_i
# 给文法加点
def add_dot():
global doted_grammar
j = 0
n = 0
for i in grammar:
for k in range(len(i) - 2):
doted_grammar.append([])
doted_grammar[n].append(add_char2str(i, k + 3))
doted_grammar[n].append('false')
n += 1
j += 1
# 显示加点后的文法
def print_doted_grammar():
print('----加点后的文法----')
j = 1
for i in doted_grammar:
print('%d.%s' % (j, i[0]))
j += 1
# 显示读入文法
def print_read_grammar():
print('----读入的文法----')
j = 0
for i in grammar:
print('(%d)%s' % (j, i))
j += 1
# 初始化NFA
def init_nfa():
global NFA
for row in range(len(doted_grammar)):
NFA.append([])
for col in range(len(doted_grammar)):
NFA[row].append('')
# 找到点的位置
def find_pos_point(one_grammar):
return one_grammar.find('.')
# 文法是否以start开头,以'.'开始
def is_start(grammar_i, start):
if grammar_i[0].find(start, 0, 1) + grammar_i[0].find('.', 3, 4) == 3:
return True
else:
return False
# 查找以start开头,以'.'开始的文法,返回个数
def find_node(start, grammar_id):
num = 0
for i in doted_grammar:
if is_start(i, start):
grammar_id[num] = doted_grammar.index(i)
num += 1
return num
# 构造NFA
def make_nfa():
global NFA
grammar_id = []
for i in range(10):
grammar_id.append('')
init_nfa()
i = 0
for grammar_i in doted_grammar:
pos_point = find_pos_point(grammar_i[0]) # 找到点的位置
if not pos_point + 1 == len(grammar_i[0]):
NFA[i][i + 1] = grammar_i[0][pos_point + 1]
if grammar_i[0][pos_point + 1] in VN: # 点后面跟着非终结符
j = find_node(grammar_i[0][pos_point + 1], grammar_id)
for k in range(j):
NFA[i][grammar_id[k]] = '*'
add_more(i, grammar_id[k])
i += 1
# 查找关联
def add_more(i, j):
global NFA
grammar_id = []
for k in range(10):
grammar_id.append('')
pos_point = find_pos_point(doted_grammar[j][0])
if not pos_point + 1 == len(doted_grammar[j][0]):
if doted_grammar[j][0][pos_point + 1] in VN:
j = find_node(doted_grammar[j][0][pos_point + 1], grammar_id)
for k in range(j):
NFA[i][grammar_id[k]] = '*'
add_more(i, grammar_id[k])
# 初始化DFA
def init_dfa():
global DFA
for row in range(len(doted_grammar)):
DFA.append([])
for col in range(len(doted_grammar)):
DFA[row].append('')
# 连接
def add_state(to, fro):
for i in range(len(doted_grammar)):
if not NFA[to][i] == '' and not NFA[to][i] == '*':
DFA[to][i] = NFA[to][i]
if not NFA[fro][i] == '' and not NFA[fro][i] == '*': # from可连接的点
DFA[to][i] = NFA[fro][i]
# 构造DFA
def make_dfa():
global NFA, doted_grammar, DFA_node
init_dfa()
for i in range(len(doted_grammar)):
DFA_node.append([])
for j in range(len(doted_grammar)):
DFA_node[i].append("")
for i in range(len(doted_grammar)):
if doted_grammar[i][1] == 'false':
k = 0
DFA_node[i][k] = doted_grammar[i][0]
k += 1
doted_grammar[i][1] = 'true'
for j in range(len(doted_grammar)):
if NFA[i][j] == '*': # 有ε弧
DFA_node[i][k] = doted_grammar[j][0]
k += 1
doted_grammar[j][1] = 'true'
add_state(i, j)
# 初始化LR分析表
def init_lr_table():
global doted_grammar, action, goto
for i in range(len(doted_grammar)):
action.append([])
goto.append([])
for j in range(len(VT)):
action[i].append('')
for j in range(len(VN)):
goto[i].append(-1)
# 有无规约项
def need_protocol(point):
global DFA_node
if not DFA_node[point][0] == "":
for i in range(10):
if DFA_node[point][i].endswith('.'):
return DFA_node[point][i]
else:
return None
else:
return None
# 根据文法内容找到文法编号
def find_grammar(string):
global grammar
tmp = string[0: len(string) - 1]
for i in range(len(grammar)):
if tmp == grammar[i]:
return i
# 填充LR分析表
def fill_lr_table():
global doted_grammar, VT2Int, VN2Int, VN
init_lr_table()
for i in range(len(doted_grammar)):
if need_protocol(i):
num = find_grammar(need_protocol(i))
tmp = 'r' + str(num)
for j in range(len(VT)):
if i == 1:
action[i][VT2Int['#']] = 'acc'
else:
action[i][j] = tmp
else:
for j in range(len(doted_grammar)):
if not DFA[i][j] == '':
if DFA[i][j] in VN:
goto[i][VN2Int.get(DFA[i][j], -1)] = j
else:
tmp = 's' + str(j)
action[i][VT2Int.get(DFA[i][j], -1)] = tmp
# 显示LR分析表
def print_lr_table():
global VT, VN, doted_grammar, action, goto
# 表头
print('----LR分析表----')
print('\t\t|\t', end='')
print(('%3s' % '') * (len(VT) - 2), end='')
print('Action', end='')
print(('%3s' % '') * (len(VT) - 2), end='')
print('\t|\t', end='')
print(('%3s' % '') * (len(VN) - 2), end='')
print('GOTO', end='')
print(('%3s' % '') * (len(VN) - 2), end='')
print('\t|')
print('\t\t\t', end='')
for i in VT:
print('%3s\t' % i, end='')
print('\t|\t', end='')
k = 0
for i in VN:
if not k == 0:
print('%3s\t' % i, end='')
k += 1
print('\t|')
for i in range(len(doted_grammar)):
print('-----', end='')
print()
# 表体
for i in range(len(doted_grammar)):
print('%5d\t|\t' % i, end='')
for j in range(len(VT)):
print('%4s' % action[i][j], end='')
print('\t|\t', end='')
for j in range(len(VN)):
if not j == 0:
if not goto[i][j] == -1:
print('%4s' % goto[i][j], end='')
else:
print('\t', end='')
print('\t|')
for i in range(len(doted_grammar)):
print('-----', end='')
print()
# 判断分析是否完成
def is_end():
if input_str[location:len(input_str)] == '#':
if symbol_stack[-1] == 'X' and symbol_stack[-2] == '#':
return True
else:
return False
else:
return False
# 输出
def output():
global now_step, status_stack, symbol_stack, input_str, now_state
print('%d\t\t' % now_step, end='')
now_step += 1
print('%-20s' % status_stack, end='')
print('%-25s' % symbol_stack, end='')
print('%-22s' % input_str[location:len(input_str)], end='')
# 统计产生式右部的个数
def count_right_num(grammar_i):
return len(grammar_i) - 3
# 规约
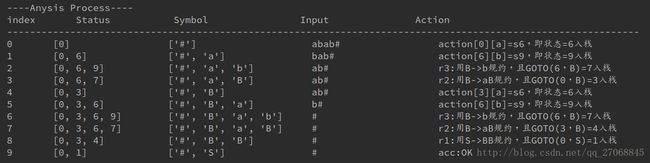
def do_stipulations():
global status_stack, input_str, symbol_stack, location, now_state, input_ch
print('----Anysis Process----')
print("index\t\t", end='')
print('%-17s' % 'Status', end='')
print('%-22s' % 'Symbol', end='')
print('%-20s' % 'Input', end='')
print('Action')
for i in range(len(doted_grammar)):
print('-----------', end='')
print()
symbol_stack.append('#')
status_stack.append(0)
while not is_end():
now_state = status_stack[-1]
input_ch = input_str[location]
output()
find = action[now_state][VT2Int[input_ch]]
if find[0] == 's':
symbol_stack.append(input_ch)
status_stack.append(int(find[1]))
location += 1
print('action[%s][%s]=s%s,即状态=%s入栈' % (now_state, input_ch, find[1], find[1]))
elif find[0] == 'r':
num = int(find[1])
g = grammar[num]
right_num = count_right_num(g)
for i in range(right_num):
status_stack.pop()
symbol_stack.pop()
symbol_stack.append(g[0])
now_state = status_stack[-1]
symbol_ch = symbol_stack[-1]
find = goto[now_state][VN2Int.get(symbol_ch, -1)]
if find == -1:
print('****分析失败****')
break
status_stack.append(find)
print('r%s:用%s规约,且GOTO(%s,%s)=%s入栈' % (num, g, status_stack[-2], symbol_stack[-1], find))
else:
break
print("acc:OK")
if __name__ == '__main__':
# 读入文法,给文法加点
read_grammar('src.txt')
add_dot()
print_read_grammar()
print_doted_grammar()
find_term_non()
# 构造NFA
make_nfa()
# 构造DFA
make_dfa()
# 构造分析表
fill_lr_table()
print_lr_table()
# 规约
input_str = 'abab#'
do_stipulations()