Cantor三分集的递归算法

Cantor三分集的递归算法

---

小前言

今天在unity3d上借用Cantor三分集算法思想实现了如下一个分形效果：

虽然整体看上去不像 三分集的原型：



做完倍感有趣啊哈哈

---

Cantor三分集算法思想介绍

按照Cantor三分集的生成规则，用下图表示空间画线关系。

其中(ax,ay)–(bx,by)为初始线段，(ax,ay)–(cx,cy)和(dx,dy)–(bx,by)为初始线段3等分

后去掉中间线段所剩下的两个线段。以后操作都按照这种简单规则进行递归。

---

1.算法与步骤

• ①如上图，给定初始直线两端点坐标(ax,ay)和(bx,by)，按如下生成规则计算各关键点坐标：
  

  
  

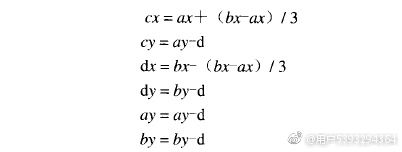
                其中，d为一个常量，代表上下两层线段之间的距离。
  

• ②利用递归算法，将计算出来的新点分别对应于(ax,ay)和(bx,by)，即：
  

  
  
  
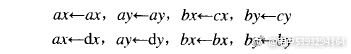
  再利用步骤①中关系计算出下一级新点(cx,cy)和(dx,dy)，并压入堆栈。

• ③给定一个小量c，当(bx,by)

---

2.补充说明

• ①Cantor集被分解到无穷时是一种状态，但无穷只存在于想象之中，计算机无法做到，所以算法中设置了一个小量指标c，用来停止递归。

• ②常量d是为了使Cantor三分集每层结果不重叠，方便看清它的自相似性。

---

3.Java程序例子

• 主要递归方法为：

public void drawShape(Graphics g, double ax, double ay, double bx, double by){
       double c=1;
       if((bx - ax) < c){
         g.drawLine((int) ax, (int) ay, (int) bx, (int) by);
       }else{
          double cx = 0, cy = 0, 
                 dx = 0, dy = 0;
          g.drawLine((int) ax, (int) ay, (int) bx, (int) by);
          cx = ax + (bx - ax) / 3;
          cy = ay +50;
          dx = bx - (bx - ax) / 3;
          dy = by +50;
          ay = ay +50;
          by = by +50;
         drawShape(g,ax, ay, cx, cy);
         drawShape(g,dx, dy, bx, by);

       }        
   }   

---

可在IDE环境中运行该JApplet程序(Cantor.java)：

import java.awt.*;
import javax.swing.*;
import java.lang.*;
public class Cantor extends JApplet{ 
 public void init(){
    new Cantor();
  }
  public void frameSet(){
   Cantor shapes = new Cantor();
   JFrame fra = new JFrame("welcome");
   fra.getContentPane().add(shapes,BorderLayout.CENTER);
         fra.setSize(new Dimension(670,400));
         fra.setResizable(false);
          fra.setVisible(true);

 }
  public static void main(String args[]){
    new Cantor().frameSet();

  }

   public void paint(Graphics g){
       g.setColor(Color.black);
       drawShape(g,100, 100, 800, 100);
   }
   public void drawShape(Graphics g, double ax, double ay, double bx, double by){
       double c=1;
       if((bx - ax) < c){
         g.drawLine((int) ax, (int) ay, (int) bx, (int) by);
       }else{
          double cx = 0, cy = 0, 
                 dx = 0, dy = 0;
          g.drawLine((int) ax, (int) ay, (int) bx, (int) by);
          cx = ax + (bx - ax) / 3;
          cy = ay +50;
          dx = bx - (bx - ax) / 3;
          dy = by +50;
          ay = ay +50;
          by = by +50;
         drawShape(g,ax, ay, cx, cy);
         drawShape(g,dx, dy, bx, by);

       }        
   }   
}

---

这是一只编程小喵，经常出没在喵屋[AudioMiao]中，挖挖[喵的Github]，瞧瞧世界。