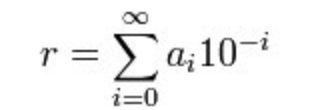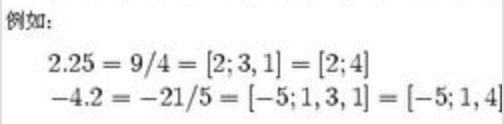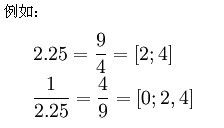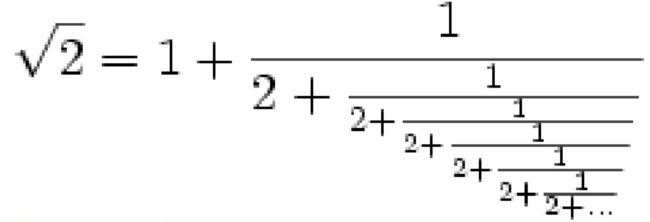连分数
0x01 连分数的定义
连分数(continued fraction)是特殊繁分数。
如果a0,a1,a2,…an,…都是整数,则将分别称为无限连分数和有限连分数。可简记为a0 ,a1,a2,…,an,…和a0,a1,a2,…,an。
一般一个有限连分数表示一个有理数,一个无限连分数表示一个无理数。
如果a0,a1,a2,…,an,…都是实数,可将上述形式连分数分别叫无限连分数和有限连分数 。
近代数学的计算需要,还可将连分数中的a0,a1 ,a2,…,an,…取成以x为变元的多项式。
在近代计算数学中它常与某些微分方程式差分方程有关,与某些递推关系有关的函数构造的应用相联系。
以上内容来自百度百科的词条。
非常拗口还难以理解吧?
0x02 连分数表示法的意义
研究连分数的动机源于想要有实数在“数学上纯粹”的表示。
在十进制表示法系统下,我们都习惯于把实数的小数表示成:
这里的a0 可以是任意整数,其它ai 都是 {0, 1, 2, ..., 9} 的一个元素。
在这种表示中,例如数 π 被表示为整数序列 {3, 1, 4, 1, 5, 9, 2, ...}。
这种小数表示有些问题。
例如,在这种情况下使用常数 10 是因为我们使用了 10进制系统。我们还可以使用 8进制或 2 进制系统。
另一个问题是很多有理数在这个系统内缺乏有限表示。例如,数 1/3 被表示为无限序列 {0, 3, 3, 3, 3, ....}。
连分数表示法是避免了实数表示的这两个问题。
让我们考虑如何描述一个数如 415/93,约为 4.4624。近似为 4,而实际上比 4 多一点,约为 4 + 1/2。但是在分母中的 2 是不准确的;更准确的分母是比 2 多一点,约为 2 + 1/6,所以 415/93 近似为 4 + 1/(2 + 1/6)。但是在分母中的 6 是不准确的;更准确分母是比 6 多一点,实际是 6+1/7。所以 415/93 实际上是 4+1/(2+1/(6+1/7))。这样才准确。
去掉表达式 4 + 1/(2 + 1/(6 + 1/7)) 中的冗余部分可得到简略记号 [4; 2, 6, 7]。
0x03 连分数的分类
有限连分数
所有有限连分数都表示一个有理数,而所有有理数都可以按两种不同的方式表示为有限连分数。
这两种表示除了最终项之外都是一致的。在较长的连分数表示,其最终项是 1;较短的表示去掉了最后的 1,而向新的终项加 1。
无限连分数
所有无限连分数都是无理数,而所有无理数可用一种精确的方式表示为无限连分数。
无理数的无限连分数表示是非常有用的,因为它的初始段提供了对这个数的优异的有理数逼近。
这些有理数可以叫做这个连分数的收敛(convergent,也译为“渐进”)。
所有偶数编号的收敛都小于最初的数,而奇数编号的收敛都大于它。
0x04 连分数的倒数
有理数的连分数表示和它的倒数除了依据这个数小于或大于 1 而分别左移或右移一位以外是相同的。
换句话说:
和
![]()
互为倒数。
这是因为如果 a是整数,接着如果x<1,则x=0+1/(a+1/b)且1/x=a+1/b,而且如果x>1,则x=a+1/b且1/x=0+1/(a+1/b)。
带有最后的数生成对x和它的倒数是同样的连数的余数。
0x05 如何找到一个数的连分数
有理小数表示为连分数
要计算实数r的连分数表示,可先写下r的整数部分,然后从r减去这个整数部分。如果差为 0 则停止;否则找到这个差的倒数并重复。
当且仅当r是有理数适用。
任意分数表示为连分数(辗转相除法)
无理数表示为连分数
0x06 连分数表示法的意义
由此可以看出:
连分数的截断值是从左右两个方向交叉逼近真值的。
每个截断值我们都称之为该分数的收敛子(渐进分数),他们都交替地大于和小于真值。
※以上内容整理自多个来源※
1、百度百科 - 《连分数》
2、百度文库 - PPT《连分数》