手写机器学习算法系列02——梯度下降

引言

在上一篇手写机器学习算法系列01——线性回归中，我们已经成功地通过矩阵求偏导的方法算出目标函数$J(\Theta )=\frac{1}{2m}{\sum }_{i=1}^m(X^{(i)}\Theta -y^{(i)}{)}^2$的极小值点，结论是当$\Theta =(X^{T}X{)}^{-1}{X}^{T}y$时，可以拟合出最符合当前训练集样本的线性方程。

这种最小二乘法的优势在于代码实现会十分简单，直接将样本数据套用以上公式即可求解出任何线性回归模型的参数值。不过缺点也很突出：矩阵乘法、矩阵求逆等操作具有$O(n^3)$的时间复杂度，如果样本和特征值少还好，一旦有成千上万的数据量以及几十上百的特征数，训练样本所消耗的时间几乎是不可忍耐的。另外这个方法只适用于线性模型，不适用于其他模型比如逻辑回归。

因此，我们需要学习另一种普遍性更强的方法来求解目标函数的极值点——梯度下降。

梯度下降法基本思想

通俗地讲，梯度下降法可以类比为下山的过程：

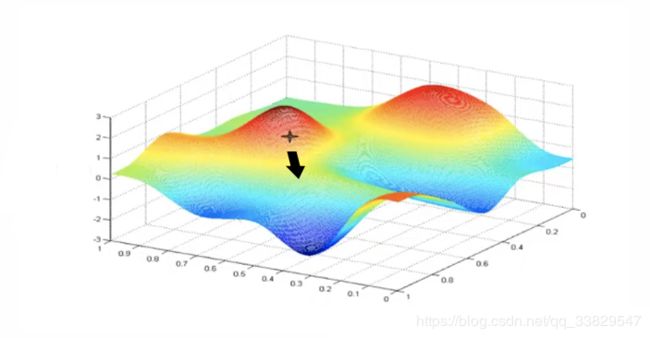
假如一个人在上图的山里，想走到山脉的最低点处，并且山上大雾弥漫，看不清山的全貌也不知道自己具体在山中的哪个位置。不过这个人有特殊的能力，能够测量出自己所在的点坡度最大的方向。于是这个人想出了个办法，先测量下自己现在往哪个方向走坡度最大，往这个方向走一小段距离，再测量当前所在位置往哪个方向走坡度最大，再继续往这个方向走，周而复始下去，最终走到了最低点处。

这个过程用数学公式表述：

$${\theta }_{i+1}={\theta }_i-a\times \nabla J({\theta }_i)$$

• $\nabla J({\theta }_i)$是当前位置的梯度，相当于当前位置最陡的方向
• ${\theta }_i$相当于这个人现在所处的位置
• ${\theta }_{i+1}$相当于下一步将要走到的位置
• $a$叫学习率或者步长，用来控制“下山”时每一步走的距离。

慢着，你是不是觉得这个过程有漏洞？按照这个方法，这个人真的就一定会走到山的最低点处吗？像上图的山脉延绵起伏，会不会走到某一个局部的低洼地带，而这个局部的低洼地带就一定会是整个山脉的最低点吗？就像下图：

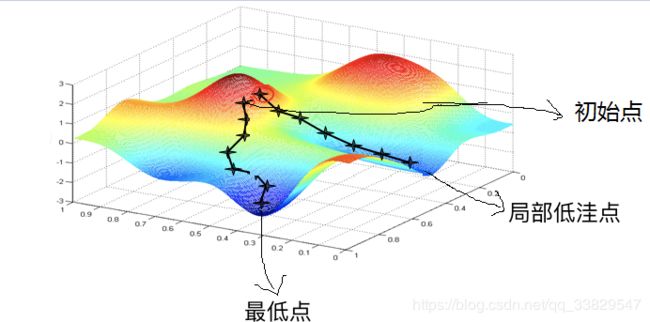
可以看到如果起始点不一样，可能的“下山”路径也会不一样，如果走下面一条路，那么能够成功地走到最低点，可如果走了右边那条路，则会陷入一个局部的低洼点，而不是最低点。
因此起始点的选择是模型训练好坏的重要影响因素，但是初始点的选择又往往是个玄学问题，所以机器学习中常常会有玄学调参的说法。。。

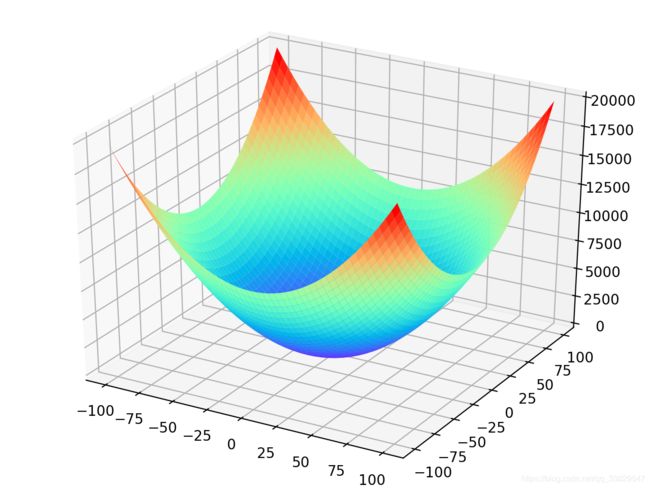
不过这个问题在线性回归中是不存在的，因为线性回归的目标函数是一个凸函数，比如二元线性函数的目标函数长的类似于碗状：

容易看出，只会有一个局部极小值点，也就是最低点。

了解了梯度下降法的基本思想和公式，我们来找几个函数，手动展现梯度下降过程，验证方法的可行性。

一元函数梯度下降案例

先来个简单的函数：

$$J(\theta )={\theta }^2$$

这个函数肯定都认识，我们在脑海进行函数图像的想象也能知道最低点在$\theta =0$处。现在我们用梯度下降的公式来算出最低点。公式我就贴心地搬下来了：

$${\theta }_{i+1}={\theta }_i-a\times \nabla J({\theta }_i)$$

咱们先算出$\nabla J({\theta }_i)$：

$$\nabla J({\theta }_i)=2{\theta }_i$$

再随便选一个初始点${\theta }_0$，比如：

$${\theta }_0=-1$$

这里初始点能够随便选是因为$J(\theta )={\theta }^2$是凸函数，只有一个极小值点。

再设定一个学习率(步长)：

$$a=0.4$$

接下来进行梯度下降的过程:

$$\begin{array}{rl}{\theta }_0& =-1\\ & \\ {\theta }_1& ={\theta }_0-a\times \nabla J({\theta }_0)\\ & =-1-0.4\times 2\times (-1)\\ & =-0.2\\ & \\ {\theta }_2& ={\theta }_1-a\times \nabla J(\theta 1)\\ & =-0.04\\ & \\ {\theta }_3& ={\theta }_2-a\times \nabla J(\theta 2)\\ & =-0.008\\ & \\ {\theta }_4& ={\theta }_3-a\times \nabla J(\theta 3)\\ & =-0.0016\\ & \end{array}$$

可以看到$\theta$的取值越来越趋近于最低点$0$，如果愿意我们可以一直算下去，然而达到一定的精度后我们就可以认为模型已经训练完成了。

以上过程可以用下图来表示：

二元函数梯度下降案例

多元函数的梯度实际上是一个向量，当然刚才的一元函数的梯度也可以看做是向量，只不过只有左右两个方向。

$$J(x,y)=x^2+y^2$$

对$J(x,y)$求梯度其实就是分别求$x$与$y$的偏导：

$$\begin{array}{rl}\nabla J(x,y)& =<\frac{\partial J(x,y)}{\partial x},\frac{\partial J(x,y)}{\partial y}>\\ & =<2x,2y>\end{array}$$

同样，我们先假设起始点的位置：

$$(x_0,y_0)=(1,3)$$

学习率(步长)我们设定为：

$$a=0.1$$

接着我们手算梯度下降：

$$\begin{array}{rl}(x_0,y_0)& =(1,3)\\ & \\ (x_1,y_1)& =(x_0,y_0)-a\times \nabla J(x_0,y_0)\\ & =(1,3)-0.1\times (2,6)\\ & =(0.8,2.4)\\ & \\ (x_2,y_2)& =(x_1,y_1)-a\times \nabla J(x_1,y_1)\\ & =(0.8,2.4)-0.1\times (1.6,4.8)\\ & =(0.64,1.92)\\ & \\ ....& \\ ....& \\ (x_{100},y_{100})& =(1.6296287810675902e^{-10},4.888886343202771e^{-10})\end{array}$$

手写梯度下降算法

前面我们用一元和二元函数实例展示了梯度下降的过程，现在我们来讨论线性回归如何运用梯度下降，并且完成代码的实现。

$$J(\Theta )=\frac{1}{2m}\sum _{i=1}^m(X^{(i)}\Theta -y^{(i)}{)}^2$$

细心的读者会发现这个函数和之前的损失函数相比，前面的$\frac{1}{2}$变成了$\frac{1}{2m}$。

我们知道引入$\frac{1}{2}$的作用是为了方便在求导中约掉后面的平方，并不会影响最终结果。这里又引入了$m$，即除以整体样本的个数。

这么做的目的我们可以想想，如果不除以整体样本的数量，那么针对同一套算法，样本数量越多时，损失值会越大；而样本小的损失值就小。这显然是不科学的，所以需要除以个总体样本数量$m$。

我们为了方便对$J(\Theta )$进行求导，先将$J(\Theta )$展开：

$$\begin{array}{rl}J(\Theta )& =\frac{1}{2m}(X\Theta -y{)}^2\\ & =\frac{1}{2m}(X\Theta -y{)}^T(X\Theta -y)\\ & =\frac{1}{2m}({\Theta }^T{X}^{T}X\Theta -y^{T}X\Theta -{\Theta }^T{X}^{T}y+y^{T}y)\end{array}$$

然后对$J(\Theta )$求导：

$$\begin{array}{rl}\nabla J(\Theta )& =\nabla (\frac{1}{2m}({\Theta }^T{X}^{T}X\Theta -y^{T}X\Theta -{\Theta }^T{X}^{T}y+y^{T}y))\\ & =\frac{1}{2m}(2X^{T}X\Theta -X^{T}y-X^{T}y+0)\\ & =\frac{1}{m}(X^{T}X\Theta -X^{T}y)\\ & =\frac{1}{m}{X}^T(X\Theta -y)\end{array}$$

于是我们可以写出求当前梯度的函数代码实现：

def gradient_function(thetas, X, y):
    '''计算梯度
    '''
    gradient= (1/X.shape[0])np.dot(X.T, np.dot(X, thetas)-y)
    print(gradient)
    return gradient

再根据${\theta }_{i+1}={\theta }_i-a\times \nabla J({\theta }_i)$写出以下循环迭代求梯度并“下山”的函数，循环终止条件为当前位置梯度梯度小于某个很小的值时，这里选用了$1e^{-5}$。

def gradient_descent(X, y, alpha):
    '''梯度下降迭代计算
    '''
    thetas = np.zeros(X.shape[1]).reshape(X.shape[1], 1)
    gradient = gradient_function(thetas, X, y)
    while not np.all(np.absolute(gradient) < 1e-5):
        thetas = thetas-alpha*gradient
        gradient = gradient_function(thetas, X, y)
    return thetas

具体的训练集可以去上一篇博客手写机器学习算法系列01——线性回归中寻找，使用梯度下降训练线性回归模型的完整代码如下：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

def model(thetas, X):
    '''线性模型
    '''
    result = []
    for x in X:
        result.append(np.dot(thetas.reshape(len(thetas)), x))
    return result



def gradient_function(thetas, X, y):
    '''计算梯度
    '''
    gradient= (1/X.shape[0])*np.dot(X.T, np.dot(X, thetas)-y)
    print(gradient)
    return gradient

def gradient_descent(X, y, alpha):
    '''梯度下降迭代计算
    '''
    thetas = np.zeros(X.shape[1]).reshape(X.shape[1], 1)
    gradient = gradient_function(thetas, X, y)
    while not np.all(np.absolute(gradient) < 1):
        thetas = thetas-alpha*gradient
        gradient = gradient_function(thetas, X, y)
    return thetas

if __name__ == "__main__":
    pdData = pd.read_csv("Salary_Data.csv", sep=",", header=None)
    pdData.insert(0, "x0", 1)
    orig_data = pdData.values
    cols = orig_data.shape[1]
    # 拿到特征值(包含x0)
    X = orig_data[:, 0:cols-1]
    # 拿到特征值(不包含x0)
    x = orig_data[:, 1:cols-1]
    # 拿到实际值
    y = orig_data[:, cols-1:cols]
    # 求解θ
    thetas = gradient_descent(X, y,0.01)
    print(thetas)
    # 求解预测值
    y_predict = model(thetas, X)

    plt.figure(figsize=(10, 5))
    # 画出实际值的散点图
    plt.scatter(pdData.iloc[:, 1], pdData.iloc[:, 2])
    plt.xlabel("Working age (Years)")
    plt.ylabel("Salary (RMB)")
    # 画出线性回归方程的图像
    plt.plot(x, y_predict)
    plt.show()