人脸识别的损失函数解读
最近在研究自编码器提取特征做分类和生成、重建。所以细致了解人脸识别的各种损失函数!
文章目录
- 1、概要
- 2、Softmax Loss
- 3、Center Loss
- 4、A-Softmax Loss
- 5、L-Softmax Loss
- 6、CosFace Loss
- 7、AM-Softmax
- 8、ArcFace/Insight Face
- 9、小结一下
- 10、参考链接
1、概要
人脸识别:输入一张图片,进行人脸检测,再提取关键点进行人脸对齐矫正,最后提取人脸特征,进行判别这个人是谁。判别这个人是谁,本质上是分类问题。
既然牵涉到分类,分类的目的就是不同类的类间间距够大,同一类的类内距离足够小。那么我们一步一步介绍人脸识别中常用的损失函数。
2、Softmax Loss
S o f t m a x Softmax Softmax :将特征图扁平化后的输出映射到(0,1)之间,给出每个类的概率。假设最后一层特征图尺度是: 5 ∗ 5 ∗ 1000 5*5*1000 5∗5∗1000 。再将这些特征输入给扁平化 为 [ N N N X 1 1 1] 个向量(这里的 N N N 是 5 ∗ 5 ∗ 1000 = 25000 5*5*1000=25000 5∗5∗1000=25000)。下面扁平化的 [ N N N X 1 1 1] 的向量进入全连接层,全连接层的参数权重是 W W W[ T T T X N N N](这里的 T T T 表示分类的类别数),经过全连接层处理就会得到一个 [ T T T x 1 1 1] 的向量,但是这个向量里面都每个数值的大小都没有限制,或许是无穷大,也有可能是无穷小,均有可能。因此多分类时候,往往在全连接层后面接个 S o f t m a x Softmax Softmax 层。这个层的输入是 [ T T T x 1 1 1] 的向量,输出也是 [ T T T x 1 1 1] 的向量。但是输出的每个向量都归一化到 [ 0 , 1 ] [0,1] [0,1] 之间。这里的 S o f t m a x Softmax Softmax 输出的向量是该样本属于每一类的概率。
S o f t m a x Softmax Softmax公式:
P j = e a j ∑ k = 1 T e a k P_j=\frac{e^{a_j}}{\sum_{k=1}^{T}{e}^{a_k}} Pj=∑k=1Teakeaj
上面公式中的 a j a_j aj 表示这 [ T T T x 1 1 1] 个向量中的第 j j j 个值,而下面分母表示所有值的求和。上式成功的把 P j P_j Pj 归一化到 ( 0 , 1 ) (0,1) (0,1) 之间。优化目标:属于正确标签的预测概率最高。
下面介绍 S o f t m a x L o s s Softmax \ Loss Softmax Loss:
L = − ∑ j = 1 T y i log p j L=-\sum_{j=1}^{T}{y_i} \ {\log{p_j}} L=−j=1∑Tyi logpj上式中的 p j p_j pj 表示 S o f t m a x Softmax Softmax 层输出的第 j j j 的概率值。 y y y 表示一个 [ 1 1 1 x T T T] 的向量,里面的 T T T 列中只有一个为1,其余为0(真实标签的那个为1,其余不是正确的为0)。这个公式有一个更简单的形式是:
L = − log p j L=-\log p_j L=−logpj其中的 j j j 是指当前样本的真实标签。 l o g log log函数是个递增的函数,你预测错的概率会比你预测对的概率要大,因为前面加了一个负号。
图像分类里面常用 S o f t m a x L o s s Softmax \ Loss Softmax Loss。
3、Center Loss
C e n t e r L o s s Center \ Loss Center Loss来自 E C C V 2016 ECCV2016 ECCV2016一篇论文: A D i s c r i m i n a t i v e F e a t u r e L e a r n i n g A p p r o a c h f o r D e e p F a c e R e c o g n i t i o n A \ Discriminative \ Feature \ Learning \ Approach \ for \ Deep \ Face \ Recognition A Discriminative Feature Learning Approach for Deep Face Recognition
对 M N I S T MNIST MNIST数据集进行分类,若损失函数采用上述介绍的 S o f t m a x L o s s Softmax \ Loss Softmax Loss(因为 S o f t m a x L o s s Softmax \ Loss Softmax Loss能够使特征可分),那么最后每个类别数字学出来的特征分布下图,我们可以看出类间距离还是比较小,类内距离比较大的,虽然效果很好:
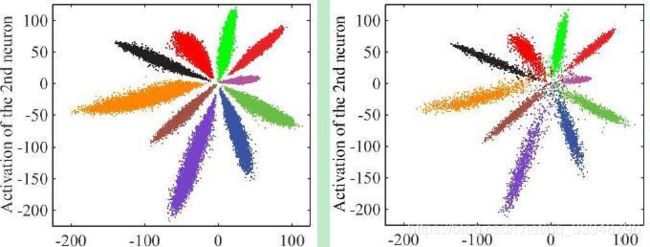
如果损失函数采用 C e n t e r L o s s Center \ Loss Center Loss,那么特征分布如下图,我们可以看出相比于 S o f t m a x L o s s Softmax \ Loss Softmax Loss类间距离变大了,类内距离变小了:

所以我们可以看出 C e n t e r L o s s Center \ Loss Center Loss能够最小化类内距离的同时保证特征可分,来提高特征之间的可判别性!简单地说,给每一类( l a b e l label label)定义一个类中心( C e n t e r Center Center),同一类的数据向类中心靠近,离得远要惩罚!于是 C e n t e r L o s s Center \ Loss Center Loss就出现了。
C e n t e r L o s s = 1 2 m ∑ i = 1 m ∣ x i − c y i ∣ 2 2 Center \ Loss = \frac{1}{2m}\sum_{i=1}^{m}{|x_i-c_{y_i}|_2^{2}} Center Loss=2m1i=1∑m∣xi−cyi∣22其中 c y i c_{y_i} cyi 表示这个样本所对应的第 y i y_i yi 类别的特征中心, m m m 表示每一个 b a t c h batch batch 大小。上述公式的意义是:希望 b a t c h batch batch 中的每个样本特征距离特征中心的距离的平方和越小越好,也就是负责类内差距。
那么上述的 c y i c_{y_i} cyi 每一 b a t c h batch batch 怎么确定的呢?理想情况下, c y i c_{y_i} cyi 需要随着学习到的 f e a t u r e feature feature 进行实时更新,也就是在每一次迭代的时候用整个数据集的 f e a t u r e feature feature 来计算每个类的中心。但是这样时间复杂度高,于是:用 b a t c h batch batch 来更新 c e n t e r center center,每一轮计算一下当前 b a t c h batch batch 数据与 c e n t e r center center 的距离,然后这个距离以梯度的形式叠加到 c e n t e r center center 上。
我们下面对 x i x_i xi 求导: ∂ L c ∂ x i = 1 m ∑ i = 1 m ( x i − c y i ) \frac{\partial L_{c}}{\partial x_i}=\frac{1}{m}\sum_{i=1}^{m}{(x_i - c_{y_i})} ∂xi∂Lc=m1i=1∑m(xi−cyi)这里因为每个 b a t c h batch batch 的数量 m m m 太小,那么每次更新 c e n t e r center center 可能会引起 c e n t e r center center 抖动。那么梯度上面加个限制 α \alpha α,这个值在 0 − 1 0-1 0−1 之间:
Δ c = α m ∑ i = 0 m ( x i − y i ) \Delta c=\frac{\alpha}{m}{\sum_{i=0}^m{}(x_i-y_{i})} Δc=mαi=0∑m(xi−yi)为了最小化类内,最大化类间,即满足特征可分和特征可判别,论文中将 S o f t m a x L o s s Softmax \ Loss Softmax Loss 和 C e n t e r L o s s Center \ Loss Center Loss 结合。

有大牛在 C i f a r 10 Cifar10 Cifar10 和 C i f a r 100 Cifar100 Cifar100 上测试过 C e n t e r L o s s Center \ Loss Center Loss,发现效果并不是很好,准确率明显低于单独的 S o f t m a x Softmax Softmax;在 M N I S T MNIST MNIST上测试加上 C e n t e r L o s s Center \ Loss Center Loss 的 S o f t m a x Softmax Softmax 好于单独的 S o f t m a x Softmax Softmax;所以理解之所以 C e n t e r L o s s Center \ Loss Center Loss 是针对人脸识别的 L o s s Loss Loss是有原因的,因为人脸的中心性更强一些,即一个人的所有脸取平均值之后的人脸我们还是可以辨识是不是这个人,所以 C e n t e r L o s s Center \ Loss Center Loss才能发挥作用。
4、A-Softmax Loss
A − S o f t m a x A-Softmax A−Softmax 来自于 C V P R 2017 CVPR2017 CVPR2017。论文题目:
《 S p h e r e F a c e : D e e p H y p e r s p h e r e E m b e d d i n g f o r F a c e R e c o g n i t i o n 》 《SphereFace: Deep \ Hypersphere \ Embedding \ for \ Face \ Recognition》 《SphereFace:Deep Hypersphere Embedding for Face Recognition》
拿图像分类来说。卷积神经网络提取特征,然后全连接层进行扁平化,再送入 S o f t m a x Softmax Softmax 层实现分类。传统的 S o f t m a x Softmax Softmax 很容易优化,因为它没有尽可能的扩大类间距离,缩小类内距离。
假设最后一层的输出特征向量为 x i x_i xi,它对应的标签是 y i y_i yi ,那么 S o f t m a x Softmax Softmax 又可以写成:
L 总 = 1 N ∑ i L i L_{总}=\frac{1}{N}\sum_{i}L_{i} L总=N1i∑Li其中 L i = − log p j L_{i}=-\log p_j Li=−logpj, p j = e a j ∑ k = 1 T e a k = e f y i ∑ j e f j p_{j}=\frac{e^{a_j}}{\sum_{k=1}^{T}{e}^{a_k}}=\frac{e^{f_{y_i}}}{\sum_j{e^{f_j}}} pj=∑k=1Teakeaj=∑jefjefyi
那么上式 L 总 L_{总} L总可以表示为:
L 总 = 1 N ∑ i L i = 1 N ∑ i − log ( e f y i ∑ j e f j ) L_{总}=\frac{1}{N}\sum_{i}L_{i}=\frac{1}{N}\sum_{i}-\log(\frac{e^{f_{y_i}}}{\sum_je^{f_j}}) L总=N1i∑Li=N1i∑−log(∑jefjefyi)其中 f y i f_{y_i} fyi可以用欧式空间的向量积来表示:
f y i = W y i ∗ x i ( 卷 积 ) = ∣ ∣ W y i ∣ ∣ ∗ ∣ ∣ x i ∣ ∣ ∗ c o s ( θ y i ) ( 乘 积 ) f_{y_i}=W_{y_i}*x_i(卷积)=||W_{y_i}||*||x_i||*cos(\theta_{y_i})(乘积) fyi=Wyi∗xi(卷积)=∣∣Wyi∣∣∗∣∣xi∣∣∗cos(θyi)(乘积)上式中 j j j表示类别总数,上述公式再进一步限制, ∣ ∣ W y i ∣ ∣ = 1 ||W_{y_{i}}||=1 ∣∣Wyi∣∣=1,偏置 b y i = 0 b_{y_i}=0 byi=0(这是一个很重的点哦)。
那么上式又变为:
L 总 = 1 N ∑ i L i L_{总}=\frac{1}{N}\sum_{i}L_{i} L总=N1i∑Li = 1 N ∑ i − log ( e W y i ∗ X i ( 卷 积 ) ∑ j e W j ∗ X i ( 卷 积 ) ) =\frac{1}{N}\sum_{i}-\log(\frac{e^{W_{y_i}*{X_i}(卷积)}}{\sum_je^{W_{j}*X_i(卷积)}}) =N1i∑−log(∑jeWj∗Xi(卷积)eWyi∗Xi(卷积)) = 1 N ∑ i − log ( e ∣ ∣ W y i ∣ ∣ ∗ ∣ ∣ x i ∣ ∣ ∗ c o s ( θ y i ) ( 乘 积 ) ∑ j e ∣ ∣ W j ∣ ∣ ∗ ∣ ∣ x i ∣ ∣ ∗ c o s ( θ j ) ( 乘 积 ) ) =\frac{1}{N}\sum_{i}-\log(\frac{e^{||W_{y_i}||*||x_i||*cos(\theta_{y_i})(乘积)}}{\sum_je^{||W_{j}||*||x_i||*cos(\theta_{j})(乘积)}}) =N1i∑−log(∑je∣∣Wj∣∣∗∣∣xi∣∣∗cos(θj)(乘积)e∣∣Wyi∣∣∗∣∣xi∣∣∗cos(θyi)(乘积)) = 1 N ∑ i − log ( e ∣ ∣ x i ∣ ∣ ∗ c o s ( θ y i ) ( 乘 积 ) ∑ j e ∣ ∣ x i ∣ ∣ ∗ c o s ( θ j ) ( 乘 积 ) ) =\frac{1}{N}\sum_{i}-\log(\frac{e^{||x_i||*cos(\theta_{y_i})(乘积)}}{\sum_je^{||x_i||*cos(\theta_{j})(乘积)}}) =N1i∑−log(∑je∣∣xi∣∣∗cos(θj)(乘积)e∣∣xi∣∣∗cos(θyi)(乘积))上述公式更直白的解释为:二分类, p 1 p_1 p1、 p 2 p_2 p2进行分类,决策界面是 p 1 = p 2 p_1=p_2 p1=p2,上面 ∣ ∣ W ∣ ∣ ||W|| ∣∣W∣∣ 归一化,且偏置 b b b 为 0,那么上述就为:
( W 1 − W 2 ) ∗ x + b 1 − b 2 = c o s ( θ 1 ) − c o s ( θ 2 ) = 0 (W_1-W_2)*x+b_1-b_2=cos(\theta_1)-cos(\theta_2)=0 (W1−W2)∗x+b1−b2=cos(θ1)−cos(θ2)=0那么我们可以得出:一个输入特征 x i x_i xi 属于 y i y_i yi 类,那么该 θ y i \theta y_i θyi的角度应该比所有的其他的类都要小(因为 c o s ( θ ) cos(\theta) cos(θ) 是减函数)。
原始的 S o f t m a x Softmax Softmax,其中的 x x x是类别中学习的特征, θ \theta θ表示 x x x到 W i W_i Wi的角度。小结一下:原始 S o f t m a x Softmax Softmax的目的使得 W 1 ∗ x > W 2 ∗ x W_1*x>W_2*x W1∗x>W2∗x,即 ∥ W 1 ∥ ∗ ∥ x ∥ ∗ c o s ( θ 1 ) > ∥ W 2 ∥ ∗ ∥ x ∥ ∗ c o s ( θ 2 ) ∥W1∥*∥x∥*cos(θ1)>∥W2∥*∥x∥*cos(θ2) ∥W1∥∗∥x∥∗cos(θ1)>∥W2∥∗∥x∥∗cos(θ2),从而得到 x x x 正确的分类结果。如果我们使用 c o s ( m θ 1 ) > c o s ( θ 2 ) cos(m\theta_1)>cos(\theta_2) cos(mθ1)>cos(θ2) 时,才判为类别1,这样我们可以看出决策函数更严格,因为这边的 θ 1 < θ 2 m \theta_1<\frac{\theta_2}{m} θ1<mθ2才会判定类别1;同理, c o s ( θ 1 ) < c o s ( m θ 2 ) cos(\theta_1)<cos(m\theta_2) cos(θ1)<cos(mθ2) 判断为类别2,也就是 θ 2 < θ 1 m \theta_2<\frac{\theta_1}{m} θ2<mθ1,判断为类别2。很抽象,我一开始看的时候也很抽象,所以我们来个直观的解释,超球体解释:
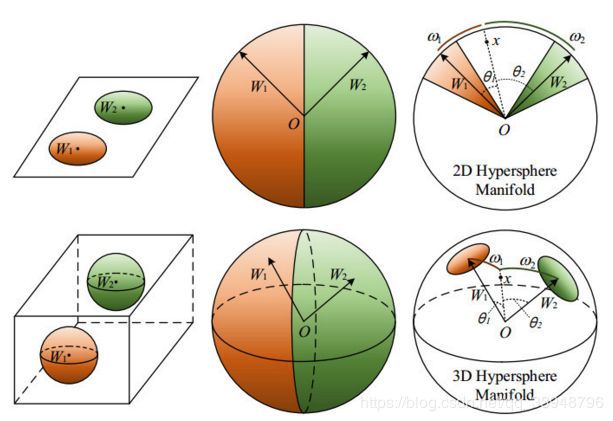 上面的是二维平面,下面是三维超球体解释图。
上面的是二维平面,下面是三维超球体解释图。
A − S o f t m a x A-Softmax A−Softmax使 ∣ ∣ W i ∣ ∣ = 0 , b i a s i = 0 ||W_i||=0,{bias}_i=0 ∣∣Wi∣∣=0,biasi=0,所以依靠的是样本 x x x到 W W W的角度,这个角度越小就越有可能是这一类,而添加一个 m m m的目的:使类间的距离足够大,使类内距离足够小。也就是放大了类间的距离,也因放大了不同类之间的间隔而使类内更聚拢。
但是,原来的 S o f t m a x Softmax Softmax里面的 θ i , j ∈ ( 0 , π ) \theta_{i,j}\in (0,\pi) θi,j∈(0,π) ,如今 m θ i , j ∈ ( 0 , m π ) m\theta_{i,j}\in (0,m\pi) mθi,j∈(0,mπ) 超出了向量之间的夹角函数 c o s cos cos 定义域范围 ( 0 , π ) (0,\pi) (0,π) 咋办?把 n n n个 c o s cos cos堆叠起来变成一个递减的连续的函数,详细见论文!
5、L-Softmax Loss
L − S o f t m a x L-Softmax L−Softmax 来自于 I C M L 2016 ICML2016 ICML2016 的一篇论文:
< L a r g e − M a r g i n S o f t m a x L o s s f o r C o n v o l u t i o n a l N e u r a l N e t w o r k s > <Large-Margin \ Softmax \ Loss \ for \ Convolutional \ Neural \ Networks > <Large−Margin Softmax Loss for Convolutional Neural Networks>
L − S o f t m a x L-Softmax L−Softmax与 A − S o f t m a x A-Softmax A−Softmax的区别在于 ∣ ∣ W i ∣ ∣ ||W_i|| ∣∣Wi∣∣ 没有归一化,偏置不必归0。 L − S o f t m a x L-Softmax L−Softmax与 A − S o f t m a x A-Softmax A−Softmax的过程类似,我简单再介绍一下:
L 总 = 1 N ∑ i L i L_{总}=\frac{1}{N}\sum_{i}L_{i} L总=N1i∑Li = 1 N ∑ i − log ( e W y i ∗ X i ( 卷 积 ) ∑ j e W j ∗ X i ( 卷 积 ) ) =\frac{1}{N}\sum_{i}-\log(\frac{e^{W_{y_i}*{X_i}(卷积)}}{\sum_je^{W_{j}*X_i(卷积)}}) =N1i∑−log(∑jeWj∗Xi(卷积)eWyi∗Xi(卷积)) = 1 N ∑ i − log ( e ∣ ∣ W y i ∣ ∣ ∗ ∣ ∣ x i ∣ ∣ ∗ c o s ( θ y i ) ( 乘 积 ) ∑ j e ∣ ∣ W j ∣ ∣ ∗ ∣ ∣ x i ∣ ∣ ∗ c o s ( θ j ) ( 乘 积 ) ) =\frac{1}{N}\sum_{i}-\log(\frac{e^{||W_{y_i}||*||x_i||*cos(\theta_{y_i})(乘积)}}{\sum_je^{||W_{j}||*||x_i||*cos(\theta_{j})(乘积)}}) =N1i∑−log(∑je∣∣Wj∣∣∗∣∣xi∣∣∗cos(θj)(乘积)e∣∣Wyi∣∣∗∣∣xi∣∣∗cos(θyi)(乘积)) = 1 N ∑ i − log ( e ∣ ∣ x i ∣ ∣ ∗ c o s ( θ y i ) ( 乘 积 ) ∑ j e ∣ ∣ x i ∣ ∣ ∗ c o s ( θ j ) ( 乘 积 ) ) =\frac{1}{N}\sum_{i}-\log(\frac{e^{||x_i||*cos(\theta_{y_i})(乘积)}}{\sum_je^{||x_i||*cos(\theta_{j})(乘积)}}) =N1i∑−log(∑je∣∣xi∣∣∗cos(θj)(乘积)e∣∣xi∣∣∗cos(θyi)(乘积))上述公式更直白的解释为:二分类, x x x属于类别1,我们就希望 W 1 ∗ x > W 2 ∗ x W_1*x>W_2*x W1∗x>W2∗x。我们把它转成点积,得:
∣ ∣ W 1 ∣ ∣ ∗ ∣ ∣ x ∣ ∣ ∗ c o s ( θ 1 ) > ∣ ∣ W 2 ∣ ∣ ∗ ∣ ∣ x ∣ ∣ ∗ c o s ( θ 2 ) ||W_1||*||x||*cos(\theta_1)>||W_2||*||x||*cos(\theta_2) ∣∣W1∣∣∗∣∣x∣∣∗cos(θ1)>∣∣W2∣∣∗∣∣x∣∣∗cos(θ2)那么 L − S o f t m a x L-Softmax L−Softmax 将上面表达式修改为:
∣ ∣ W 1 ∣ ∣ ∗ ∣ ∣ x ∣ ∣ ∗ c o s ( m θ 1 ) > ∣ ∣ W 2 ∣ ∣ ∗ ∣ ∣ x ∣ ∣ ∗ c o s ( θ 2 ) ||W_1||*||x||*cos(m\theta_1)>||W_2||*||x||*cos(\theta_2) ∣∣W1∣∣∗∣∣x∣∣∗cos(mθ1)>∣∣W2∣∣∗∣∣x∣∣∗cos(θ2)其中 0 < θ 1 < π m 0<\theta_1<\frac{\pi}{m} 0<θ1<mπ。 m m m值越大则学习的难度也越大。因此通过这种方式定义损失会逼得模型学到类间距离更大的,类内距离更小的特征。

6、CosFace Loss
来自于 2018 2018 2018论文:
< C o s F a c e : L a r g e M a r g i n C o s i n e L o s s f o r D e e p F a c e R e c o g n i t i o n > <CosFace: Large \ Margin \ Cosine \ Loss \ for \ Deep \ Face \ Recognition> <CosFace:Large Margin Cosine Loss for Deep Face Recognition>
L M C L LMCL LMCL从余弦的角度思考 S o f t m a x L o s s Softmax \ Loss Softmax Loss:
L 总 = 1 N ∑ i L i = 1 N ∑ i − log ( p i ) = 1 N ∑ i − log ( e f y i ∑ j e f j ) L_{总}=\frac{1}{N}\sum_{i}L_{i}=\frac{1}{N}\sum_{i}-\log(p_i)=\frac{1}{N}\sum_{i}-\log(\frac{e^{f_{y_i}}}{\sum_je^{f_j}}) L总=N1i∑Li=N1i∑−log(pi)=N1i∑−log(∑jefjefyi)其中 f j = W j ∗ x = ∣ ∣ W j ∣ ∣ ∗ ∣ ∣ x ∣ ∣ ∗ c o s ( θ j ) f_j=W_j*x=||W_j||*||x||*cos(\theta_j) fj=Wj∗x=∣∣Wj∣∣∗∣∣x∣∣∗cos(θj),其中余弦代表特征向量与权重向量的角度余弦值。
人脸识别是根据两个特征向量之间的余弦相似度计算的。这表明,特征向量 x x x的范数是对评分功能没有贡献,于是,通过 L 2 L2 L2归一化范式将 ∣ ∣ W j ∣ ∣ ||W_j|| ∣∣Wj∣∣设定为1,将 ∣ ∣ x j ∣ ∣ ||x_j|| ∣∣xj∣∣设定为 s s s,于是 L o s s Loss Loss公式变成了如下:
L 总 = 1 N ∑ i L i = 1 N ∑ i − log ( e s ∗ c o s ( θ y i , i ) ∑ j e s ∗ c o s ( θ j , i ) ) L_{总}=\frac{1}{N}\sum_{i}L_{i}=\frac{1}{N}\sum_{i}-\log(\frac{e^{{s*cos(\theta_{y_i},i)}}}{\sum_je^{s*cos(\theta_{j},i)}}) L总=N1i∑Li=N1i∑−log(∑jes∗cos(θj,i)es∗cos(θyi,i))
接下来,作者把余弦边缘项 m m m加上去,与 A − S o f t m a x A-Softmax A−Softmax不同的是:此时的 m m m不是乘积项,而是减法。
L 总 = 1 N ∑ i L i = 1 N ∑ i − log ( e s ∗ ( c o s ( θ y i , i ) − m ) e s ∗ ( c o s ( θ j , i ) − m ) + ∑ j ≠ y i e s ∗ ( c o s ( θ j , i ) − m ) ) L_{总}=\frac{1}{N}\sum_{i}L_{i}=\frac{1}{N}\sum_{i}-\log(\frac{e^{{s*(cos(\theta_{y_i},i)-m)}}}{{e^{s*(cos(\theta_{j},i)-m)}}+{\sum_{j\neq y_i}e^{s*(cos(\theta_{j},i)-m)}}}) L总=N1i∑Li=N1i∑−log(es∗(cos(θj,i)−m)+∑j̸=yies∗(cos(θj,i)−m)es∗(cos(θyi,i)−m))同时满足: W = W ∣ ∣ W ∣ ∣ W=\frac{W}{||W||} W=∣∣W∣∣W s = x = x ∣ ∣ x ∣ ∣ s=x=\frac{x}{||x||} s=x=∣∣x∣∣x W j ∗ x i = 1 ∗ 1 ∗ c o s ( θ j , i ) = c o s ( θ j , i ) W_j*x_i=1*1*cos(\theta_j,i)=cos(\theta_j,i) Wj∗xi=1∗1∗cos(θj,i)=cos(θj,i)所以,其特征会分布在一个超球面上。下图为二维和高维示意图:

7、AM-Softmax
这一部分主要参考下面链接,大牛写的特棒!https://blog.csdn.net/fire_light_/article/details/79602310。
该损失函数来自于 2018 2018 2018论文:
< A d d i t i v e M a r g i n S o f t m a x f o r F a c e V e r i f i c a t i o n > <Additive \ Margin \ Softmax \ for \ Face \ Verification> <Additive Margin Softmax for Face Verification>。个人感觉 A M − S o f t m a x AM-Softmax AM−Softmax 与 C o s − F a c e Cos-Face Cos−Face 撞车了,不管啦,那就解读一下上个没解释的一些问题。
首先再回顾一下 S o f t m a x Softmax Softmax 和 A − S o f t m a x A-Softmax A−Softmax:
L 总 = 1 N ∑ i L i L_{总}=\frac{1}{N}\sum_{i}L_{i} L总=N1i∑Li = 1 N ∑ i − log ( e W y i ∗ X i ( 卷 积 ) ∑ j e W j ∗ X i ( 卷 积 ) ) =\frac{1}{N}\sum_{i}-\log(\frac{e^{W_{y_i}*{X_i}(卷积)}}{\sum_je^{W_{j}*X_i(卷积)}}) =N1i∑−log(∑jeWj∗Xi(卷积)eWyi∗Xi(卷积)) = 1 N ∑ i − log ( e ∣ ∣ W y i ∣ ∣ ∗ ∣ ∣ x i ∣ ∣ ∗ c o s ( θ y i ) ( 乘 积 ) ∑ j e ∣ ∣ W j ∣ ∣ ∗ ∣ ∣ x i ∣ ∣ ∗ c o s ( θ j ) ( 乘 积 ) ) =\frac{1}{N}\sum_{i}-\log(\frac{e^{||W_{y_i}||*||x_i||*cos(\theta_{y_i})(乘积)}}{\sum_je^{||W_{j}||*||x_i||*cos(\theta_{j})(乘积)}}) =N1i∑−log(∑je∣∣Wj∣∣∗∣∣xi∣∣∗cos(θj)(乘积)e∣∣Wyi∣∣∗∣∣xi∣∣∗cos(θyi)(乘积))
A − S o f t m a x A-Softmax A−Softmax:
L 总 = 1 N ∑ i L i L_{总}=\frac{1}{N}\sum_{i}L_{i} L总=N1i∑Li = 1 N ∑ i − log ( e W y i ∗ X i ( 卷 积 ) ∑ j e W j ∗ X i ( 卷 积 ) ) =\frac{1}{N}\sum_{i}-\log(\frac{e^{W_{y_i}*{X_i}(卷积)}}{\sum_je^{W_{j}*X_i(卷积)}}) =N1i∑−log(∑jeWj∗Xi(卷积)eWyi∗Xi(卷积)) = 1 N ∑ i − log ( e ∣ ∣ W y i ∣ ∣ ∗ ∣ ∣ x i ∣ ∣ ∗ c o s ( θ y i ) ( 乘 积 ) ∑ j e ∣ ∣ W j ∣ ∣ ∗ ∣ ∣ x i ∣ ∣ ∗ c o s ( θ j ) ( 乘 积 ) ) =\frac{1}{N}\sum_{i}-\log(\frac{e^{||W_{y_i}||*||x_i||*cos(\theta_{y_i})(乘积)}}{\sum_je^{||W_{j}||*||x_i||*cos(\theta_{j})(乘积)}}) =N1i∑−log(∑je∣∣Wj∣∣∗∣∣xi∣∣∗cos(θj)(乘积)e∣∣Wyi∣∣∗∣∣xi∣∣∗cos(θyi)(乘积)) = 1 N ∑ i − log ( e ∣ ∣ x i ∣ ∣ ∗ c o s ( θ y i ) ( 乘 积 ) ∑ j e ∣ ∣ x i ∣ ∣ ∗ c o s ( θ j ) ( 乘 积 ) ) =\frac{1}{N}\sum_{i}-\log(\frac{e^{||x_i||*cos(\theta_{y_i})(乘积)}}{\sum_je^{||x_i||*cos(\theta_{j})(乘积)}}) =N1i∑−log(∑je∣∣xi∣∣∗cos(θj)(乘积)e∣∣xi∣∣∗cos(θyi)(乘积)) = 1 N ∑ i − log ( e ∣ ∣ x i ∣ ∣ ∗ c o s ( θ y i ) ( 乘 积 ) e ∣ ∣ x i ∣ ∣ ∗ c o s ( θ y i ) ( 乘 积 ) + ∑ j ≠ y i e ∣ ∣ x i ∣ ∣ ∗ c o s ( θ j ) ( 乘 积 ) ) =\frac{1}{N}\sum_{i}-\log(\frac{e^{||x_i||*cos(\theta_{y_i})(乘积)}}{e^{||x_i||*cos(\theta_{y_i})(乘积)}+\sum_{j\neq y_i}e^{||x_i||*cos(\theta_{j})(乘积)}}) =N1i∑−log(e∣∣xi∣∣∗cos(θyi)(乘积)+∑j̸=yie∣∣xi∣∣∗cos(θj)(乘积)e∣∣xi∣∣∗cos(θyi)(乘积))
上式中的 c o s ( θ y i ) cos(\theta_{y_i}) cos(θyi)可以替换成 ( − 1 ) N c o s ( m θ y i ) − 2 N (-1)^Ncos(m\theta_{y_i})-2N (−1)Ncos(mθyi)−2N。理由上面说明了哈!
然后 A M − S o f t m a x AM-Softmax AM−Softmax和 c o s − F a c e cos-Face cos−Face出场了,把上面的 c o s ( θ ) cos(\theta) cos(θ)变成 c o s ( θ ) − m cos(\theta)-m cos(θ)−m。所以式子就变成了:
L 总 = 1 N ∑ i L i = 1 N ∑ i − log ( e s ∗ ( c o s ( θ y i , i ) − m ) e s ∗ ( c o s ( θ j , i ) − m ) + ∑ j ≠ y i e s ∗ ( c o s ( θ j , i ) − m ) ) L_{总}=\frac{1}{N}\sum_{i}L_{i}=\frac{1}{N}\sum_{i}-\log(\frac{e^{{s*(cos(\theta_{y_i},i)-m)}}}{{e^{s*(cos(\theta_{j},i)-m)}}+{\sum_{j\neq y_i}e^{s*(cos(\theta_{j},i)-m)}}}) L总=N1i∑Li=N1i∑−log(es∗(cos(θj,i)−m)+∑j̸=yies∗(cos(θj,i)−m)es∗(cos(θyi,i)−m))同时满足: W = W ∣ ∣ W ∣ ∣ W=\frac{W}{||W||} W=∣∣W∣∣W s = x = x ∣ ∣ x ∣ ∣ s=x=\frac{x}{||x||} s=x=∣∣x∣∣x W j ∗ x i = 1 ∗ 1 ∗ c o s ( θ j , i ) = c o s ( θ j , i ) W_j*x_i=1*1*cos(\theta_j,i)=cos(\theta_j,i) Wj∗xi=1∗1∗cos(θj,i)=cos(θj,i)
好处:在于 A − S o f t m a x A-Softmax A−Softmax的倍角计算是要通过倍角公式,反向传播时不方便求导,而只减m反向传播时导数不用变化。作者认为, A − s o f t m a x A-softmax A−softmax是用 m m m乘以 θ θ θ,而 A M − S o f t m a x AM-Softmax AM−Softmax是用 c o s θ cosθ cosθ减去 m m m,这是两者的最大不同之处:一个是角度距离,一个是余弦距离。使用传统的Softmax的时候,角度距离和余弦距离是等价的,即: c o s ( θ 1 ) = c o s ( θ 2 ) − − > θ 1 = θ 2 cos(\theta_1)=cos(\theta_2)-->\theta_1=\theta_2 cos(θ1)=cos(θ2)−−>θ1=θ2但是当我们试图要推动决策边界的时候,角度距离和余弦距离就有所不同了。最终的决策边界是和余弦相关的,根据cos的性质,优化角度距离比优化余弦距离更有效果,因为余弦距离相对更密集。之所以选择 c o s θ − m cosθ-m cosθ−m而不是 c o s ( θ − m ) cos(θ-m) cos(θ−m),这是因为我们从网络中得到的是权重 W W W和特征 x x x的内积,如果要优化 c o s ( θ − m ) cos(θ-m) cos(θ−m)那么会涉及到 a r c c o s arccos arccos操作,计算量过大。论文里写的真棒!
8、ArcFace/Insight Face
来自于2018年论文:
A r c F a c e : A d d i t i v e A n g u l a r M a r g i n L o s s f o r D e e p F a c e R e c o g n i t i o n ArcFace: \ Additive \ Angular \ Margin \ Loss \ for \ Deep \ Face \ Recognition ArcFace: Additive Angular Margin Loss for Deep Face Recognition,也叫 I n s i g h t F a c e Insight \ Face Insight Face。这个和 A M − S o f t m a x AM-Softmax AM−Softmax类似,前者是余弦角度,这边是变成角度问题。这么做的原因:角度距离比余弦距离在对角度的影响更加直接。
在二分类情况下,对于类别1, A r c F a c e ArcFace ArcFace的边界决策函数为:
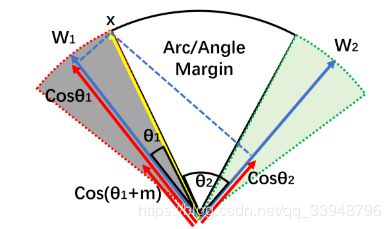
9、小结一下
10、参考链接
- https://blog.csdn.net/u014380165/article/details/76946339
- https://blog.csdn.net/lucifer_zzq/article/details/81236174
- https://zhuanlan.zhihu.com/p/23444100
- https://zhuanlan.zhihu.com/p/41479655
- https://www.cnblogs.com/heguanyou/p/7503025.html
- https://blog.csdn.net/wfei101/article/details/79518017
- https://www.jianshu.com/p/c2653bf83584
- https://blog.csdn.net/fire_light_/article/details/79602310
- https://blog.csdn.net/Fire_Light_/article/details/79602705
- https://blog.csdn.net/wfei101/article/details/80700325


