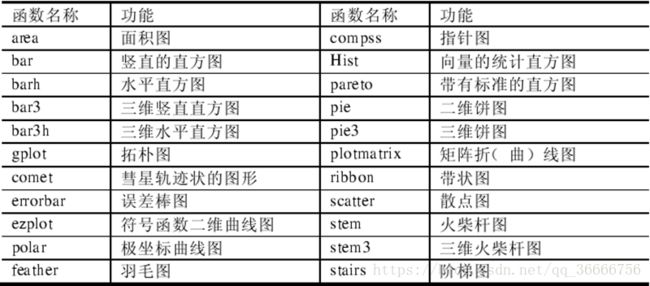
MATLAB基础（二）矩阵运算与可视化作图

                                                                                              常见矩阵生成函数

zeros(m,n)	生成一个 m 行 n 列的零矩阵，m=n 时可简写为 zeros(n)
ones(m,n)	生成一个 m 行 n 列的元素全为 1 的矩阵,  m=n 时可写为 ones(n)
eye(m,n)	生成一个主对角线全为 1 的 m 行 n 列矩阵, m=n 时可简写为 eye(n)，即为 n 维单位矩阵
diag(X)	若 X 是矩阵，则 diag(X) 为 X 的主对角线向量 若 X 是向量，diag(X) 产生以 X 为主对角线的对角矩阵
tril(A)	提取一个矩阵的下三角部分
triu(A)	提取一个矩阵的上三角部分
rand(m,n)	产生 0～1 间均匀分布的随机矩阵 m=n 时简写为 rand(n)
randn(m,n)	产生均值为0，方差为1的标准正态分布随机矩阵 m=n 时简写为 randn(n)
其它特殊矩阵生成函数：magic、hilb、pascal

                                                                                  数组（矩阵）运算

1） 数组的加和减（+，-）

（2） 数组的乘和除（*, .*, /, \）

*矩阵相乘：前一个矩阵的列数等于后一个矩阵的行数才可以相乘。转置：b' ,列如转置是将三行两列转换为两行三列。

*点乘：要求同行同列要相同。左除/ 要求行数相同，右除\要求列数相同。

（3） 数组的乘方（^2）

（4） 数组的逆矩阵（inv(A)）

（5） 矩阵的秩(rank(A))

（6） 矩阵的特征值与特征向量（eig(A)）

（7） 矩阵的行最简形（rref(A)）

（8） 矩阵的行列式（det(A)）

                                                                              Matlab图形可视化

A、二维平面图形与坐标系

用命令 plot(x,y)绘制函数 y=cos(x)在一个周期内的图形。

                      x=0:0.01:2*pi;  

                      y=cos(x);  

                      plot(x,y)

    在同一图形窗口中用命令 plot(x,y)绘出正弦余弦函数的图形。

                      x=0:0.01:2*pi;  

                      y=[sin(x);cos(x)];  

                      plot(x,y)

2.线型和颜色

plot 函数可以设置曲线的线段类型、定点标记和线段颜色。

调用格式：plot(x,y,s) ，s 为类型说明参数，是字符串。

Øs 字符串可以是三种类型的符号之一，也可以是线型与颜色和定点标记与颜色的组合；

Ø如果没有 s 参数，plot 将使用缺省设置（实线，前七种颜色顺序着色）绘制曲线；

Ø在当前坐标系中绘图时，每调入一次绘图函数，MATLAB将擦掉坐标系中已有的图形对象。可以用 hold on 命令在一个坐标系中增加新的图形对象。注意MATLAB会根据新图形的大小，重新改变坐标系的比例。

用不同的线型和标注来绘制两条曲线。

      t1=0:0.1:2*pi;

      t2=0:0.1:6;

      y1=sin(t1);

      y2=sqrt(t2);

      plot(t1,y1,'hb',t2,y2,'--g')                      

 

3. 图形窗口的分割

        有时需要在一个图形窗口中显示几幅图，以便对几个函数进行直观、便捷的比较。由于每个绘图命令在绘制数据图像时都会将已有图形覆盖掉，而用 hold 命令不能实现同时显示几个不同坐标尺寸下的图形，用 figure 命令再创窗口又很难同时比较由不同的数据绘得的图像。

        实现在同一个窗口中同时显示多个图像的命令subplot。

使用格式为：

                                            subplot(m，n，i)

其含义为  ：把图形窗口分割为 m 行 n 列子窗口，然后选定第 i 个窗口为当前窗口。

subplot 命令不仅用于二维图形，对三维图形一样适用。其本质是将 figure 窗口分为几个区域，再在每个区域内分别绘图。

用 subplot 函数把两种不同的图形综合在一个图形窗口中。

subplot(2,2,1)

t=0.1:0.1:2*pi;

y=sin(t);

semilogx(t,y)

grid on 

subplot(2,2,2)

t=0:0.1:4*pi;

y=sin(t);

plot(t,y)

subplot(2,2,3)

x=1:0.01:5;

y=exp(x);

plot(x,y,x,y,’semilogx’,’plot’) 

subplot(2,2,4)

x=1:0.1:10;

y=sqrt(x);

plot(x,y,’:rd’)

 

4. 坐标系的调整

实现坐标系的调整的命令是 axis 函数。

调用格式为： axis([xmin,xmax,ymin,ymax,zmin,zmax])

坐标的最小值（ xmin,ymin,zmin）必须小于相应的最大值（ xmax,ymax,zmax），否则会出错。

自动坐标系与用 axis 函数调整后的坐标系的比较。

subplot(2,1,1)

t=0:0.1:4*pi;

y=sin(t);

plot(t,y) 

subplot(2,1,2)

t=0:0.1:4*pi;

y=sin(t);

plot(t,y)

axis([0,max(t),min(y),max(y)])

B、三维绘图

1. 三维曲线绘图命令

三维函数 plot3主要用来表现单参数的三维曲线，与二维绘图函数 plot 相比，只多了第三维数据。

其调用格式为：

plot3(X1,Y1,Z1,s1,X2,Y2,Z2,s2,…)

参数的含义如下：

ØXn、Yn、Zn：第一到三维数据，是尺寸相等的向量/矩阵；

Øs、s1、s2：是字符串，用来设置线型、颜色、数据点标记。

x、y、z 是向量时，plot3 命令的使用

t=0:0.1:8*pi;

plot3(sin(t),cos(t),t)

title(’绘制螺旋线’)  %用命令 title 对图形主题进行标注

xlabel(’sin(t)’)        

ylabel(’cos(t)’)

zlabel(’t’)    

 %命令 zlabel 用来指定 z 轴的数据名称

grid on

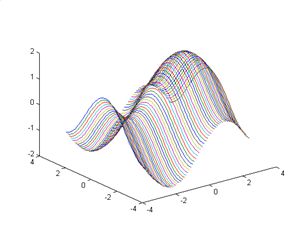
x、y、z 都是矩阵时，plot3 命令的使用

[X,Y]=meshgrid(-pi:0.1:pi);

Z=sin(X)+cos(Y);

plot3(X,Y,Z)

 

2.三维曲面绘图命令

        为了绘制定义在平面区域D=[x0,xm]×[y0,yn]上的三维曲面z=f(x,y) ，首先将[x0,xm]在 x 方向分成 m 份，将[y0,yn]在 y 方向分成 n 份，由各划点分别作平行于坐标轴的直线，将区域 D 分成 m×n 个小矩形；对于每个小矩形，计算出网格点的函数值，决定出空间中四个顶点（xi,yi,f(xi,yi)），连接四个顶点得到一个空间的四边形片；所有四边形片连在一起构成函数 z=f(x,y)定义在区域 D 上的空间网格曲面。

        因此，三维曲面绘图命令可分为平面网格点的生成、在平面网格基础上绘制三维网格及对三维表面进行处理三个步骤。

a.平面网格点的生成

函数命令meshgrid 用来生成 x-y 平面上的网格点矩阵。

调用形式为：

[X,Y]=meshgrid(x,y)

[X,Y]=meshgrid(x) 等价于[X,Y]=meshgrid(x,x)

参数含义如下：

Øx：是区间[x0,xm]上分划的向量；

Øy：是区间[y0,yn]上分划的向量；

ØX，Y：输出变量矩阵，矩阵 X 的行向量都是向量 x，矩阵 Y 的列向量都是向量 y。

函数 meshgrid 将由两个向量决定的区域转换为对应的网格点矩阵。

函数                            ，定义区域为[-2，2]×[-2，2]。生成网格并计算其网格点上的函数值。

[X,Y] = meshgrid(-2:2:2, -2:2:2);

[X,Y]       %将划分结果输出至矩阵

ans =        

-2          0          2        -2        -2        -2

-2          0          2         0          0          0        

-2          0          2         2          2          2

Z = X .* exp(-X.^2 - Y.^2);    %计算网格点上的函数值赋予变量

Z

Z =      

-0.0007                  0        0.0007      

-0.0366                  0        0.0366      

-0.0007                  0        0.0007

 

用 mesh 命令绘制上例中的网格曲面。

 [X,Y] = meshgrid(-2:.2:2, -2:.2:2);

 Z = X .* exp(-X.^2 - Y.^2);

 mesh(Z)

用 mesh 命令绘制上例中的网格曲面。

 [X,Y] = meshgrid(-2:.2:2, -2:.2:2);

 Z = X .* exp(-X.^2 - Y.^2);

 mesh(Z)

c.三维表面命令 surf

函数 surf 可实现对网格曲面片进行着色，将网格曲面转化为实曲面。surf 命令的调用格式与 mesh 相同。

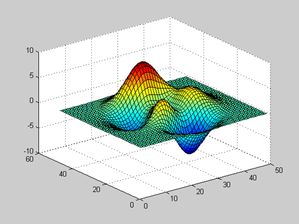
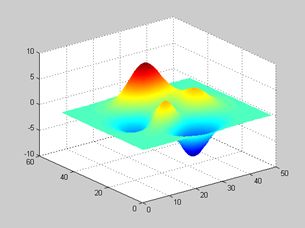
利用三维网格表面命令 surf 绘制图形。

z=peaks;    %绘制山峰的图像，将函数值赋予变量z

 surf(z)  ;   %对山峰的图像进行着色处理

shading interp  %函数 shading 改变着色方式

a.柱面的表达cylinder

cylinder命令中，柱面的轴线定义为 z 轴，只要给出母线的描述就可完成一个柱面。

调用格式为：

Ø[X,Y,Z] = cylinder(R,N)；

Ø[X,Y,Z] = cylinder(R)：缺省值 N=20；

Ø[X,Y,Z] = cylinder：缺省值 N=20，R=[1，1]。

R：是一描述柱面母线的向量；

N：是旋转柱面上的分割线条数；

[X,Y,Z] ：是返回的x,y,z坐标向量。

绘制一个柱面。

   t=pi:0.01:3*pi;

   r=sin(t)+t;

   cylinder(r,30)

   shading interp 

b.球面的表达sphere

调用格式为：

Ø[X,Y,Z]=sphere(N)：产生一个（ N+1）×（ N+1）×（ N+1）的矩阵，然后用函数 surf 命令绘制一个单位的球面，N 为设置分割线的条数；

Ø[X,Y,Z] = sphere：缺省

值 N = 20。

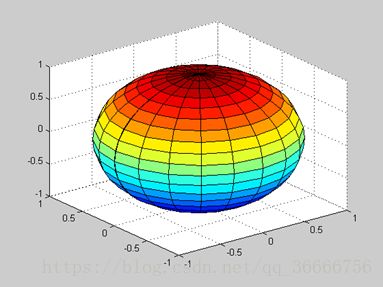
画一个球面。

 [X,Y,Z]=sphere;

  surf(X,Y,Z)

 

四、特殊图形绘制

为了将抽象的数据表达得更形象，除了绘制二维、三维图形外，还要用到直方图、面积图、饼图等特殊图形。

 

1.面积图命令 area

表现各个不同部分对整体所作的贡献

Øarea(X,Y)：与 plot 的命令的使用方法相似，将连线图到 x 轴的那部分填上了颜色；

Øarea(Y)：缺省值 X=1:SIZE(Y)；

Øarea(X,Y,LEVEL)或 area(Y,LEVEL)：填色部分为由连线图到 y=level 的水平线之间的部分。

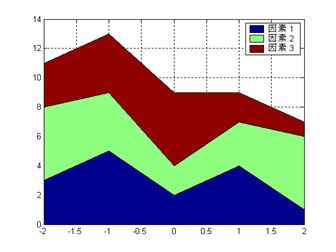
绘制一面积图

X=-2:2;

Y=[3,5,2,4,1;5,4,2,3,5;3,4,5,2,1];

area(X',Y')

legend('因素 1','因素 2','因素 3')

grid on

2.直方图命令 bar

直方图常用于统计数据的作图， 有bar、bar3、barh 和 bar3h几种函数，其调用格式类似。以函数 bar 为例：

Øbar(X,Y)：X 是横坐标向量，Y 可以是向量或矩阵。Y 是向量时，每一个元素对应一个竖条；Y 是 m 行 n 列矩阵时，将画出 m 组竖条，每组包括 n 个竖条；

Øbar(Y)：横坐标使用缺省值 X=1:M；

Øbar(X,Y,WIDTH)  或 bar(Y,WIDTH)：用 WIDTH 指定竖条的宽度，如果 WIDTH＞1，条与条之间将重合。缺省宽度为 0.8；

Øbar(...,’grouped’)：产生缺省的组合直方图；

Øbar(...,’stacked’)：产生累积的直方图；

Øbar(...,linespec)：指定条的颜色；

ØH = bar(...)：返回条形图对象的句柄。

用绘制直方图的几种命令绘制直方图。

X=-2:2;

Y=[3,5,2,4,1;5,4,2,3,5;3,4,5,2,1];

subplot(2,2,1)

bar(X,Y','r')

xlabel('x')

ylabel('y')

colormap(cool)

subplot(2,2,2)

barh(X,Y','grouped')

xlabel('y')

ylabel('x')

colormap(cool)

subplot(2,2,3)

bar(X,Y','stacked')

xlabel('x')

ylabel('\Sigma y')

colormap(summer)

subplot(2,2,4)

barh(X,Y','stacked')

xlabel('y');ylabel('\Sigma x')

colormap(summer)

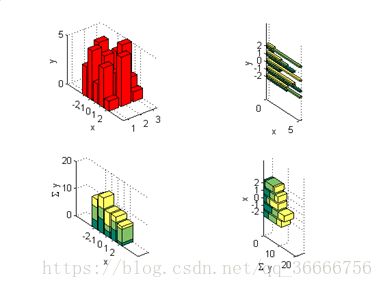
绘制三维直方图。

X=-2:2;

Y=[3,5,2,4,1;5,4,2,3,5;3,4,5,2,1];

subplot(2,2,1)

bar3(X,Y','r')

zlabel('y')

ylabel('x')

colormap(cool)

subplot(2,2,2)

bar3h(X,Y','grouped')

ylabel('x')

zlabel('y')

colormap(cool)

subplot(2,2,3)

bar3(X,Y','stacked')

ylabel('x')

zlabel('\Sigma y')

colormap(summer)

subplot(2,2,4)

bar3h(X,Y’,’stacked’)

zlabel(’x’)

ylabel(’\Sigma y’)

colormap(summer)

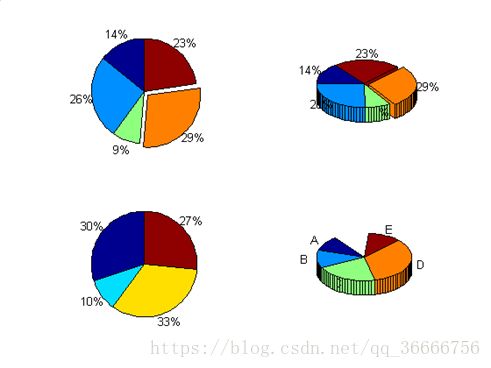
3.饼图命令 pie

饼图又叫扇形图，用于显示向量中元素所占向量元素总和的百分比。 pie 和 pie3分别用于绘制二维和三维饼图。

调用格式：

Øpie(X)：向量 X 的饼图。把 X 的每一个元素在所有元素总和中占的比例表达出来；

Øpie(X,EXPLODE)：向量EXPLODE（和向量X长度相等）用于指定饼图中抽出一部分的块（非零值对应的块）；

Øpie(...,LABELS)：LABELS 是用于标注饼图的字符串数组，其长度必须和向量 X相等；

ØH = pie(...)：返回包括饼图和文本对象句柄。

3.饼图命令 pie

饼图又叫扇形图，用于显示向量中元素所占向量元素总和的百分比。 pie 和 pie3分别用于绘制二维和三维饼图。

调用格式：

Øpie(X)：向量 X 的饼图。把 X 的每一个元素在所有元素总和中占的比例表达出来；

Øpie(X,EXPLODE)：向量EXPLODE（和向量X长度相等）用于指定饼图中抽出一部分的块（非零值对应的块）；

Øpie(...,LABELS)：LABELS 是用于标注饼图的字符串数组，其长度必须和向量 X相等；

ØH = pie(...)：返回包括饼图和文本对象句柄。

五、坐标轴的调整和图形的标注

1.坐标轴调整命令

2.图形标注

a.坐标轴和图形标题标注

Ø标注坐标轴 x、y 和 z 的命令函数为 xlabel、ylabel 和 zlabel ，调用格式为：

§xlabel(’text’)

§xlabel(’text’,’Property1’,PropertyValue1,’Property2’,PropertyValue2,...)

§H = xlabel(...)  返回坐标轴标注的句柄。

其中，’text’是要添加的标注文本。’Property’是文本的属性名，’PropertyValue’是属性值（所用字体、大小、标注角度等）。

Ø图形加标题的函数为 title，其调用格式与坐标轴标注类似。

 

b. 图例的标注

legend命令实现不同图例的说明。其调用格式为：

legend(string1,string2,string3, ...)  

legend(string1,string2,string3,...,Pos)  

按顺序把字符串添加到相应的曲线线型符号之后；Pos对图例的位置作出设置和调整：

Ø0 = 自动把图例置于最佳位置（ 和图中曲线重复最少）；

Ø1 =  置于图形窗口的右上角（ 缺省值）；

Ø2 =  置于图形窗口的左上角；

Ø3 =  置于图形窗口的左下角；

Ø4 =  置于图形窗口的右下角；

Ø-1 =  置于图形窗口的右侧（ 外部）。

 

3.控制分格线

对二维和三维图形都适用。

有三种用法：

Øgrid on：打开分格线控制开关，绘制的图形都带有分格线；

Øgrid off：关闭分格线控制开关，绘制的图形都不带分格线；

Øgrid：用于实现分格线绘制切换。

Øhold on :在原来图的基础上继续对另外的图进行绘制