SVM算法理解以及编程练习

支持向量机

支持向量机就算法作为机器学习的经典算法，从被提出后快速发展，在很多场景和领域都取得了非常好的效果，同时兼有速度块、支持数据量大等特点使其在工程实践中得到广泛应用。

首先我们先来看一个3维的平面方程：Ax+By+Cz+D=0
这就是我们中学所学的，从这个方程我们可以推导出二维空间的一条直线：Ax+By+D=0

那么，依次类推，更高维的空间叫做一个超平面。
二维空间的几何表示：

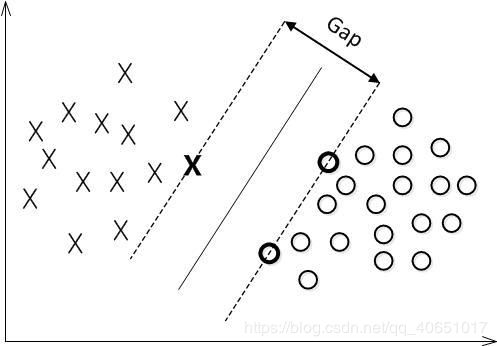
SVM的目标是找到一个超平面，这个超平面能够很好的解决二分类问题，所以先找到各个分类的样本点离这个超平面最近的点，使得这个点到超平面的距离最大化，最近的点就是虚线所画的。由以上超平面公式计算得出大于1的就属于打叉分类，如果小于0的属于圆圈分类。

如何找到超平面

在超平面wx+b=0确定的情况下，|wx+b|能够表示点x到距离超平面的远近，而通过观察wx+b的符号与类标记y的符号是否一致可判断分类是否正确，所以，可以用(y(w*x+b))的正负性来判定或表示分类的正确性。于此，我们便引出了函数间隔（functional margin）的概念。定义函数间隔（用γ表示)为：

但是这个函数间隔有个问题，就是我成倍的增加w和b的值，则函数值也会跟着成倍增加，但这个超平面没有改变。所以有函数间隔还不够，需要一个几何间隔。

几何间隔
我们把w做一个约束条件，假定对于一个点 x ，令其垂直投影到超平面上的对应点为 x0 ，w 是垂直于超平面的一个向量，为样本x到超平面的距离，如下图所示：

最大间隔分类器

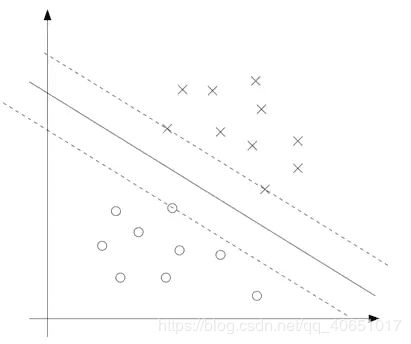
对一个数据点进行分类，当超平面离数据点的“间隔”越大，分类的确信度（confidence）也越大。所以，为了使得分类的确信度尽量高，需要让所选择的超平面能够最大化这个“间隔”值。这个间隔就是下图中的Gap的一半。

代码练习理解

代码1

import numpy as np
import matplotlib.pyplot as plt

from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

iris = datasets.load_iris()

X = iris.data
y = iris.target

X = X [y<2,:2] #只取y<2的类别，也就是0 1 并且只取前两个特征
y = y[y<2] # 只取y<2的类别

# 分别画出类别0和1的点
plt.scatter(X[y==0,0],X[y==0,1],color='red') 
plt.scatter(X[y==1,0],X[y==1,1],color='blue')
plt.show()

# 标准化
standardScaler = StandardScaler()

standardScaler.fit(X) #计算训练数据的均值和方差
X_standard = standardScaler.transform(X) #再用scaler中的均值和方差来转换X，使X标准化

svc = LinearSVC(C=1e9) #线性SVM分类器
svc.fit(X_standard,y) # 训练svm

这是未经过标准化的原始数据点分布

代码2

绘制决策边界

def plot_decision_boundary(model, axis):
    
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]
    
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)
    
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)


# 绘制决策边界
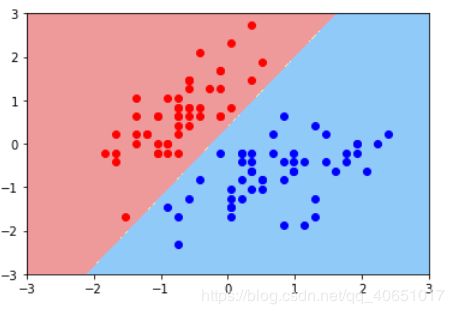
plot_decision_boundary(svc,axis=[-3,3,-3,3]) # x,y轴都在-3到3之间
# 绘制原始数据
plt.scatter(X_standard[y==0,0],X_standard[y==0,1],color='red') 
plt.scatter(X_standard[y==1,0],X_standard[y==1,1],color='blue')
plt.show()

上面说了CCC是控制正则项的重要程度，这里我们再次实例化一个svc，并传入一个较小的C。

代码3

svc2 = LinearSVC(C=0.01)
svc2.fit(X_standard,y)
plot_decision_boundary(svc2,axis=[-3,3,-3,3]) # x,y轴都在-3到3之间
# 绘制原始数据
plt.scatter(X_standard[y==0,0],X_standard[y==0,1],color='red') 
plt.scatter(X_standard[y==1,0],X_standard[y==1,1],color='blue')
plt.show()

可以很明显的看到和第一个决策边界的不同，在这个决策边界汇总，有一个红点是分类错误的。
C越小容错空间越大。

代码4

使用多项式特征和核函数

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

X, y = datasets.make_moons() #使用生成的数据
print(X.shape) # (100,2)
print(y.shape) # (100,)

生成月亮数据集

plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

X, y = datasets.make_moons(noise=0.15,random_state=777) #随机生成噪声点，random_state是随机种子，noise是方差

plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

多项式特征的SVM来对它进行分类。

from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline

def PolynomialSVC(degree,C=1.0):
    return Pipeline([
        ("poly",PolynomialFeatures(degree=degree)),#生成多项式
        ("std_scaler",StandardScaler()),#标准化
        ("linearSVC",LinearSVC(C=C))#最后生成svm
    ])

poly_svc = PolynomialSVC(degree=3)
poly_svc.fit(X,y)

plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

我们可以看到，生成的边界不再是线性的直线了。

使用核技巧来对数据进行处理，使其维度提升，使原本线性不可分的数据，在高维空间变成线性可分的。再用线性SVM来进行处理。

from sklearn.svm import SVC

def PolynomialKernelSVC(degree,C=1.0):
    return Pipeline([
        ("std_scaler",StandardScaler()),
        ("kernelSVC",SVC(kernel="poly")) # poly代表多项式特征
    ])

poly_kernel_svc = PolynomialKernelSVC(degree=3)
poly_kernel_svc.fit(X,y)

plot_decision_boundary(poly_kernel_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

可以看到这种方式也生成了一个非线性的边界。

这里SVC(kernel=“poly”)有个参数是kernel，就是核函数.

害！就这样吧…