向量vector(2)
目录
1.3 构造与析构
1.3.1 默认构造方法
1.3.2 基于复制的构造方法
1.3.3 析构方法
1.4 动态空间管理
1.4.1 静态空间管理
1.4.2 可扩充向量
1.4.3 扩容
1.4.4 分摊分析
1.4.4.1 递增式扩容
1.4.4.2 加倍式扩容
1.4.4.3 平均分析与分摊分析
1.4.5 缩容
1.5 常规向量
1.5.1 直接引用元素
1.5.2 置乱器
1.5.2.1 置乱算法
1.5.2.2 区间置乱接口
1.5.3 判等器与比较器
1.3 构造与析构
向量结构中在内部维护一个元素类型为T的私有元素_elem[ ];容量为_capacity;有效元素的数量(即向量当前的实际规模)由_size指示。向量对象的构造与析构,将围绕这些私有变量和数据区的初始化与销毁展开。
1.3.1 默认构造方法
Vector ( int c = DEFAULT_CAPACITY, int s = 0, T v = 0 ) //容量为c、规模为s、所有元素初始为v
{ _elem = new T[_capacity = c]; for ( _size = 0; _size < s; _elem[_size++] = v ); } //s<=c根据创建者指定的初始容量,向系统申请空间,以创建私有数组_elem[];若容量未明确,则使用默认值DEFAULT_CAPACITY。初始的向量尚未有任何元素,将_size初始化为0。
1.3.2 基于复制的构造方法
template //元素类型
void Vector::copyFrom ( T const* A, Rank lo, Rank hi ) { //以数组区间A[lo, hi)为蓝本复制向量
_elem = new T[_capacity = 2 * ( hi - lo ) ]; _size = 0; //分配空间,规模清零
while ( lo < hi ) //A[lo, hi)内的元素逐一
_elem[_size++] = A[lo++]; //复制至_elem[0, hi - lo)
} 向量的另一个典型的创建方式就是以某个已有的向量或者数组为蓝本,进行(局部或者整体的)复制。copyFrom()首先根据复制区间的边界,换算成新向量的初始规模;再以双倍的容量,为内部数组_elem[ ]申请空间。最后通过一趟迭代,完成区间A[ lo, hi )内各元素的顺次复制。
但是由于向量内部含有动态分配的空间,默认的运算符“=”不足以支持向量之间的直接赋值。之后将以二维向量形式实现图邻接表,其主向量中的每一元素本身都是一维向量,通过默认赋值运算符,并不能复制向量内部的数据区,需要重载向量的赋值运算符。
template Vector::operator= ( Vector const& V) { //重载
if( _elem )
delete []_elem; //释放原有内容
copyFrom( V._elem, 0, V.size() ); //整体复制
return *this; //返回当前对象的引用,以便链式赋值
} 1.3.3 析构方法
// 析构函数
~Vector() { delete [] _elem; } //释放内部空间只需要释放用于存放元素的内部数组_elem[ ],将其占用的空间交还操作系统。_capacity和_size之类的内部变量无需做任何处理,它们将作为向量对象自身的一部分被系统回收,此后既无需也无法被引用。
1.4 动态空间管理
1.4.1 静态空间管理
内部数组空间所占物理空间的容量,若在向量的生命期内不允许调整,则称作静态空间管理策略。
上溢 : 容量固定时,在之后的某个时刻无法加入更多新的元素
装填因子 : 向量实际规模与其内部数组容量的比值 ( _size/_capacity )
1.4.2 可扩充向量
1.4.3 扩容
template void Vector::expand() { //向量空间不足时扩容
if ( _size < _capacity ) return; //尚未满员时,不必扩容
if ( _capacity < DEFAULT_CAPACITY ) _capacity = DEFAULT_CAPACITY; //不低于最小容量
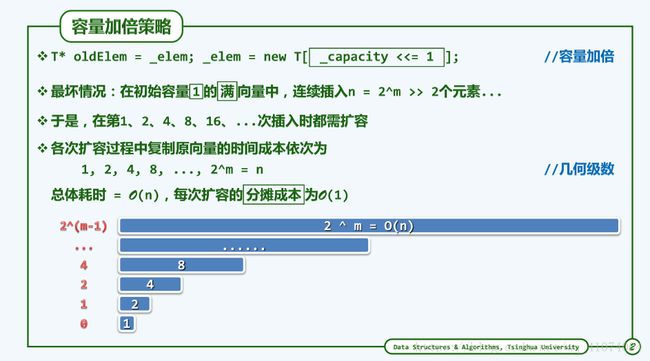
T* oldElem = _elem; _elem = new T[_capacity <<= 1]; //容量加倍
for ( int i = 0; i < _size; i++ )
_elem[i] = oldElem[i]; //复制原向量内容(T为基本类型,或已重载赋值操作符'=')
/*DSA*/ //printf("\n_ELEM [%x]*%d/%d expanded and shift to [%x]*%d/%d\n", oldElem, _size, _capacity/2, _elem, _size, _capacity);
delete [] oldElem; //释放原空间
}
在调用insert()接口插入新元素之前,都要先调用该算法,检查内部数组的可用容量。一旦当前数据区已满
(_size == _capacity),则将原数组替换为一个更大的数组。
新数组的地址由操作系统分配,与原数据区没有直接的关系。这种情况下,若直接引用数组,往往会导致共同指向原数组的其他指针失效,成为野指针( wild pointer );而经过封装为向量之后,即可继续准确地引用各元素,从而有效地避免野指针的风险。
1.4.4 分摊分析
1.4.4.1 递增式扩容
1.4.4.2 加倍式扩容
效率对比 :
1.4.4.3 平均分析与分摊分析
1.4.5 缩容
template void Vector::shrink() { //装填因子过小时压缩向量所占空间
if ( _capacity < DEFAULT_CAPACITY << 1 ) return; //不致收缩到DEFAULT_CAPACITY以下
if ( _size << 2 > _capacity ) return; //以25%为界
T* oldElem = _elem; _elem = new T[_capacity >>= 1]; //容量减半
for ( int i = 0; i < _size; i++ ) _elem[i] = oldElem[i]; //复制原向量内容
delete [] oldElem; //释放原空间
} 缩容就好比扩容的逆操作,分析跟上面扩容基本一致就不再写了。当然,如果就单次扩容或者缩容操作而言,所需时间会高达Ω(n),因此在对单次操作的执行速度极其敏感的场合以上策略不适用,缩容甚至不予考虑。
1.5 常规向量
1.5.1 直接引用元素
为了使向量能像数组那样通过下标访问元素的方式,则需要重载操作符" [ ] "
template T& Vector::operator[] (Rank r) const //重载下标操作符
{ return _elem[r]; } //assert : 0 <= r < _size
1.5.2 置乱器
1.5.2.1 置乱算法
template void permute ( Vector& V ) { //随机置乱向量,使各元素等概率出现于各位置
for ( int i = V.size(); i > 0; i-- ) //自后向前
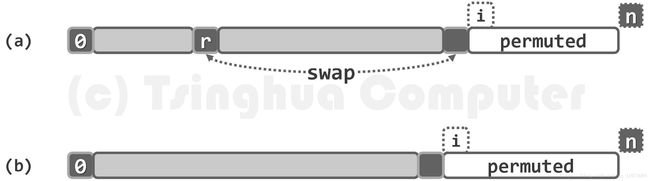
swap ( V[i - 1], V[rand() % i] ); //V[i - 1]与V[0, i)中某一随机元素交换
} 效果如下图所示
在软件测试\仿真模拟等应用中,随机向量的生成都是一项至关重要的基本操作,直接影响到测试的覆盖面或仿真的真实性。使用permute().不仅可以枚举出同一向量所有可能的排列,而且能保证生成各种排列的概率均等。
1.5.2.2 区间置乱接口
template void Vector::unsort ( Rank lo, Rank hi ) { //等概率随机置乱区间[lo, hi)
T* V = _elem + lo; //将子向量_elem[lo, hi)视作另一向量V[0, hi - lo)
for ( Rank i = hi - lo; i > 0; i-- ) //自后向前
swap ( V[i - 1], V[rand() % i] ); //将V[i - 1]与V[0, i)中某一元素随机交换
} 通过该接口,可以均匀地置乱任一向量区间[ lo, hi)内的元素,故通用性有所提高。
1.5.3 判等器与比较器
比对 : 判断两个对象是否相等
比较 : 判断两个对象的相对大小
template static bool lt (T* a, T* b){ return lt ( *a, *b); } //less than
template static bool lt (T& a, T& b){ return a < b; } //less than
template static bool lt (T* a, T* b){ return eq ( *a, *b); } //less than
template static bool lt (T& a, T& b){ return a == b; } //less than