向量vector（3）

目录

 

1.5.4  无序查找

1.5.4.1  判等器

1.5.4.2  顺序查找

1.5.5  插入

1.5.6  删除

1.5.6.1  区间删除 ： remove（ lo, hi ）

1.5.6.2  单元素删除 remove (r)

1.5.7  唯一化

1.5.8  遍历

1.6  有序向量

1.6.1  比较器

1.6.2  有序性甄别

1.6.3  唯一化

---

1.5.4  无序查找

1.5.4.1  判等器

在向量模板类Vector(见前面的  向量vector（1）)中的Vector::find（e）接口，功能是“查找与数据对象e相等的元素”。这也表示，向量元素可通过相互比对判等----例如，元素类型T或为基本类型，或已重载操作符“==”或“！=”。这类仅支持比对，但未必支持比较的向量，称为无序向量（unsorted vector）。

1.5.4.2  顺序查找

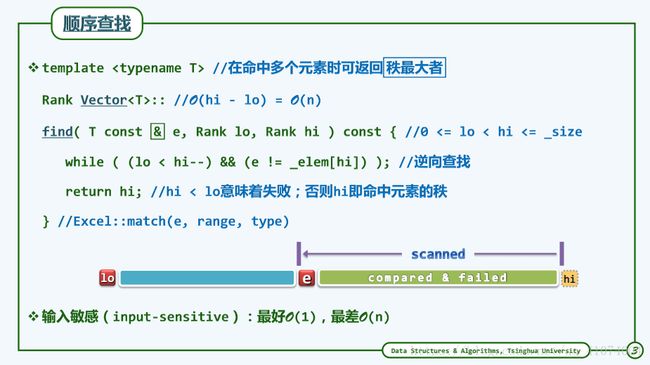
template  //无序向量的顺序查找：返回最后一个元素e的位置；失败时，返回lo - 1
Rank Vector::find ( T const& e, Rank lo, Rank hi ) const { //assert: 0 <= lo < hi <= _size
   while ( ( lo < hi-- ) && ( e != _elem[hi] ) ); //从后向前，顺序查找
   return hi; //若hi < lo，则意味着失败；否则hi即命中元素的秩
}

从后往前逐一取出各个元素并与目标元素e进行比对，直至发现与之相等者（查找成功），或者直到检查所有元素后仍未找到相等者（查找失败）。用while循环的控制逻辑由两部分组成，首先判断是否已抵达通配符，再判断当前元素与目标元素是否相等。当前一个判断非真后循环会立刻终止，而不会因为试图引用已越界的秩（-1）而出错。

1.5.5  插入

template  //将e作为秩为r元素插入
Rank Vector::insert ( Rank r, T const& e ) { //assert: 0 <= r <= size
   expand(); //若有必要，扩容
   for ( int i = _size; i > r; i-- ) _elem[i] = _elem[i-1]; //自后向前，后继元素顺次后移一个单元
   _elem[r] = e; _size++; //置入新元素并更新容量
   return r; //返回秩
}

1.5.6  删除

1.5.6.1  区间删除 ： remove（ lo, hi ）

template  int Vector::remove ( Rank lo, Rank hi ) { //删除区间[lo, hi)
   if ( lo == hi ) return 0; //出于效率考虑，单独处理退化情况，比如remove(0, 0)
   while ( hi < _size ) _elem[lo++] = _elem[hi++]; //[hi, _size)顺次前移hi - lo个单元
   _size = lo; //更新规模，直接丢弃尾部[lo, _size = hi)区间
   shrink(); //若有必要，则缩容
   return hi - lo; //返回被删除元素的数目
}

1.5.6.2  单元素删除 remove (r)

利用上面的区间删除接口,通过重载实现另一个同名接口remove(r)。

template  T Vector::remove ( Rank r ) { //删除向量中秩为r的元素，0 <= r < size
   T e = _elem[r]; //备份被删除元素
   remove ( r, r + 1 ); //调用区间删除算法，等效于对区间[r, r + 1)的删除
   return e; //返回被删除元素
}

1.5.7  唯一化

在一些应用中,在进一步处理之前都要求数据元素互异,唯一化就是剔除其中的重复元素

template  int Vector::deduplicate() { //删除无序向量中重复元素（高效版）
   int oldSize = _size; //记录原规模
   Rank i = 1; //从_elem[1]开始
   while ( i < _size ) //自前向后逐一考查各元素_elem[i]
      ( find ( _elem[i], 0, i ) < 0 ) ? //在其前缀中寻找与之雷同者（至多一个）
      i++ : remove ( i ); //若无雷同则继续考查其后继，否则删除雷同者
   return oldSize - _size; //向量规模变化量，即被删除元素总数
}

1.5.8  遍历

在很多算法中,需要将向量看成一个整体,对其中所有元素实施某种统一操作,比如输出向量中所有的元素,需要设置相应的遍历接口。

template  void Vector::traverse ( void ( *visit ) ( T& ) ) //借助函数指针机制
{ for ( int i = 0; i < _size; i++ ) visit ( _elem[i] ); } //遍历向量

template  template  //元素类型、操作器
void Vector::traverse ( VST& visit ) //借助函数对象机制
{ for ( int i = 0; i < _size; i++ ) visit ( _elem[i] ); } //遍历向量

一种是局部遍历,一种是全局遍历。

1.6  有序向量

如果向量中所有元素不仅按线性次序存放,而且其数值大小也按此次序单调分布,则称为有序向量( sorted vector).

1.6.1  比较器

除了与无序向量一样需要支持元素之间的"判等"操作,有序向量的定义隐含了更强的先决条件: 各元素之间必须能够比较大小 

1.6.2  有序性甄别

原理与冒泡排序算法相同,顺序扫描整个向量,逐一比较每一对相邻元素--向量元素已经有序,当且仅当它们都是顺序的.

template  int Vector::disordered() const { //返回向量中逆序相邻元素对的总数
   int n = 0; //计数器
   for ( int i = 1; i < _size; i++ ) //逐一检查_size - 1对相邻元素
      if ( _elem[i - 1] > _elem[i] ) n++; //逆序则计数
   return n; //向量有序当且仅当n = 0
}

 

1.6.3  唯一化

方法为清除无序向量中的重复元素

低效版

template  int Vector::uniquify() { //有序向量重复元素剔除算法（低效版）
   int oldSize = _size; int i = 1; //当前比对元素的秩，起始于首元素
   while ( i < _size ) //从前向后，逐一比对各对相邻元素
      _elem[i - 1] == _elem[i] ? remove ( i ) : i++; //若雷同，则删除后者；否则，转至后一元素
   return oldSize - _size; //向量规模变化量，即被删除元素总数
}

高效版

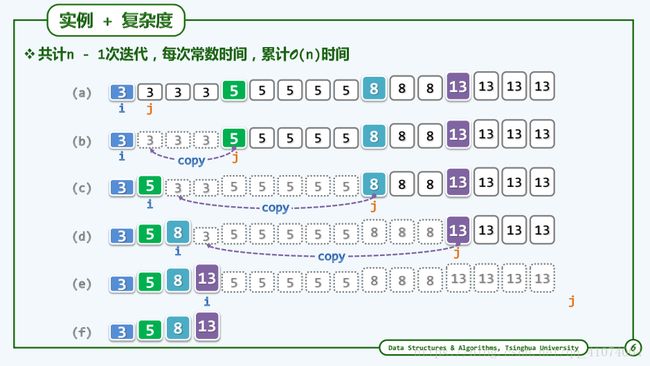
template  int Vector::uniquify() { //有序向量重复元素剔除算法（高效版）
   Rank i = 0, j = 0; //各对互异“相邻”元素的秩
   while ( ++j < _size ) //逐一扫描，直至末元素
      if ( _elem[i] != _elem[j] ) //跳过雷同者
         _elem[++i] = _elem[j]; //发现不同元素时，向前移至紧邻于前者右侧
   _size = ++i; shrink(); //直接截除尾部多余元素
   return j - i; //向量规模变化量，即被删除元素总数
}