向量vector（5）

目录

 

1.7  排序与下节

1.7.1  有序性

1.7.2  排序及其分类

1.7.3  下界

1.7.4  比较树

1.7.4.1  基于比较的分支

1.7.4.2  比较树

1.7.5  估计下界

1.8  排序器

1.8.1  统一入口

1.8.2  冒泡排序

 

1.8.3  归并排序

1.8.3.1  有序向量的二路归并

1.8.3.2  分治策略

1.8.3.3  二路归并接口的实现

---

1.7  排序与下节

1.7.1  有序性

有序性在很多场合都能够极大地提高计算的效率

1.7.2  排序及其分类

算法分类 ：

1.7.3  下界

任一问题在最坏情况下的最低计算成本，就是该问题的复杂度下界

1.7.4  比较树

1.7.4.1  基于比较的分支

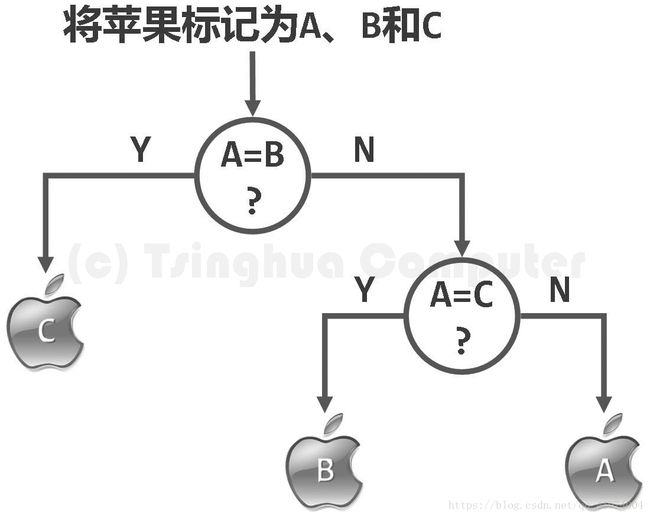
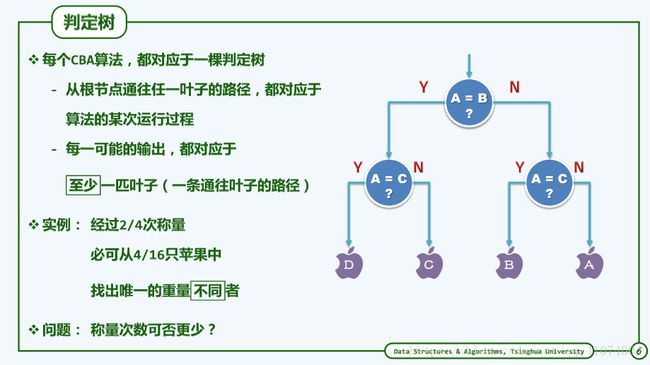
1.7.4.2  比较树

比较树的性质 ：

1. 每一内部节点各对应于一次比对操作
2. 内部节点的左、右分支，分别对应于两种比对结果下的执行方向
3. 叶节点对应于算法某次执行的完整过程及输出
4. 算法的每一运行过程都对应于从根到某一节点的路径

CBA式算法 ： 基于比较式算法

1.7.5  估计下界

见课本P59面

1.8  排序器

1.8.1  统一入口

template  void Vector::sort ( Rank lo, Rank hi ) { //向量区间[lo, hi)排序
   switch ( rand() % 5 ) { //随机选取排序算法。可根据具体问题的特点灵活选取或扩充
      case 1:  bubbleSort ( lo, hi ); break; //起泡排序
      case 2:  selectionSort ( lo, hi ); break; //选择排序（习题）
      case 3:  mergeSort ( lo, hi ); break; //归并排序
      case 4:  heapSort ( lo, hi ); break; //堆排序（稍后介绍）
      default: quickSort ( lo, hi ); break; //快速排序（稍后介绍）
   }
   /*DSA*/ //selectionSort(lo, hi);
}

针对任意合法向量区间的排序需求，定义了以上统一的入口，提供了冒泡、选择、归并、堆、快速排序等多种算法。

1.8.2  冒泡排序

template  //向量的起泡排序
void Vector::bubbleSort ( Rank lo, Rank hi ) //assert: 0 <= lo < hi <= size
{ while ( !bubble ( lo, hi-- ) ); } //逐趟做扫描交换，直至全序

 扫描交换代码如下

template  bool Vector::bubble ( Rank lo, Rank hi ) { //一趟扫描交换
   bool sorted = true; //整体有序标志
   while ( ++lo < hi ) //自左向右，逐一检查各对相邻元素
      if ( _elem[lo - 1] > _elem[lo] ) { //若逆序，则
         sorted = false; //意味着尚未整体有序，并需要
         swap ( _elem[lo - 1], _elem[lo] ); //通过交换使局部有序
      }
   return sorted; //返回有序标志
}

 

1.8.3  归并排序

1.8.3.1  有序向量的二路归并

二路归并:将两个有序序列合并为一个有序序列

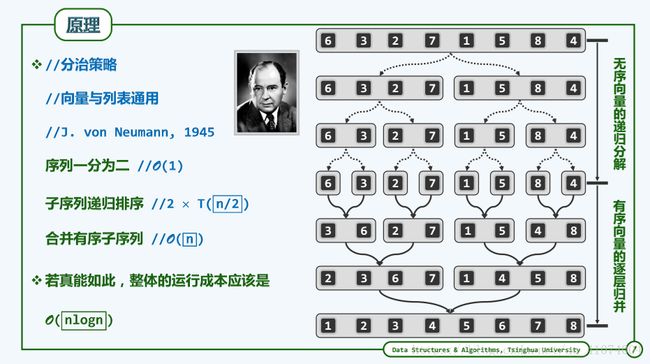
1.8.3.2  分治策略

template  //向量归并排序
void Vector::mergeSort ( Rank lo, Rank hi ) { //0 <= lo < hi <= size
   /*DSA*/printf ( "\tMERGEsort [%3d, %3d)\n", lo , hi );
   if ( hi - lo < 2 ) return; //单元素区间自然有序，否则...
   int mi = ( lo + hi ) / 2; //以中点为界
   mergeSort ( lo, mi ); mergeSort ( mi, hi ); //分别排序
   merge ( lo, mi, hi ); //归并
}

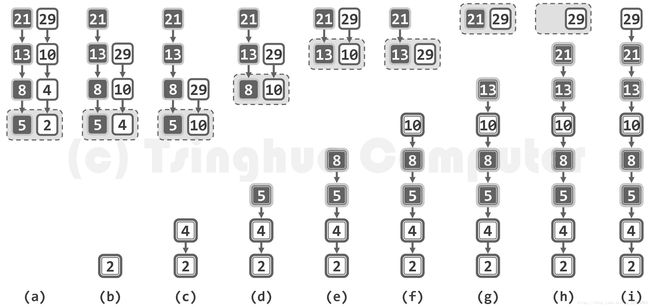
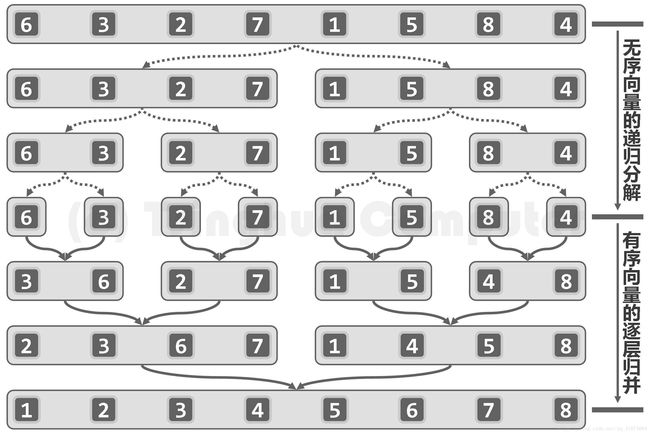
实例:

1.8.3.3  二路归并接口的实现

template  //有序向量的归并
void Vector::merge ( Rank lo, Rank mi, Rank hi ) { //各自有序的子向量[lo, mi)和[mi, hi)
   T* A = _elem + lo; //合并后的向量A[0, hi - lo) = _elem[lo, hi)
   int lb = mi - lo; T* B = new T[lb]; //前子向量B[0, lb) = _elem[lo, mi)
   for ( Rank i = 0; i < lb; B[i] = A[i++] ); //复制前子向量
   int lc = hi - mi; T* C = _elem + mi; //后子向量C[0, lc) = _elem[mi, hi)
   for ( Rank i = 0, j = 0, k = 0; ( j < lb ) || ( k < lc ); ) { //B[j]和C[k]中的小者续至A末尾
      if ( ( j < lb ) && ( ! ( k < lc ) || ( B[j] <= C[k] ) ) ) A[i++] = B[j++];
      if ( ( k < lc ) && ( ! ( j < lb ) || ( C[k] <  B[j] ) ) ) A[i++] = C[k++];
   }
   delete [] B; //释放临时空间B
} //归并后得到完整的有序向量[lo, hi)