计算机组成原理之浮点数
一、浮点数的表示方法:
在计算机中,一个任意进制数N可以可以写成:N=R^e*M
一般来说,变化的数值是M和e。在计算机中只需要存M和e即可,R默认为2。为了使浮点数的表示具有唯一性,需要在运算过程中对浮点数进行规格化操作。于是,制定了IEEE754浮点数表示方法。
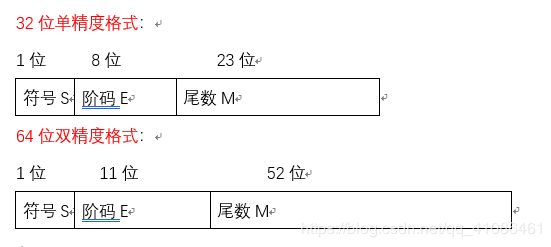
IEEE754标准浮点数的表示方法:
刚刚提到,在计算机中一个任意进制数都可以表示为N=R^e*M
的形式,其中e为指数。在IEEE754浮点数表示形式中,阶码为E。这二者有什么联系和区别呢?
首先,我们应该了解什么是阶码。阶码,也叫做移码。移码就是把-128~+127之间的数字,都平移到0~255范围内,方便比较大小。所以,移码就需要把该指数加127(1023双精度)。即E=e+127(1023)。
移码对两个指数大小的比较和对阶操作(下面进行浮点数的加减的时候会用到)都比较方便。阶码大的指数的值也就大。对阶就是将指数统一,方便进行算数运算。所以,如果给出指数e(真值),那么它在计算机中就是e+127(1023)这样存放的。如果给出存储形式E求真值,那就E-127(1023)。
IEEE754标准中,一个规格化的32位浮点数X的真值可以表示为:X=(-1)^s*(1 . M)*2^(E-127)。其中有个默认的1在整数部分,在计算机中是没有储存的,凡是IEEE754规格化浮点数都是默认整数部分为1,也叫隐含的1。其中,s取0或1,取0时,表示一个正浮点数,取1时,表示一个负浮点数。
特别地,阶码全0和阶码全1用作了两个特殊用途。
- 当阶码全0,尾数也全部为0(8个0)的时候,表示X为0,再结合符号位S,有+0和-0之分。
- 当阶码全1,尾数全0(8个1,255)的时候表示无穷,同样也有+∞和-∞之分。
所以,阶码E能表示的有效范围为1~254。因此,指数e能表示的范围为E-127,也就是-126~+127。
二、浮点数的加减运算:
四个步骤:
- 0操作数的检查
这一个步骤非常简单,就是判断两个操作数是否为0,当其中一个操作数为0的时候,没有必要进行后续的操作了,可以直接得出结果。
- 比较阶码并且完成对阶(重点)
如果两个操作数都不为0,那么就开始完成阶码的大小比较。如果如果两个数的阶码相同,那么就直接进行尾数的加减运算。
否则,必须先让二者的阶码相同才能继续尾数的的运算。两种选择:大的阶码→小的阶码,尾数左移或者小数点右移,小的阶码→大的阶码,尾数右移或者小数点左移。
不过,尾数右移会引起最低有效位的丢失,也就是说,丢掉的是最低位,误差小,左移丢掉的是最高位,误差大。所以,一般选择尾数右移,也就是小的阶码化大的阶码(小的阶码增加)。
让两个操作数的阶码相同的过程就叫做对阶。
- 尾数进行加或减运算
当两个操作数的阶码相同的时候,我们就可以进行尾数的求和运算了。
- 结果规格化
因为尾数是一个小数,超过1就溢出了,所以尾数一定小于1。
由于为了节约存储空间,所以一定要让尾数大于等于0.5,0.5在二进制中的表示为0.1b,所以小数的最高位为1。为什么必须为1呢?
举个简单的例子(二进制表示),0.1*2^0,这个数也可以表示为0.000001*2^5,但是这样表示占据的存储位置比较大,而且1越是往后面移动,指数也要增加,这样一来,指数的存储空间也要增大。所以,对于浮点数尾数的范围为0.5<=| M |<1(十进制)。
因此,结果规格化有一个原则:0.5<=| M |<1。
尾数运算采用双符号位,浮点运算中,尾数求和结果的绝对值大于1(即溢出符号位为01或者10),称为向左破坏了规格化。
双符号位判决法(百度):00表示正号,11表示负号。如果进位将会导致符号位不一致,从而检测出溢出。结果的符号位为01时,称为上溢;为10时,称为下溢。
此时,将尾数运算结果右移用来实现规格化表示,称为向右规格化,简称右规。
如果运算结果的绝对值小于1/2,向右破坏规格化,将尾数结果左移实现规格化表示,称为向左规格化,简称左规。
左规的情况:
- 尾数用原码表示,【S】原=Sf . S1S2…Sn,Sf为符号位。如果尾数未发生溢出,但是S1=0,则向右破坏规格化,需要左规。
- 尾数用补码表示,【S】补=Sf . S1S2…Sn,Sf为符号位。如果尾数未发生溢出,但Sf⊕S1=0,即Sf和S1相同,则向右破坏规格化,需要左规。
比如,,符号位为1,最高数值位为0,化为真值就是11,是规格化的结果,符号位为1,最高数值位为0,化为真值就是11,是规格化结果。
补码化真值的方法就是除符号位按位取反在最低位加一(就和原码化补码的方法一样)。如果实在不清楚原补反码可以在我之前写的定点数的原补反码中查看。
总而言之,尾数用原码来表示,最高数值位为1的时候是规格化的,对于补码而言,符号位与最高数值位相异的时候是规格化的。
- 舍入处理
在对阶或者或者向右规格化时,尾数要向右移位,这样,被右移的尾数的低位部分会被丢掉,从而造成一定的误差,所以要进行舍入的处理。
在十进制中,我们采用的是“四舍五入”,同样,在二进制中,我们是采用“0舍1入”。也就是说,尾数右移的时候,被丢掉的数的最高位是0就舍去,如果是1就将留下的尾数的末位加1。(还有另外一种方法是“恒置一”法,就是不管移掉的数最高位是0还是1,都在保留的尾数的末位加1)
三、浮点数的溢出
A-----最大正数
a-----最小正数
B-----最小负数
b-----最大负数
在机器中,负下溢和正下溢不作处理,因为接近0,直接当作0来处理。
浮点数中,阶码溢出才是真正的溢出,而尾数溢出可以通过左移或者右移加上改变阶码的值来达到尾数不溢出的结果。