“科林明伦杯”哈尔滨理工大学第十届程序设计竞赛(同步赛)(A 换根dp B 差分贪心 C 签到 D 条件概率 E 二分 F fib性质 G 网络流 H dp I 思维妙题 J KMP)
题目链接
战绩一般。。
A-点对最大值
思路:换根dp,设dp[u] 为 u子树中某个节点到u 最大权值之和,转移方程:
dp[u]=max(dp[u],dp[v]+w); dp[u]=max(dp[u],c[v]+w);简单换根一下就好了。
#pragma GCC optimize(2)
#include
#define ll long long
#define maxn 1005
#define pb push_back
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
inline ll read()
{
ll x=0,w=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();}
while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();}
return w==1?x:-x;
}
const int N=1e6+10,M=600;
const ll inf=1e15;
int n;
ll c[N];
vectorval[N];
vector >G[N];
ll dp[N],ans;
void dfs(int u,int fa)
{
for(auto now:G[u]){
int v=now.first,w=now.second;
if(v==fa) continue;
dfs(v,u);
//printf("dp[u]:%lld dp[v]+w:%lld c[v]+w:%lld\n",dp[u],dp[v]+w,c[v]+w);
dp[u]=max(dp[u],dp[v]+w);
dp[u]=max(dp[u],c[v]+w);
}
//dp[u]+=c[u];
}
void dfs2(int u,int fa)
{
//printf("u:%d fa:%d dp:%d\n",u,fa,dp[u]);
ans=max(ans,dp[u]+c[u]);
val[u].push_back(-inf);
for(int i=0;i=0;--i){
auto now=G[u][i];
int v=now.first;
ll w=now.second;
if(v==fa) continue;
ll t=dp[u],t1=dp[v];
dp[u]=max(mx,val[u][i]);
dp[v]=max(dp[v],dp[u]+w);
dp[v]=max(dp[v],c[u]+w);
//printf("u:%d v:%d 断边后:dp[u]:%d dp[v]:%d\n",u,v,dp[u],dp[v]);
if(v!=fa) dfs2(v,u);
mx=max(mx,t1+w);
mx=max(mx,c[v]+w);
//dp[v]=t1;
//dp[u]=t;
}
}
int main()
{
int _=read();while(_--)
{
n=read();
rep(i,1,n){G[i].clear();val[i].clear();dp[i]=-inf;}
rep(i,2,n){
int v=read(),w=read();
G[i].push_back(make_pair(v,w));
G[v].push_back(make_pair(i,w));
}
rep(i,1,n) c[i]=read();
dfs(1,-1);
//rep(i,1,n) printf("i:%d dp:%d\n",i,dp[i]);
ans=-inf;
dfs2(1,-1);
printf("%lld\n",ans);
}
}
/*
1
7
1 1
1 -1
2 2
2 -2
3 3
3 3
1 2 3 4 5 6 7
1
4
1 -2
1 -2
1 -3
-2 -2 -3 -4
*/
B-减成一
思路:上场得中北赛出过一摸一样的题,就是要求差分为0就可以了。
答案就是
di为差分值为正,-di 差分值为负
#pragma GCC optimize(2)
#include
#define ll long long
#define maxn 1005
#define inf 1e9
#define pb push_back
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
inline ll read()
{
ll x=0,w=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();}
while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();}
return w==1?x:-x;
}
const int N=1e5+10;
int a[N],n,s[N];
int main()
{
int _=read();while(_--)
{
n=read();
a[0]=1;
rep(i,1,n){
a[i]=read();
}
ll ma1 = 0,ma2 = 0;
for(int i=1;i<=n;++i)
{
ll tmp = a[i]-a[i-1];
if(tmp > 0) ma1 += tmp;
else ma2 -= tmp;
//printf("ma1:%lld ma2:%lld tmp:%lld\n",ma1,ma2,tmp);
}
ll ans = max(ma1,ma2);
printf("%lld\n",ans);
}
}
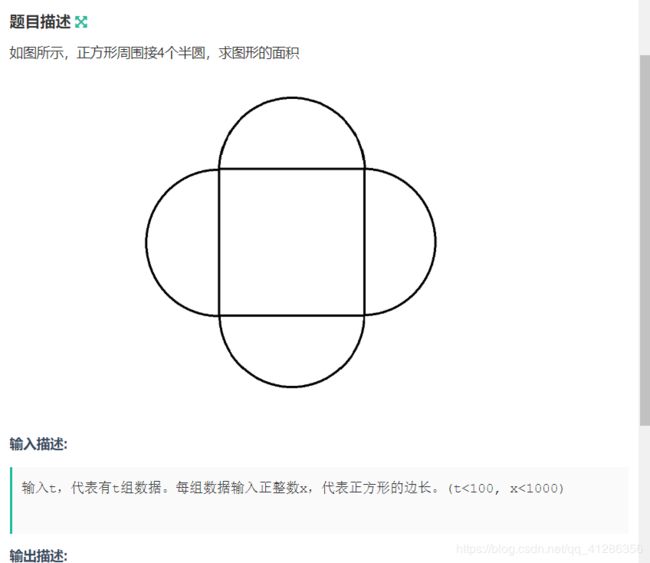
C-面积
签到题
#pragma GCC optimize(2)
#include
#define ll long long
#define maxn 1005
#define inf 1e9
#define pb push_back
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
inline ll read()
{
ll x=0,w=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();}
while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();}
return w==1?x:-x;
}
const int N=1e5+10;
const double pi=3.14;
int a[N],n,s[N];
int main()
{
int _=read();while(_--)
{
double n;
cin>>n;
double r=n/2;
double ans=n*n+pi*r*r*2;
printf("%.2f\n",ans);
}
}
D-扔硬币
做法:条件概率公式
P(B)就是至少有m枚硬币是反面的概率,P(AB)就是恰好有k枚硬币且至少有m枚硬币是反面的概率。水题。
预处理逆元,阶乘的逆元就好了
#pragma GCC optimize(2)
#include
#define maxn 1005
#define inf 1e9
#define pb push_back
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
inline ll read()
{
ll x=0,w=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();}
while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();}
return w==1?x:-x;
}
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
ll powmod(ll a,ll b) {ll res=1;a%=mod;
assert(b>=0); for(;b;b>>=1){if(b&1)res=res*a%mod;a=a*a%mod;}return res;}
const int N=1e5+10;
ll inv[N],f[N],f2[N],inv2[N];
void init()
{
f[0]=1;inv[0]=inv[1]=1;
f2[0]=1;
inv2[0]=1;
for(int i=1;in) return 0;
ll ans=f[n]*inv[m]%mod*inv[n-m]%mod;
return f[n]*inv[m]%mod*inv[n-m]%mod;
}
void add(ll &x,ll y)
{
x=(x+y)%mod;
}
int main()
{
init();
int _=read();while(_--)
{
ll n=read(),m=read(),k=read();
if(n-mn){puts("0");continue;}
ll PB=0;
for(ll i=m;i<=n;++i){
add(PB,C(n,i)*inv2[n]%mod);
//printf("n:%lld i:%lld C:%lld\n",n,i,C(n,i)*inv2[n]%mod);
}
ll PAB=C(n,k)*inv2[n]%mod;
//printf("PB:%lld PB:%lld\n",PAB,PB);
ll ans=PAB*powmod(PB,mod-2)%mod;
printf("%lld\n",ans);
}
}
/*
100
100000 1000 999
*/
E-赛马
做法:这种题不是原题 ,出烂的原题了吗。二分就可以了。
#pragma GCC optimize(2)
#include
#define ll long long
#define maxn 1005
#define inf 1e9
#define pb push_back
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
inline ll read()
{
ll x=0,w=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();}
while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();}
return w==1?x:-x;
}
const int N=1e3+10;
int a[N],n;
multisetst;
int main()
{
int _=read();while(_--)
{
st.clear();
n=read();
rep(i,1,n) a[i]=read();
rep(i,1,n)
{
int x=read();
st.insert(x);
}
int ans=0;
rep(i,1,n)
{
auto it=st.lower_bound(a[i]);
if(it!=st.begin()){
--it;
ans++;
st.erase(it);
}
}
printf("%d\n",ans);
}
}
F-三角形
做法:任意两边之和等于第三边就可以分成最多的段,1 1 2 3 5 这就是简单的fib 数列了。预处理求fib的前缀和,二分一下就可以了。
#pragma GCC optimize(2)
#include
#define maxn 1005
#define inf 1e9
#define pb push_back
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
typedef __int128 ll;
inline ll read()
{
ll x=0,w=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();}
while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();}
return w==1?x:-x;
}
const int N=1e3+10;
const ll M=(1ll<<64)-1;
ll f[N],sum[N];
int len;
int main()
{
f[0]=1,f[1]=1;
f[2]=1;
len=100;
sum[1]=1;sum[2]=2;
for(int i=3;i<=len;++i){
//printf("%lld M:%lld\n",f[i-1]+f[i-2],M);
f[i]=f[i-1]+f[i-2];
sum[i]=sum[i-1]+f[i];
}
//printf("len:%d\n",len);
int _=read();while(_--)
{
ll n=read();
__int128 x=n;
int id=upper_bound(sum+1,sum+1+len,x)-sum;
printf("%d\n",id-1);
}
}
G-养花
做法:补题。
官方题解:
有点没看懂,由于n只有1e4,可以考虑暴力建图。
1、对于每个数拆成两个点,左端点指向右端点,权值为1
2、超级源点S指向h[i]数组,边权为1
3、汇点就是k (2*k)
跑dinic网络流即可
// copy from kuangbin
#include
using namespace std;
using ll = long long;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int INF=0x3f3f3f3f;
const int MAXN=10050;//点数的最大值
const int MAXM=200500;//边数的最大值
struct Node
{
int from,to,next;
int cap;
}edge[MAXM];
int tol;
int dep[MAXN];//dep为点的层次
int head[MAXN];
void init()
{
tol=0;
memset(head,-1,sizeof(head));
}
void addedge(int u,int v,int w)//第一条变下标必须为偶数
{
edge[tol]={u,v,head[u],w};
head[u]=tol++;
edge[tol]={v,u,head[v],0};
head[v]=tol++;
}
int BFS(int start,int end)
{
int que[MAXN];
int front,rear;
front=rear=0;
memset(dep,-1,sizeof(dep));
que[rear++]=start;
dep[start]=0;
while(front!=rear)
{
int u=que[front++];
if(front==MAXN)front=0;
for(int i=head[u];i!=-1;i=edge[i].next)
{
int v=edge[i].to;
if(edge[i].cap>0&&dep[v]==-1)
{
dep[v]=dep[u]+1;
que[rear++]=v;
if(rear>=MAXN)rear=0;
if(v==end)return 1;
}
}
}
return 0;
}
int dinic(int start,int end)
{
int res=0;
int top;
int stack[MAXN];//stack为栈,存储当前增广路
int cur[MAXN];//存储当前点的后继
while(BFS(start,end))
{
memcpy(cur,head,sizeof(head));
int u=start;
top=0;
while(1)
{
if(u==end)
{
int min=INF;
int loc;
for(int i=0;iedge[stack[i]].cap)
{
min=edge[stack[i]].cap;
loc=i;
}
for(int i=0;i
H-直线
题目都很简洁呀
做法:设dp[i]为当前i条线最大的交点,每新增一条线的最大贡献就是跟前面的线全部有一次交点。dp[i]=dp[i-1]+i-1
#pragma GCC optimize(2)
#include
#define ll long long
#define maxn 1005
#define inf 1e9
#define pb push_back
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
inline ll read()
{
ll x=0,w=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();}
while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();}
return w==1?x:-x;
}
const int N=1e5+10;
const double pi=3.14;
int a[N],n,s[N];
void print(__int128 x)
{
stacksta;
while(x)
{
sta.push(x%10);
x=x/10;
}
while(sta.size()) printf("%d",sta.top()),sta.pop();
puts("");
}
int main()
{
int _=read();while(_--)
{
ll n=read();
if(n==1){
puts("0");
continue;
}
__int128 t=n-1;
__int128 ans=t*(t+1)/2;
print(ans);
}
}
I-字典序
补题。。
做法:来自官方题解
想到了思路,但是不知道怎么处理,建了图跑拓扑然后wa,这里怎么处理呢,对去掉连续相同的数,从后往前遍历,用deque维护一下就可以了。很妙的做法。
//deque妙用
#pragma GCC optimize(2)
#include
#define ll long long
#define maxn 1005
#define inf 1e9
#define pb push_back
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
inline ll read()
{
ll x=0,w=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();}
while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();}
return w==1?x:-x;
}
const int N=1e5+10;
int a[N],n,b[N],l[N],r[N],len;
int main()
{
int _=read();while(_--)
{
n=read();len=0;
dequeque;
rep(i,1,n) {a[i]=read();}
for(int i=1;i<=n;++i){
int j=i;
while(j+1<=n&&a[j+1]==a[j]) ++j;
b[++len]=a[i];
l[len]=i,r[len]=j;
i=j;
}
que.push_front(len);
for(int i=len-1;i>=1;--i){
if(b[i]>b[i+1]) que.push_front(i);
else que.push_back(i);
}
for(auto v:que){
for(int i=l[v];i<=r[v];++i) printf("%d ",i);
}
puts("");
}
}
/*
100
4
2 3 2 1
ans: 2 3 4 1
6
2 2 3 3 2 1
ans: 3 4 5 6 1 2
6
2 2 3 3 2 100
*/
J-最大值
做法:这题描述的不就kmp 的next数组的性质吗?判断next数组中最大值就可以了。
#pragma GCC optimize(2)
#include
#define ll long long
#define maxn 1005
#define inf 1e9
#define pb push_back
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
inline ll read()
{
ll x=0,w=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();}
while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();}
return w==1?x:-x;
}
const int N=1e5+10;
int ne[N],len;
char b[N];
void get() //常规处理方法
{
ne[0]=-1;
for(int i=0,j=-1;i