Poisson方程五点差分格式例题及解答
- 写在前面
- 例题
- 解题过程
- 总结
- 参考
写在前面
本文针对偏微分方程数值解中出现的一道例题进行分析,详细介绍了五点差分格式的公式推导及应用。
例题
在单位正方形 Ω ‾ : 0 ⩽ x ⩽ 1 , 0 ⩽ y ⩽ 1 \overline{\Omega}:\,0\leqslant x\leqslant1,\,\,0\leqslant y\leqslant1 Ω:0⩽x⩽1,0⩽y⩽1上,
{ Δ u = − 16 , ( x , y ) ∈ Ω u ∣ x = 1 = 0 , ∂ u ∂ y ∣ y = 1 = − u ∂ u ∂ x ∣ x = 0 = ∂ u ∂ y ∣ y = 0 = 0 \left\{\begin{aligned} &\Delta u=-16,\quad (x, y)\in\Omega\\ &u|_{x=1}=0,\quad \frac{\partial u}{\partial y}|_{y=1}=-u\\ & \frac{\partial u}{\partial x}|_{x=0}=\frac{\partial u}{\partial y}|_{y=0}=0\\ \end{aligned}\right. ⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧Δu=−16,(x,y)∈Ωu∣x=1=0,∂y∂u∣y=1=−u∂x∂u∣x=0=∂y∂u∣y=0=0
在 Ω ‾ \overline{\Omega} Ω上布置以 h = 1 4 h=\frac14 h=41为步长的正方形网格,写出五点差分格式解上述问题的方程组。
解题过程
由于其步长为 h = 1 4 h=\frac14 h=41,再根据边值条件,可知
x = 1 x=1 x=1这条轴上的五个点其值均为 0 0 0,故可得图如下,一共有20个未知量,其中有9个正则内点和11个边界点。
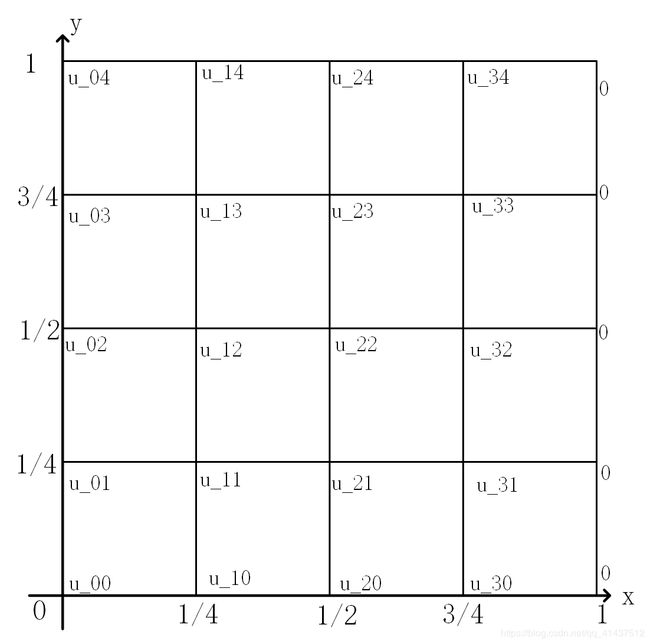
首先计算内点:
对于9个正则内点 u i , j , i = 1 , 2 , 3 ; j = 1 , 2 , 3 u_{i,j},i=1,2,3;j=1,2,3 ui,j,i=1,2,3;j=1,2,3,由五点差分格式公式可以得到:
u i + 1 , j + u i , j + 1 + u i , j − 1 + u i − 1 , j − 4 u i , j = − 16 × 1 4 2 = − 1 u_{i+1,j}+u_{i,j+1}+u_{i,j-1}+u_{i-1,j}-4u_{i,j}=-16\times\frac{1}{4^2}=-1 ui+1,j+ui,j+1+ui,j−1+ui−1,j−4ui,j=−16×421=−1
即:
4 u i , j − ( u i + 1 , j + u i , j + 1 + u i , j − 1 + u i − 1 , j ) = 1 , i , j = 1 , 2 , 3 (1) 4u_{i,j}-(u_{i+1,j}+u_{i,j+1}+u_{i,j-1}+u_{i-1,j})=1,\quad i,j=1,2,3 \tag{1} 4ui,j−(ui+1,j+ui,j+1+ui,j−1+ui−1,j)=1,i,j=1,2,3(1)
再计算边界点:
①对于下边界 ∂ u ∂ y ∣ y = 0 = 0 \left.\frac{\partial u}{\partial y}\right|_{y=0}=0 ∂y∂u∣∣∣y=0=0,用一阶中心差商代替一阶偏导数,得到
u i , 1 − u i , − 1 2 h = 0 , \frac{u_{i,1}-u_{i,-1}}{2h}=0, 2hui,1−ui,−1=0,
即 u i , 1 = u i , − 1 u_{i,1}=u_{i,-1} ui,1=ui,−1,又因为 j = 0 j=0 j=0时,
4 u i , 0 − ( u i + 1 , 0 + u i , 1 + u i , − 1 + u i − 1 , 0 ) = 1 , 4u_{i,0}-(u_{i+1,0}+u_{i,1}+u_{i,-1}+u_{i-1,0})=1, 4ui,0−(ui+1,0+ui,1+ui,−1+ui−1,0)=1,
代入 u i , 1 = u i , − 1 u_{i,1}=u_{i,-1} ui,1=ui,−1得到
2 u i , 0 − ( 1 2 u i + 1 , 0 + u i , 1 + 1 2 u i − 1 , 0 ) = 1 2 , i = 1 , 2 , 3 (2) 2u_{i,0}-\left(\frac12 u_{i+1,0}+u_{i,1}+\frac12 u_{i-1,0}\right)=\frac{1}{2},\quad i=1,2,3\tag{2} 2ui,0−(21ui+1,0+ui,1+21ui−1,0)=21,i=1,2,3(2)
②对左边界 ∂ u ∂ x ∣ x = 0 = 0 \left.\frac{\partial u}{\partial x}\right|_{x=0}=0 ∂x∂u∣∣x=0=0,同理得到:
2 u 0 , j − ( 1 2 u 0 , j + 1 + u 1 , j + 1 2 u 0 , j − 1 ) = 1 2 , j = 1 , 2 , 3 (3) 2u_{0,j}-\left(\frac12 u_{0,j+1}+u_{1,j}+\frac12 u_{0,j-1}\right)=\frac{1}{2},\quad j=1,2,3\tag{3} 2u0,j−(21u0,j+1+u1,j+21u0,j−1)=21,j=1,2,3(3)
③对上边界 ∂ u ∂ y ∣ y = 1 = − u \left.\frac{\partial u}{\partial y}\right|_{y=1}=-u ∂y∂u∣∣∣y=1=−u,用一阶中心差商代替一阶偏导数,得到 u i , 5 = u i , 3 − 1 2 u i , 4 u_{i,5}=u_{i,3}-\frac12 u_{i,4} ui,5=ui,3−21ui,4,所以得到:
9 4 u i , 4 − ( 1 2 u i + 1 , 4 + u i , 3 + 1 2 u i − 1 , 4 ) = 1 2 , i = 1 , 2 , 3 (4) \frac94 u_{i,4}-\left(\frac12 u_{i+1,4}+u_{i,3}+\frac12 u_{i-1,4}\right)=\frac{1}{2},\quad i=1,2,3\tag{4} 49ui,4−(21ui+1,4+ui,3+21ui−1,4)=21,i=1,2,3(4)
④对点 u 0 , 0 = ( 0 , 0 ) u_{0,0}=(0,0) u0,0=(0,0),根据下边界和左边界的式子,可以分别得到:
2 u 0 , 0 − ( 1 2 u 1 , 0 + u 0 , 1 + 1 2 u − 1 , 0 ) = 1 2 , 2u_{0,0}-\left(\frac12 u_{1,0}+u_{0,1}+\frac12 u_{-1,0}\right)=\frac{1}{2}, 2u0,0−(21u1,0+u0,1+21u−1,0)=21,
2 u 0 , 0 − ( 1 2 u 0 , 1 + u 1 , 0 + 1 2 u 0 , − 1 ) = 1 2 , 2u_{0,0}-\left(\frac12 u_{0,1}+u_{1,0}+\frac12 u_{0,-1}\right)=\frac{1}{2}, 2u0,0−(21u0,1+u1,0+21u0,−1)=21,
以及内点差分方程 ( 1 ) (1) (1)式
4 u 0 , 0 − ( u 1 , 0 + u 0 , 1 + u 0 , − 1 + u − 1 , 0 ) = 1 4u_{0,0}-\left(u_{1,0}+u_{0,1}+u_{0,-1}+u_{-1,0}\right)=1 4u0,0−(u1,0+u0,1+u0,−1+u−1,0)=1
可得:
u 0 , 0 − 1 2 u 1 , 0 − 1 2 u 0 , 1 = 1 4 . u_{0,0}-\frac{1}{2}u_{1,0}-\frac{1}{2}u_{0,1}=\frac14. u0,0−21u1,0−21u0,1=41.
⑤对点 u 0 , 4 u_{0,4} u0,4,同理可由左边界和上边界的式子分别得到:
2 u 0 , 4 − ( 1 2 u 0 , 5 + u 1 , 4 + 1 2 u 0 , 3 ) = 1 2 , 2u_{0,4}-\left(\frac12 u_{0,5}+u_{1,4}+\frac12 u_{0,3}\right)=\frac{1}{2}, 2u0,4−(21u0,5+u1,4+21u0,3)=21,
9 4 u 0 , 4 − ( 1 2 u 1 , 4 + u 0 , 3 + 1 2 u − 1 , 4 ) = 1 2 , \frac94 u_{0,4}-\left(\frac12 u_{1,4}+u_{0,3}+\frac12 u_{-1,4}\right)=\frac{1}{2}, 49u0,4−(21u1,4+u0,3+21u−1,4)=21,
以及内点差分方程 ( 1 ) (1) (1)式
4 u 0 , 4 − ( u 1 , 4 + u 0 , 5 + u 0 , 3 + u − 1 , 4 ) = 1. 4u_{0,4}-\left(u_{1,4}+u_{0,5}+u_{0,3}+u_{-1,4}\right)=1. 4u0,4−(u1,4+u0,5+u0,3+u−1,4)=1.
可得:
9 8 u 0 , 4 − 1 2 u 1 , 4 − 1 2 u 0 , 3 = 1 4 . \frac98u_{0,4}-\frac{1}{2}u_{1,4}-\frac{1}{2}u_{0,3}=\frac14. 89u0,4−21u1,4−21u0,3=41.
总结
在运用五点差分格式时,要把握好对初值及边值条件的求解,其步骤一般为:
- 作草图,找正则内点和边界点;
- 代入五点差分格式公式,得到正则内点表达式;
- 分别根据边值及初值条件计算边界上的点和角位置的点;
- 如果需要,可将方程组转化为矩阵形式。
在进行计算时,还可以整理成矩阵的形式,便于计算机求解。
参考
[1] 常微分数值方法部分课后习题答案