19聚类算法-Kmeans ;20聚类算法-DBSCAN;21案例实战:聚类实践
唐宇迪《python数据分析与机器学习实战》学习笔记
19聚类算法-Kmeans;20聚类算法-DBSCAN;21案例实战:聚类实践
一、K-Means算法
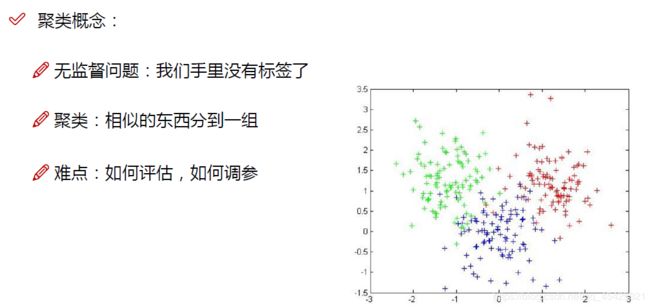
右边图原始数据集上没有标色,这里把类型相似的分在一块形成了3团簇。
1.K-Means算法基本概念
最简单也是最实用的算法

大多时候使用欧式距离,加入X轴为(0.01、0.04、0.03) y轴为(105、161、261)那么X轴无论怎么算数据之间的差异性都很小,Y轴差异大,潜意思认为Y轴决定相似度了,因此基本所有情况下要进行标准化,例如归一化,让XY轴的范围都是(0-1)。
优化:让簇里面所有样本点到中心点的距离的和最小,越小代表越相似。
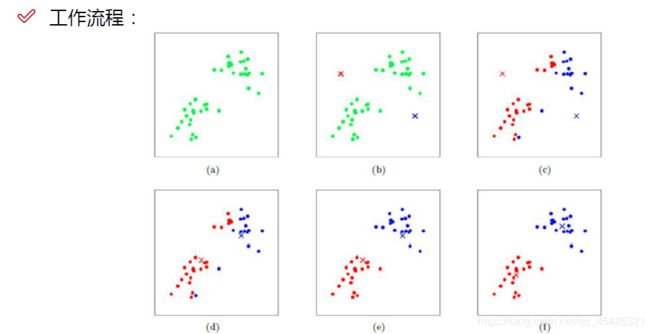
2. 工作流程
(a)无监督问题,最开始不知道点属于那些簇;(b)例如k=2就随机初始化2个点,算其他点到这两个点的距离
(c)大量迭代后,根据距离划分为两堆;(d)所以更新衡量依据,更新质心,根据所有点算出他们的新质心;
(e)更新后重新计算,遍历所有点到新质心距离,重新划分,重新再计算质心。(f)再遍历计算。。。
多次循环指导不再变化了
然后登陆网址:https://www.naftaliharris.com/blog/visualizing-k-means-clustering/,看一下这个算法的可视化展示
便于理解这个算法。

3.进行图像压缩小例子
from skimage import io
from sklearn.cluster import KMeans
import numpy as np
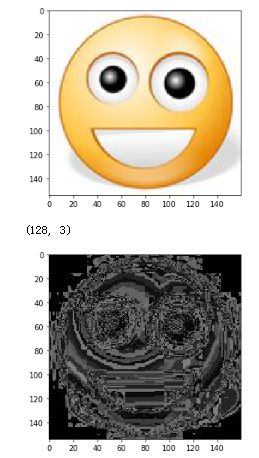
image = io.imread('test2.jpg')
io.imshow(image)
io.show()
# print(image.shape) #(154, 160, 3) 每个点由3个元素组成
rows = image.shape[0] #行列输出看一下有多少个像素点
cols = image.shape[1]
#原来图像是一个彩色图,h*w*c,有一个通道C,现在换成 样本*c
image = image.reshape(image.shape[0]*image.shape[1],3)
kmeans = KMeans(n_clusters = 128, n_init=10, max_iter=200)
#把集合分为个簇
kmeans.fit(image)
clusters = np.asarray(kmeans.cluster_centers_,dtype=np.uint8) #点标签
labels = np.asarray(kmeans.labels_,dtype=np.uint8 )
labels = labels.reshape(rows,cols); #为了组成图像又reshape回去
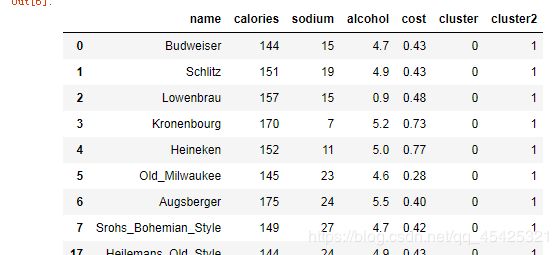
print (clusters.shape)
np.save('codebook_test.npy',clusters)
io.imsave('compressed_test.jpg',labels)
image = io.imread("compressed_test.jpg")
io.imshow(image)
io.show()
二、DBSCAN算法
k-means有些缺点,而DBSCAN非常强大,基于密度带有噪声点,表达效果很强
2.1基本概念

以一个点为圆心划圆,如果这个圈里面的样本数量>阀值,就认为其为核心点。圈的半径和阀值需要我们自己指定。最终多少堆,算法自己求出来。直接密度可达互相传播导致了密度可达。

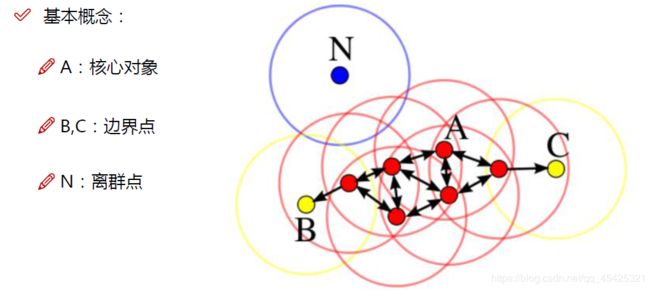
有了离群点,就可以用于异常检测。
2.2工作流程

随便选择一个点画圈,不停“发展下线”,直到已经圈不到了,就形成了一个簇。然后还没标记的里面再重复操作。


然后登陆网址:https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/,看一下这个算法的可视化展示
便于理解这个算法。

epsilon:半径,minPoints:阀值,这里可以在网站上进行调节。
三、案例实战:聚类实践
根据数据对比看一下各类聚类算法

接下来进行实例操作
导入一个啤酒的数据:
# beer dataset
import pandas as pd
beer = pd.read_csv('data.txt', sep=' ')
beer
3.1K_means处理
X = beer[["calories","sodium","alcohol","cost"]] #选出要用的数据
from sklearn.cluster import KMeans #导入算法模块
km = KMeans(n_clusters=3).fit(X) #聚成3堆,传入X训练
km2 = KMeans(n_clusters=2).fit(X)
km.labels_ #查看分类结果
array([0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 2, 0, 0, 2, 1])
#把两次分类结果导入原来数据并排序看看
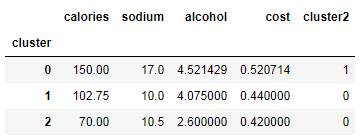
beer['cluster'] = km.labels_
beer['cluster2'] = km2.labels_
beer.sort_values('cluster')
from pandas.plotting import scatter_matrix
%matplotlib inline
cluster_centers = km.cluster_centers_
cluster_centers_2 = km2.cluster_centers_
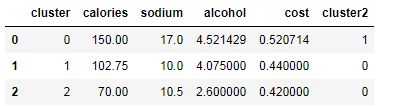
beer.groupby("cluster").mean() #查看一下三堆的中心点坐标
beer.groupby("cluster2").mean()
centers = beer.groupby("cluster").mean().reset_index()#中心点拿出来绘图
centers
%matplotlib inline
import matplotlib.pyplot as plt #绘图模块导入
plt.rcParams['font.size'] = 14
import numpy as np
colors = np.array(['red', 'green', 'blue', 'yellow']) #传入颜色
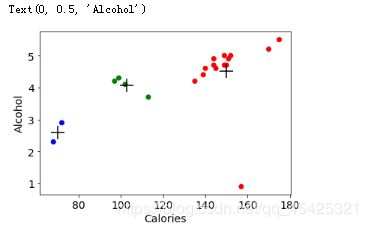
plt.scatter(beer["calories"], beer["alcohol"],c=colors[beer["cluster"]]) #以酒精度、卡路里绘数据点
plt.scatter(centers.calories, centers.alcohol, linewidths=3, marker='+', s=300, c='black')#绘中心点
plt.xlabel("Calories")
plt.ylabel("Alcohol")
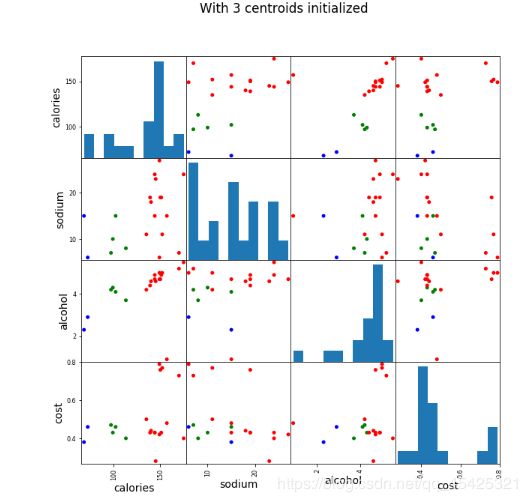
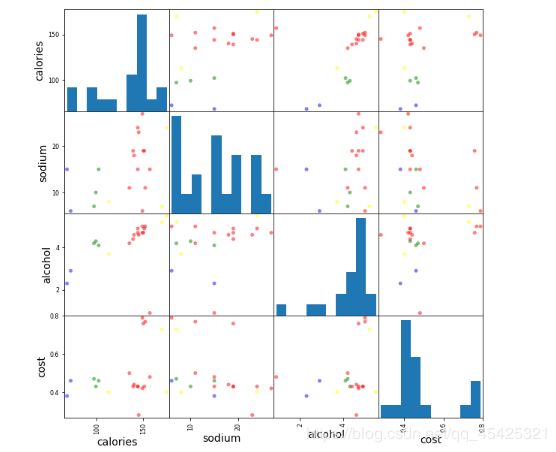
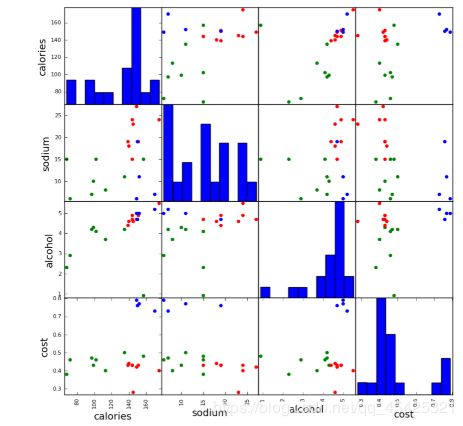
#四个维度两两对应看一下(这里先看分类为3簇的结果)
scatter_matrix(beer[["calories","sodium","alcohol","cost"]],s=100, alpha=1, c=colors[beer["cluster"]], figsize=(10,10))
plt.suptitle("With 3 centroids initialized")
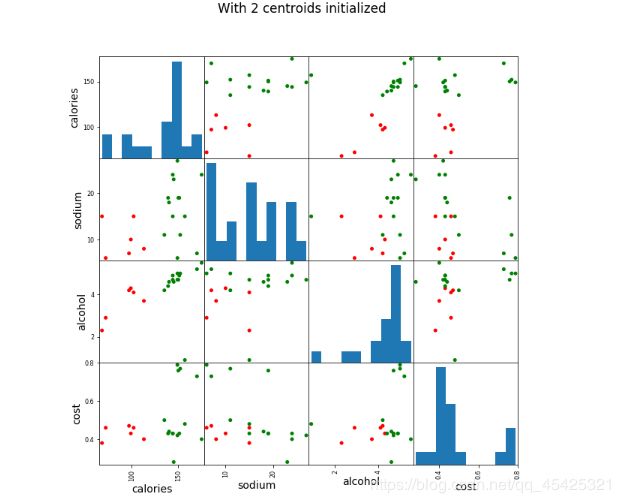
(分类为两簇的结果展示)
scatter_matrix(beer[["calories","sodium","alcohol","cost"]],s=100, alpha=1, c=colors[beer["cluster2"]], figsize=(10,10))
plt.suptitle("With 2 centroids initialized")
from sklearn.preprocessing import StandardScaler #数据归一化模块
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
X_scaled
array([[ 0.38791334, 0.00779468, 0.43380786, -0.45682969],
[ 0.6250656 , 0.63136906, 0.62241997, -0.45682969],
[ 0.82833896, 0.00779468, -3.14982226, -0.10269815],
[ 1.26876459, -1.23935408, 0.90533814, 1.66795955],
[ 0.65894449, -0.6157797 , 0.71672602, 1.95126478],
[ 0.42179223, 1.25494344, 0.3395018 , -1.5192243 ],
[ 1.43815906, 1.41083704, 1.1882563 , -0.66930861],
[ 0.55730781, 1.87851782, 0.43380786, -0.52765599],
[-1.1366369 , -0.7716733 , 0.05658363, -0.45682969],
[-0.66233238, -1.08346049, -0.5092527 , -0.66930861],
[ 0.25239776, 0.47547547, 0.3395018 , -0.38600338],
[-1.03500022, 0.00779468, -0.13202848, -0.24435076],
[ 0.08300329, -0.6157797 , -0.03772242, 0.03895447],
[ 0.59118671, 0.63136906, 0.43380786, 1.88043848],
[ 0.55730781, -1.39524768, 0.71672602, 2.0929174 ],
[-2.18688263, 0.00779468, -1.82953748, -0.81096123],
[ 0.21851887, 0.63136906, 0.15088969, -0.45682969],
[ 0.38791334, 1.41083704, 0.62241997, -0.45682969],
[-2.05136705, -1.39524768, -1.26370115, -0.24435076],
[-1.20439469, -1.23935408, -0.03772242, -0.17352445]])
#用新数据分类,并给原数据传入新的一列
km = KMeans(n_clusters=3).fit(X_scaled)
beer["scaled_cluster"] = km.labels_
beer.sort_values("scaled_cluster")
beer.groupby("scaled_cluster").mean()
pd.scatter_matrix(X, c=colors[beer.scaled_cluster], alpha=1, figsize=(10,10), s=100)
聚类评估:轮廓系数

-计算样本i到同簇其他样本的平均距离ai。ai 越小,说明样本i越应该被聚类到该簇。将ai 称为样本i的簇内不相似度。
-计算样本i到其他某簇Cj 的所有样本的平均距离bij,称为样本i与簇Cj 的不相似度。定义为样本i的簇间不相似度:bi =min{bi1, bi2, …, bik} b(i)越大越好,a(i)越小越好
- si接近1,则说明样本i聚类合理
- si接近-1,则说明样本i更应该分类到另外的簇
- 若si 近似为0,则说明样本i在两个簇的边界上。
from sklearn import metrics#轮廓系数得分值
score_scaled = metrics.silhouette_score(X,beer.scaled_cluster) #归一化结果
score = metrics.silhouette_score(X,beer.cluster) #没有归一化的结果
print(score_scaled, score)
0.1797806808940007 0.6731775046455796
发现不做归一化反而结果比较好,证明因素权重更接近未归一化时
for k in range(2,20): #K值(分几堆好)选择,遍历看K为何值时轮廓系数最大
labels = KMeans(n_clusters=k).fit(X).labels_
score = metrics.silhouette_score(X, labels)
scores.append(score)
scores
[0.6917656034079486,
0.6731775046455796,
0.5857040721127795,
0.4355716067265819,
0.3879716094433995,
0.43776116697963124,
0.38946337473125997,
0.39746405172426014,
0.4081599013899603,
0.32472080133848924,
0.3459775237127248,
0.31221439248428434,
0.30707782144770296,
0.31834561839139497,
0.2849514001174898,
0.23498077333071996,
0.1588091017496281,
0.08423051380151177]
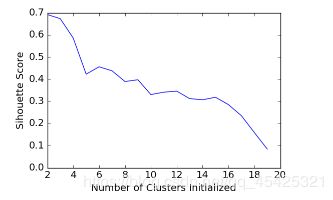
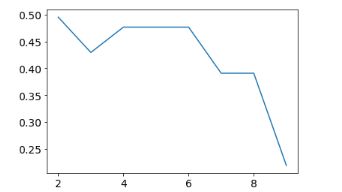
#将每个K对应的轮廓系数值画折线图看看
plt.plot(list(range(2,20)), scores)
plt.xlabel("Number of Clusters Initialized")
plt.ylabel("Sihouette Score")
3.2DBSCAN处理
#导入DBSCAN模块训练,取出标签展示
from sklearn.cluster import DBSCAN
db = DBSCAN(eps=10, min_samples=2).fit(X) #指定圈半径以及圈内最小样本数
labels = db.labels_
beer['cluster_db'] = labels
beer.sort_values('cluster_db')
beer.groupby('cluster_db').mean()
scatter_matrix(X, c=colors[beer.cluster_db], figsize=(10,10), s=100)
score_as =[]
for k in range(2,10):
labels =DBSCAN(eps=10,min_samples=k).fit(X).labels_
score_a = metrics.silhouette_score(X, labels)
score_as.append(score_a)
plt.plot(list(range(2,10)), score_as)
看一下半径对结果的影响(注意这里半径太大会报错,因为全部都分为一类了)
score_bs =[]
for k in range(10,26):
labels =DBSCAN(eps=k,min_samples=2).fit(X).labels_
score_b = metrics.silhouette_score(X, labels)
score_bs.append(score_b)
plt.plot(list(range(10,26)), score_bs)