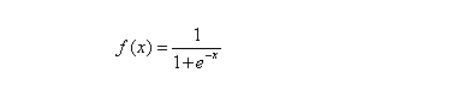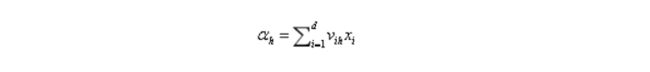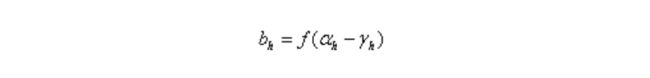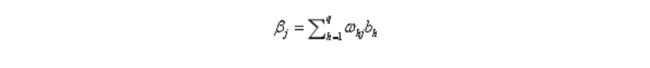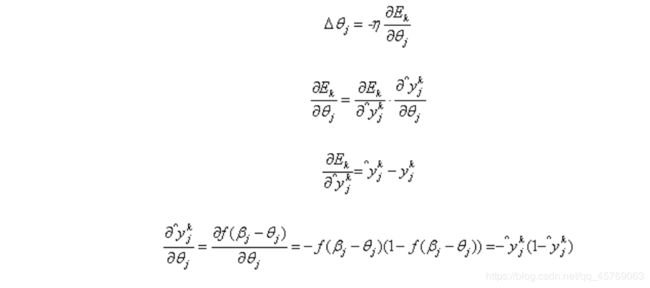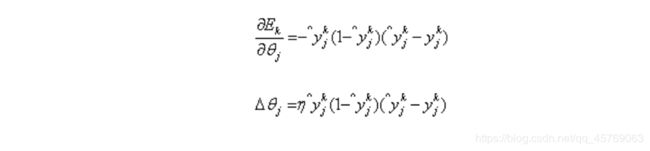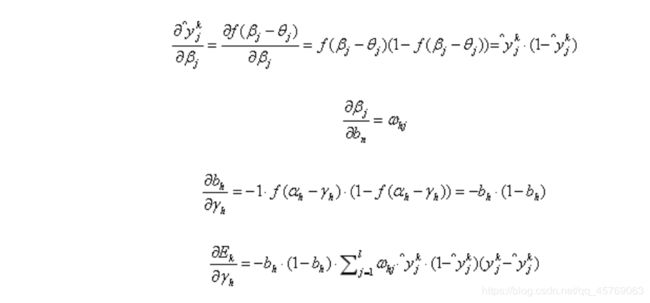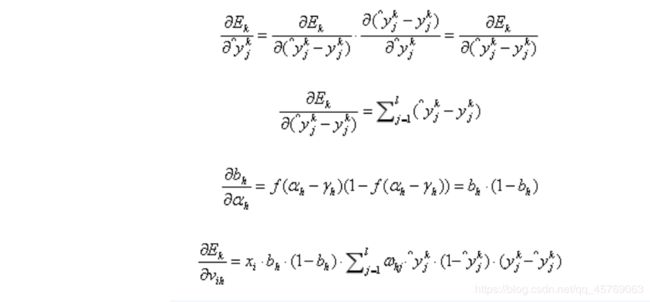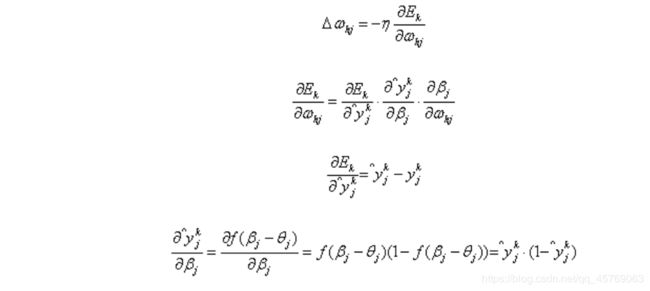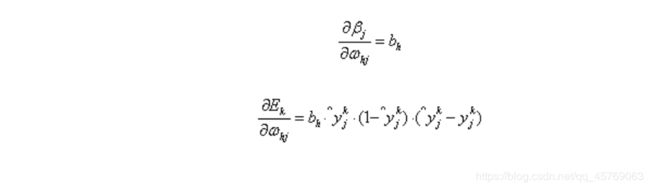机器学习——人工神经网络之BP算法编程(python二分类数据集:马疝病数据集)
目录
一、理论知识回顾
1、神经网络模型
2、明确任务以及参数
1)待估参数:
2)超参数:
3)任务
3、神经网络数学模型定义
1)激活函数
2)各层权重、阈值定义
3)各层输入输出定义
4、优化问题的目标函数与迭代公式
1)目标函数
2)待估参数的优化迭代公式
二、python编程
1、编程步骤
2、数据准备、数据处理、数据划分
1)数据下载
2)关键代码
3、初始化待估参数
1)关键代码
2)np.random.randint(a,b,(m,n))函数
3)astype(np.float64)
4、创建激活函数
5、参数迭代更新
1)关键代码
2)dot、multiply
3)难点
6、测试模型
7、主函数运行
三、总结
1、几个循环
2、问题集锦
1)若是有多个输出怎么办?
2)BP算法为什么叫做后向传播?
四、完整代码
坚持嗑完这篇文章一定会明白神经网络BP算法的精髓所在的,以及各层之间误差的互相影响以及传播
一、理论知识回顾
参考文章:
《机器学习——人工神经网络之发展历史(神经元数学模型、感知器算法)》
《机器学习——人工神经网络之多层神经网络(多层与三层)》
《机器学习——人工神经网络之后向传播算法(BP算法)》
《机器学习——人工神经网络之参数设置(BP算法)》
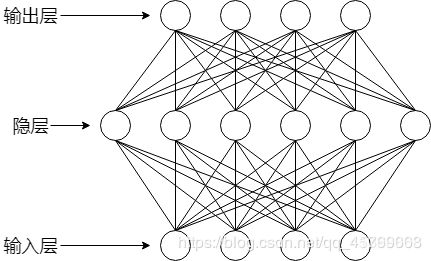
1、神经网络模型
一个神经元即一个感知机模型,由多个神经元相互连接形成的网络,即神经网络。
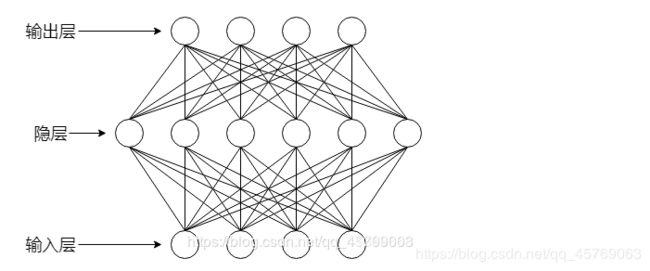
这里我们只讨论单隐层前馈神经网络,其连接形式入下:
2、明确任务以及参数
1)待估参数:
每个神经元的阈值b或者value,以及神经元之间的连接权重weight。
2)超参数:
超参数就是求解不出来,需要用户自己定义的参数,如在神经网络中,超参数有:
神经网络隐层的层数,一般只考虑隐层的层数,因为输入层和输出层一般默认为一层
每一层神经网络的神经元个数:神经元的个数直接影响着待估参数的个数,假设隐层第m层有k个神经元,第m+1层有l个神经元,那么这两层之间的权重系数weight的个数为k*l个,一般组成(k,l)矩阵的形式;每一层的阈值或者叫做偏置的个数和神经元个数相同
神经网络:可能这个听起来比较抽象,但是这就是需要自己进行定义的,具体见代码,主要是指定神经网络层数,每层神经元的个数,确定待估参数的初始值就基本上将神经网络给定义好了
3)任务
通过训练样本将定义的神经网络模型进行不断的优化,将待测参数进行不断的迭代,直到满足条件为止(条件理论上是目标函数E对所有的待测参数的偏导为0,但是计算机没有绝对的0值,因此一般通过迭代次数和偏导的最小值来作为迭代的终止条件)
3、神经网络数学模型定义
对于该模型有如下定义:
训练集:D={(x1, y1), (x2, y2), ......, (xm, ym)},x具有d个属性值,y具有k个可能取值
则我们的神经网络(单隐层前馈神经网络)应该是具有d个输入神经元,q个隐层神经元,k个输出层神经元的神经网络 ,我们默认输入层只是数据的输入,不对数据做处理,即输入层没有阈值。
1)激活函数
2)各层权重、阈值定义
输出层第j个神经元的阈值为:θj
隐层第h个神经元的阈值为:γh(γ是Gamma)
输入层第i个神经元与隐层第h个神经元的连接权重为:vih
隐层第h个神经元与输出层第j个神经元的连接权重为:ωhj
3)各层输入输出定义
输入层的输入和输出一样,就是样本数据
隐层第h个神经元的输入
隐层第h个神经元的输出
输出层第j个神经元的输入
输出层的输出跟隐层的输出类似
4、优化问题的目标函数与迭代公式
1)目标函数
对参数进行估计,需要有优化方向,我们继续使用欧式距离,或者均方误差来作为优化目标:
2)待估参数的优化迭代公式
我们使用梯度下降的策略对参数进行迭代优化,所以任意一个参数的变化大小为(θ代表任意参数):
下面根据这个更新公式,我们来求各个参数的更新公式:
对数几率函数的导数如下:
输出层第j个神经元的阈值θj:
隐层第h个神经元的阈值γh:
输入层第i个神经元与隐层第h个神经元的连接权重vih :
隐层第h个神经元与输出层第j个神经元的连接权重ωhj:
现在四个参数的更新规则都计算出来了,我们可以开始编码实现了。
现在有一个问题:在二分类任务中,输出层神经元有几个?
一个:如果只有1个,那么输出0表示反例,1表示正例
二个:那么输出(1,0)表示反例,(0,1)表示正例
以下实例我们使用第一种:即输出层的神经元只有一个
二、python编程
1、编程步骤
数据准备(通过读取数据文件获取)
数据处理(读取的数据是字符串形式,需要将其转换为浮点数或者整型)
数据划分(将特征和标签分割开)
初始化待估参数(通过自定义超参数每层神经元的个数来进行初始化待估参数)——这里不需要定义层数,因为这里只有一个隐层
参数迭代更新(用初始化的待估参数去对样本数据进行逐一训练,并且不断地迭代更新,最后得到最优的待估参数)——这里和上一步其实就基本上将整个神经网络的框架已经搭建好了
测试模型(利用上面得到的参数,对测试样本集进行测试,查看准确率)
2、数据准备、数据处理、数据划分
1)数据下载
我们使用一个二分类数据集:马疝病数据集
UCI下载地址为:http://archive.ics.uci.edu/ml/datasets/Horse+Colic
或者:
以下是用户《9527----到》提供的,可见文章:《基于tensorflow的logistics回归--数据集为 horseColicTest and horseColicTraining.txt(文章底部附数据集链接)》文末
测试集
https://pan.baidu.com/s/1h1t0LLxZlESPPdfn1zxTXQ
训练集
https://pan.baidu.com/s/1IVO2opIQ0e66_AEchw_X4Q
2)关键代码
#创建加载数据读取数据以及划分数据集的函数,返回数据特征集以及数据标签集
def loaddataset(filename):
fp = open(filename)#(299,22)
# 存放数据
dataset = []
# 存放标签
labelset = []
for i in fp.readlines():#按照行来进行读取,每次读取一行,一行的数据作为一个元素存放在了类别中
a = i.strip().split()#去掉每一行数据的空格以及按照默认的分隔符进行划分
# 每个数据行的最后一个是标签
dataset.append([float(j) for j in a[:len(a) - 1]])#读取每一行中除最后一个元素的前面的元素,并且将其转换为浮点数
labelset.append(int(float(a[-1])))#读取每一行的最后一个数据作为标签数据
return dataset, labelset#dataset是(299,21)的列表,labelset是(299,1)的列表
3、初始化待估参数
1)关键代码
# x为输入层神经元个数,y为隐层神经元个数,z输出层神经元个数
#创建的是参数初始化函数,参数有各层间的权重weight和阈值即偏置value就是b
#本例的x,y=len(dataset[0])=22,z=1
def parameter_initialization(x, y, z):
# 隐层阈值
value1 = np.random.randint(-5, 5, (1, y)).astype(np.float64)#随机生成(-5,5)之间的整数组成(1,y)的数组,然后再将其转为浮点数显示
# 输出层阈值
value2 = np.random.randint(-5, 5, (1, z)).astype(np.float64)
# 输入层与隐层的连接权重
weight1 = np.random.randint(-5, 5, (x, y)).astype(np.float64)
# 隐层与输出层的连接权重
weight2 = np.random.randint(-5, 5, (y, z)).astype(np.float64)
return weight1, weight2, value1, value2
'''
weight1:输入层与隐层的连接权重
weight2:隐层与输出层的连接权重
value1:隐层阈值
value2:输出层阈值
权重和阈值的个数和神经网络的隐层层数有关,若隐层为n,则权重和阈值的个数为n+1
'''2)np.random.randint(a,b,(m,n))函数
np.random.randint(a,b,(m,n))
#在指定的范围内随机生成整数
#a,区间上限,b,区间下限,size=(m,n),aimport numpy as np
a = np.random.randint(-5,5,size=(2,4))
print(a)
print(type(a))
[[-1 3 -5 3]
[-3 1 -4 4]]
3)astype(np.float64)
将元素转化为指定的类型进行显示
import numpy as np
a = np.random.randint(-5,5,size=(2,4)).astype(np.float64)
print(a)
print(type(a))
[[-1. -2. -3. 3.]
[ 3. -2. -2. -3.]]
4、创建激活函数
#创建激活函数sigmoid
def sigmoid(z):
return 1 / (1 + np.exp(-z))
5、参数迭代更新
这里是对所有的样本逐一进行训练一轮的函数,即对整个训练样本进行了一次迭代,若要循环迭代,则需要在外层再套一层循环,来表示迭代的次数,本例将其直接放在了主函数中进行迭代的不断循环
1)关键代码
#创建训练样本的函数,返回训练完成后的参数weight和value,这里的函数是经过一次迭代后的参数,即所有的样本经过一次训练后的参数
#具体参数的值可以通过设置迭代次数和允许误差来进行确定
def trainning(dataset, labelset, weight1, weight2, value1, value2):
# x为步长
x = 0.01#学习率
for i in range(len(dataset)):#依次读取数据特征集中的元素,一个元素即为一个样本所含有的所有特征数据
# 输入数据
#(1,21)
inputset = np.mat(dataset[i]).astype(np.float64)#每次输入一个样本,将样本的特征转化为矩阵,以浮点数显示
# 数据标签
#(1,1)
outputset = np.mat(labelset[i]).astype(np.float64)#输入样本所对应的标签
# 隐层输入,隐层的输入是由输入层的权重决定的,wx
#input1:(1,21).(21,21)=(1,21)
input1 = np.dot(inputset, weight1).astype(np.float64)
# 隐层输出,由隐层的输入和阈值以及激活函数决定的,这里的阈值也可以放在输入进行计算
#sigmoid((1,21)-(1,21))=(1,21)
output2 = sigmoid(input1 - value1).astype(np.float64)
# 输出层输入,由隐层的输出
#(1,21).(21,1)=(1,1)
input2 = np.dot(output2, weight2).astype(np.float64)
# 输出层输出,由输出层的输入和阈值以及激活函数决定的,这里的阈值也可以放在输出层输入进行计算
# (1,1).(1,1)=(1,1)
output3 = sigmoid(input2 - value2).astype(np.float64)
# 更新公式由矩阵运算表示
#a:(1,1)
a = np.multiply(output3, 1 - output3)#输出层激活函数求导后的式子,multiply对应元素相乘,dot矩阵运算
#g:(1,1)
g = np.multiply(a, outputset - output3)#outputset - output3:实际标签和预测标签差
#weight2:(21,1),np.transpose(weight2):(1,21),b:(1,21)
b = np.dot(g, np.transpose(weight2))
#(1,21)
c = np.multiply(output2, 1 - output2)#隐层输出激活函数求导后的式子,multiply对应元素相乘,dot矩阵运算
#(1,21)
e = np.multiply(b, c)
value1_change = -x * e#(1,21)
value2_change = -x * g#(1,1)
weight1_change = x * np.dot(np.transpose(inputset), e)#(21,21)
weight2_change = x * np.dot(np.transpose(output2), g)#(21,1)
# 更新参数,权重与阈值的迭代公式
value1 += value1_change
value2 += value2_change
weight1 += weight1_change
weight2 += weight2_change
return weight1, weight2, value1, value2
2)dot、multiply
dot:两个矩阵按照行列相乘组成新的矩阵
multiply:两个矩阵和得到结果的矩阵的维度是一样的,对应位置的元素进行相乘得到新矩阵对应位置的元素值
3)难点
这一部分最大的难点就是在于读懂相关数学表达式的含义。建议将前面的理论部分之《待估参数的优化迭代公式》自己推导一遍,然后弄清楚这一部分中参数的维数,基本上就可以读懂了,代码中注释已经将所有参数的维数变化进行了标注。
6、测试模型
将最后得到的待估参数的值作为最终的神经网络的参数,对测试样本进行测试
#创建测试样本数据的函数
def testing(dataset1, labelset1, weight1, weight2, value1, value2):
# 记录预测正确的个数
rightcount = 0
for i in range(len(dataset1)):
# 计算每一个样例的标签通过上面创建的神经网络模型后的预测值
inputset = np.mat(dataset1[i]).astype(np.float64)
outputset = np.mat(labelset1[i]).astype(np.float64)
output2 = sigmoid(np.dot(inputset, weight1) - value1)
output3 = sigmoid(np.dot(output2, weight2) - value2)
# 确定其预测标签
if output3 > 0.5:
flag = 1
else:
flag = 0
if labelset1[i] == flag:
rightcount += 1
# 输出预测结果
print("预测为%d 实际为%d" % (flag, labelset1[i]))
# 返回正确率
return rightcount / len(dataset1)
7、主函数运行
def main():
#读取训练样本数据并且进行样本划分
dataset, labelset = loaddataset('./horseColicTraining.txt')
#读取测试样本数据并且进行样本划分
dataset1, labelset1 = loaddataset('./horseColicTest.txt')
#得到初始化的待估参数的值
weight1, weight2, value1, value2 = parameter_initialization(len(dataset[0]), len(dataset[0]), 1)
#迭代次数为1500次,迭代次数一般越大准确率越高,但是其运行时间也会增加
for i in range(1500):
#获得对所有训练样本训练迭代一次后的待估参数
weight1, weight2, value1, value2 = trainning(dataset, labelset, weight1, weight2, value1, value2)
#对测试样本进行测试,并且得到正确率
rate = testing(dataset1, labelset1, weight1, weight2, value1, value2)
print("正确率为%f" % (rate))
if __name__ == '__main__':
main()三、总结
1、几个循环
在本例中(单隐层),可以分为以下几个循环:
***通过行来遍历每一个样本的特征集和标签
for i in range(len(dataset)):#依次读取数据特征集中的元素,一个元素即为一个样本所含有的所有特征数据***迭代次数的循环,通过迭代次数来控制迭代的终止条件,当然也可以用while循环来进行迭代,用误差来控制迭代的终止
for i in range(1500):
#获得对所有训练样本训练迭代一次后的待估参数
weight1, weight2, value1, value2 = trainning(dataset, labelset, weight1, weight2, value1, value2)若是多隐层的话,还多一层循环:
***通过循环来遍历所有的隐层,一般遍历只是为了获得每一隐层的神经元的个数,因此只需要通过字典定义好每一隐层的神经元个数,然后通过遍历的方式获得神经元个数即可(注意神经元个数和权重、阈值个数的关系)。或者如果隐层的层数比较少,可以通过多添加几组待测参数即可,设有k层:
def parameter_initialization(x1,x2,...,xi,..., xk):
# 隐层阈值
value1 = np.random.randint(-5, 5, (x1, x2)).astype(np.float64)#随机生成(-5,5)之间的整数组成(1,y)的数组,然后再将其转为浮点数显示
# 输出层阈值
value2 = np.random.randint(-5, 5, (x1, x3)).astype(np.float64)
.........
valuei = np.random.randint(-5, 5, (x1, xi)).astype(np.float64)
.........
valuek = np.random.randint(-5, 5, (x1, xk+1)).astype(np.float64)
# 输入层与隐层的连接权重
weight1 = np.random.randint(-5, 5, (x1, x2)).astype(np.float64)
# 隐层与输出层的连接权重
weight2 = np.random.randint(-5, 5, (x2, x3)).astype(np.float64)
........
weighti = np.random.randint(-5, 5, (xi,xi+1)).astype(np.float64)
........
return weight1, weight2,...,weighti,...,weightk, value1, value2,...,valuei,...,valuek2、问题集锦
1)若是有多个输出怎么办?
若是有多个输出的话,只需要在主函数中修改输出层的神经元个数即可,神经元个数等于输出的个数,设有i个输出,输出的增多也意味着输出的归类判断会更加的复杂
weight1, weight2, value1, value2 = parameter_initialization(len(dataset[0]), len(dataset[0]), i)2)BP算法为什么叫做后向传播?
因为从目标函数对待测参数求偏导可以看出,目标函数对越往前的神经网络的参数进行求导,其要经过的层数就会越多,即要想求得目标函数对前面的参数的偏导,就必须先知道该层神经网络后面的层数中目标函数对待测参数的偏导,因为链式法则。而且在求对阈值的偏导的时候,我们需要注意的是,对该层阈值的偏导,受下一层所有神经元的影响,如下图就知道,每一层的神经元都互相有关系,所有每一层的神经元的阈值的偏导也和相邻层神经元有关
四、完整代码
#导入模块
import numpy as np
#创建加载数据读取数据以及划分数据集的函数,返回数据特征集以及数据标签集
def loaddataset(filename):
fp = open(filename)#(299,22)
# 存放数据
dataset = []
# 存放标签
labelset = []
for i in fp.readlines():#按照行来进行读取,每次读取一行,一行的数据作为一个元素存放在了类别中
a = i.strip().split()#去掉每一行数据的空格以及按照默认的分隔符进行划分
# 每个数据行的最后一个是标签
dataset.append([float(j) for j in a[:len(a) - 1]])#读取每一行中除最后一个元素的前面的元素,并且将其转换为浮点数
labelset.append(int(float(a[-1])))#读取每一行的最后一个数据作为标签数据
return dataset, labelset#dataset是(299,21)的列表,labelset是(299,1)的列表
# x为输入层神经元个数,y为隐层神经元个数,z输出层神经元个数
#创建的是参数初始化函数,参数有各层间的权重weight和阈值即偏置value就是b
#本例的x,y=len(dataset[0])=22,z=1
def parameter_initialization(x, y, z):
# 隐层阈值
value1 = np.random.randint(-5, 5, (1, y)).astype(np.float64)#随机生成(-5,5)之间的整数组成(1,y)的数组,然后再将其转为浮点数显示
# 输出层阈值
value2 = np.random.randint(-5, 5, (1, z)).astype(np.float64)
# 输入层与隐层的连接权重
weight1 = np.random.randint(-5, 5, (x, y)).astype(np.float64)
# 隐层与输出层的连接权重
weight2 = np.random.randint(-5, 5, (y, z)).astype(np.float64)
return weight1, weight2, value1, value2
#创建激活函数sigmoid
def sigmoid(z):
return 1 / (1 + np.exp(-z))
'''
weight1:输入层与隐层的连接权重
weight2:隐层与输出层的连接权重
value1:隐层阈值
value2:输出层阈值
权重和阈值的个数和神经网络的隐层层数有关,若隐层为n,则权重和阈值的个数为n+1
'''
#创建训练样本的函数,返回训练完成后的参数weight和value,这里的函数是经过一次迭代后的参数,即所有的样本经过一次训练后的参数
#具体参数的值可以通过设置迭代次数和允许误差来进行确定
def trainning(dataset, labelset, weight1, weight2, value1, value2):
# x为步长
x = 0.01#学习率
for i in range(len(dataset)):#依次读取数据特征集中的元素,一个元素即为一个样本所含有的所有特征数据
# 输入数据
#(1,21)
inputset = np.mat(dataset[i]).astype(np.float64)#每次输入一个样本,将样本的特征转化为矩阵,以浮点数显示
# 数据标签
#(1,1)
outputset = np.mat(labelset[i]).astype(np.float64)#输入样本所对应的标签
# 隐层输入,隐层的输入是由输入层的权重决定的,wx
#input1:(1,21).(21,21)=(1,21)
input1 = np.dot(inputset, weight1).astype(np.float64)
# 隐层输出,由隐层的输入和阈值以及激活函数决定的,这里的阈值也可以放在输入进行计算
#sigmoid((1,21)-(1,21))=(1,21)
output2 = sigmoid(input1 - value1).astype(np.float64)
# 输出层输入,由隐层的输出
#(1,21).(21,1)=(1,1)
input2 = np.dot(output2, weight2).astype(np.float64)
# 输出层输出,由输出层的输入和阈值以及激活函数决定的,这里的阈值也可以放在输出层输入进行计算
# (1,1).(1,1)=(1,1)
output3 = sigmoid(input2 - value2).astype(np.float64)
# 更新公式由矩阵运算表示
#a:(1,1)
a = np.multiply(output3, 1 - output3)#输出层激活函数求导后的式子,multiply对应元素相乘,dot矩阵运算
#g:(1,1)
g = np.multiply(a, outputset - output3)#outputset - output3:实际标签和预测标签差
#weight2:(21,1),np.transpose(weight2):(1,21),b:(1,21)
b = np.dot(g, np.transpose(weight2))
#(1,21)
c = np.multiply(output2, 1 - output2)#隐层输出激活函数求导后的式子,multiply对应元素相乘,dot矩阵运算
#(1,21)
e = np.multiply(b, c)
value1_change = -x * e#(1,21)
value2_change = -x * g#(1,1)
weight1_change = x * np.dot(np.transpose(inputset), e)#(21,21)
weight2_change = x * np.dot(np.transpose(output2), g)#(21,1)
# 更新参数,权重与阈值的迭代公式
value1 += value1_change
value2 += value2_change
weight1 += weight1_change
weight2 += weight2_change
return weight1, weight2, value1, value2
#创建测试样本数据的函数
def testing(dataset1, labelset1, weight1, weight2, value1, value2):
# 记录预测正确的个数
rightcount = 0
for i in range(len(dataset1)):
# 计算每一个样例的标签通过上面创建的神经网络模型后的预测值
inputset = np.mat(dataset1[i]).astype(np.float64)
outputset = np.mat(labelset1[i]).astype(np.float64)
output2 = sigmoid(np.dot(inputset, weight1) - value1)
output3 = sigmoid(np.dot(output2, weight2) - value2)
# 确定其预测标签
if output3 > 0.5:
flag = 1
else:
flag = 0
if labelset1[i] == flag:
rightcount += 1
# 输出预测结果
print("预测为%d 实际为%d" % (flag, labelset1[i]))
# 返回正确率
return rightcount / len(dataset1)
def main():
#读取训练样本数据并且进行样本划分
dataset, labelset = loaddataset('./horseColicTraining.txt')
#读取测试样本数据并且进行样本划分
dataset1, labelset1 = loaddataset('./horseColicTest.txt')
#得到初始化的待估参数的值
weight1, weight2, value1, value2 = parameter_initialization(len(dataset[0]), len(dataset[0]), 1)
#迭代次数为1500次,迭代次数一般越大准确率越高,但是其运行时间也会增加
for i in range(1500):
#获得对所有训练样本训练迭代一次后的待估参数
weight1, weight2, value1, value2 = trainning(dataset, labelset, weight1, weight2, value1, value2)
#对测试样本进行测试,并且得到正确率
rate = testing(dataset1, labelset1, weight1, weight2, value1, value2)
print("正确率为%f" % (rate))
if __name__ == '__main__':
main()参考:《机器学习 BP神经网络(Python实现)》写的很详细