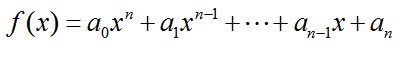多项式运算
多项式运算是数学中最基本的运算之一。在高等代数中,多项式一般可表示为以下形式:
对于这种表示形式,很容易用它的系数向量来表示,即
在MATLAB中正是用这样的系数向量来表示的。
一、多项式的构造
由以上分析可知,多项式可以直接用向量表示。因此,构造多项式最简单的方法就是直接输入向量。这种方法通过函数poly2sym来实现。其调用格式如下:
poly2sym(p)
其中p为多项式的系数向量。
>> p = [1 -2 5 6];
>> poly2sym(p)
ans =
x^3-2*x^2+5*x+6
>> 另外,也可以用多项式的根生成多项式。这种方法使用poly函数生成系数向量,再调用poly2sym函数生成多项式。
>> root = [-5 3+2i 3-2i];
>> p = poly(root)
p =
1 -1 -17 65
>> poly2sym(p)
ans =
x^3-x^2-17*x+65
>> 二、多项式的运算方法
1.多项式的四则运算
多项式的四则运算主要是多项式的加、减、乘、除运算。需要注意的是相加、减的两个向量必须大小相等。阶次不同时,低阶多项式必须用零填补,使其与高阶多项式有相同的阶次。多项式的加、减运算用“+”、”-”来实现,多项式的乘法用函数conv(p1,p2)来实现,相当于执行两个数组的卷积。多项式的除法用函数deconv(p1,p2)来实现,相当于执行两个数组的解卷。
>> p1 = [2 3 4 0 -2];
>> p2 = [0 0 8 -5 6];
>> p = p1 + p2;
>> poly2sym(p)
ans =
2*x^4+3*x^3+12*x^2-5*x+4
>> q = conv(p1, p2)
q =
0 0 16 14 29 -2 8 10 -12
>> poly2sym(q)
ans =
16*x^6+14*x^5+29*x^4-2*x^3+8*x^2+10*x-12>> p1 = [2 3 4 0 -2]
p1 =
2 3 4 0 -2
>> p2 = [1 3 5]
p2 =
1 3 5
>> p = deconv(p1, p2)
p =
2 -3 3
>> poly2sym(p)
ans =
2*x^2-3*x+3
>> 2.多项式的导数运算
多项式的导数运算用函数polyder来实现。其调用格式为:
polyder(p)
其中p为多项式的系数向量。
>> p = [4 3 2 1];
>> poly2sym(p)
ans =
4*x^3+3*x^2+2*x+1
>> q = polyder(p)
q =
12 6 2
>> poly2sym(q)
ans =
12*x^2+6*x+2
>> 3.估值运算
多项式的估值运算用
调用格式 说明
polyval(p,s) p为多项式的系数向量,s为向量或者矩阵,它是按数组运算规则来求多项式的值
polyvalm(p,s) p为多项式的系数向量,s为方阵,它是按矩阵运算规则来求多项式的值
>> p1 = [2 5 0 4 1 4];
>> h = polyval(p1, [2 5])
h =
166 9484
>> j = polyval(p1, [2 5;1 2])
j =
166 9484
16 166
>> k = polyvalm(p1, [2 5;1 2])
k =
2211 4935
987 2211
>> help polyvalm
POLYVALM Evaluate polynomial with matrix argument.
Y = POLYVAL(P,X), when P is a vector of length N+1 whose elements
are the coefficients of a polynomial, is the value of the
polynomial evaluated with matrix argument X. X must be a
square matrix.
Y = P(1)*X^N + P(2)*X^(N-1) + ... + P(N)*X + P(N+1)*I
Class support for inputs p, X:
float: double, single
See also polyval, polyfit.
Reference page in Help browser
doc polyvalm
>> 4.求根运算
求根运算用函数roots。
>> p1
p1 =
2 5 0 4 1 4
>> poly2sym(p1)
ans =
2*x^5+5*x^4+4*x^2+x+4
>> r = roots(p1)
r =
-2.7709
0.5611 + 0.7840i
0.5611 - 0.7840i
-0.4257 + 0.7716i
-0.4257 - 0.7716i
>> 三、多项式拟合
多项式拟合用polyfit函数来实现,其调用格式如下:
调用格式 说明
polyfit(x,y,n) 表示二乘法对已知数据x、y进行拟合,以求得n阶多项式系数向量
[p,s]=polyfit(x,y,n) p为拟合多项式系数向量,s为拟合多项式系数向量的信息结构
x =
0 0.1571 0.3142 0.4712 0.6283 0.7854 0.9425 1.0996 1.2566 1.4137 1.5708
>> y = sin(x)
y =
0 0.1564 0.3090 0.4540 0.5878 0.7071 0.8090 0.8910 0.9511 0.9877 1.0000
>> [p,s] = polyfit(x,y,5)
p =
0.0057 0.0060 -0.1721 0.0021 0.9997 0.0000
s =
R: [6x6 double]
df: 5
normr: 1.6712e-005
>>