算法：哈夫曼编码算法（Java）

1、问题描述

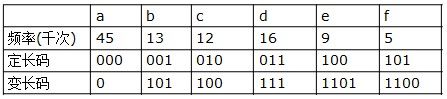
  哈夫曼编码是广泛地用于数据文件压缩的十分有效的编码方法。其压缩率通常在20%～90%之间。哈夫曼编码算法用字符在文件中出现的频率表来建立一个用0，1串表示各字符的最优表示方式。一个包含100,000个字符的文件，各字符出现频率不同，如下表所示。

有多种方式表示文件中的信息，若用0,1码表示字符的方法，即每个字符用唯一的一个0,1串表示。若采用定长编码表示，则需要3位表示一个字符，整个文件编码需要300,000位；若采用变长编码表示，给频率高的字符较短的编码；频率低的字符较长的编码，达到整体编码减少的目的，则整个文件编码需要（45×1+13×3+12×3+16×3+9×4+5×4）×1000=224,000位，由此可见，变长码比定长码方案好，总码长减小约25%。

 前缀码：对每一个字符规定一个0,1串作为其代码，并要求任一字符的代码都不是其他字符代码的前缀。这种编码称为前缀码。编码的前缀性质可以使译码方法非常简单；例如001011101可以唯一的分解为0,0,101,1101，因而其译码为aabe。

 译码过程需要方便的取出编码的前缀，因此需要表示前缀码的合适的数据结构。为此，可以用二叉树作为前缀码的数据结构：树叶表示给定字符；从树根到树叶的路径当作该字符的前缀码；代码中每一位的0或1分别作为指示某节点到左儿子或右儿子的“路标”。

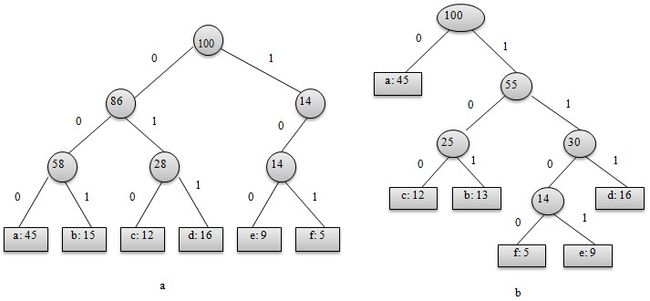
 从上图可以看出，表示最优前缀码的二叉树总是一棵完全二叉树，即树中任意节点都有2个儿子。图a表示定长编码方案不是最优的，其编码的二叉树不是一棵完全二叉树。在一般情况下，若C是编码字符集，表示其最优前缀码的二叉树中恰有|C|个叶子。每个叶子对应于字符集中的一个字符，该二叉树有|C|-1个内部节点。

 给定编码字符集C及频率分布f,即C中任一字符c以频率f(c)在数据文件中出现。C的一个前缀码编码方案对应于一棵二叉树T。字符c在树T中的深度记为dT(c)。dT(c)也是字符c的前缀码长。则平均码长定义为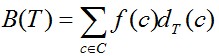：![这里写图片描述](https://img-blog.csdn.net/20151220143712799)使平均码长达到最小的前缀码编码方案称为C的最优前缀码。     


 2、构造哈弗曼编码

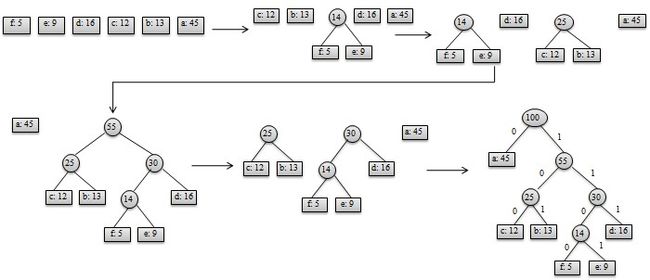
 哈夫曼提出构造最优前缀码的贪心算法，由此产生的编码方案称为哈夫曼编码。其构造步骤如下：

 (1)哈夫曼算法以自底向上的方式构造表示最优前缀码的二叉树T。

 (2)算法以|C|个叶结点开始，执行|C|－1次的“合并”运算后产生最终所要求的树T。

 (3)假设编码字符集中每一字符c的频率是f(c)。以f为键值的优先队列Q用在贪心选择时有效地确定算法当前要合并的2棵具有最小频率的树。一旦2棵具有最小频率的树合并后，产生一棵新的树，其频率为合并的2棵树的频率之和，并将新树插入优先队列Q。经过n－1次的合并后，优先队列中只剩下一棵树，即所要求的树T。

  构造过程如图所示：

/*-------------------------------------------------------------------------
 * Name:   哈夫曼编码源
 * Date:   2015.12.20
 * Author: Ingrid 
 * 实现过程：
 *      //初始化huffmanTree,huffmanCode
 *      initHuffmanTree(huffmanTree,m);
 *      initHuffmanCode(huffmanCode,n);
 *      
 *      //获取huffmanCode的符号
 *      getHuffmanCode(huffmanCode,n);
 *
 *      //获取huffmanTree的频数
 *      getHuffmanWeight(huffmanTree,n);
 *      
 *      //创建huffmanTree
 *      createHaffmanTree(huffmanTree,n);
 *      //创建huffmanCode
 *      createHaffmanCode(huffmanTree,huffmanCode,n);
 *      
 *      //输出huffmanCode编码
 *      ouputHaffmanCode(huffmanCode,n);    
 *------------------------------------------------------------------------*/


import java.util.Scanner;
public class HuffmanCode{
    //建立数的节点类
    static class Node{
        int weight;//频数
        int parent;
        int leftChild;
        int rightChild;

        public Node(int weight,int parent,int leftChild,int rightChild){
            this.weight=weight;
            this.parent=parent;
            this.leftChild=leftChild;
            this.rightChild=rightChild;
        }

        void setWeight(int weight){
            this.weight=weight;
        }

        void setParent(int parent){
            this.parent=parent;
        }

        void setLeftChild(int leftChild){
            this.leftChild=leftChild;
        }

        void setRightChild(int rightChild){
            this.rightChild=rightChild;
        }

        int getWeight(){
            return weight;
        }

        int getParent(){
            return parent;
        }

        int getLeftChild(){
            return leftChild;
        }

        int getRightChild(){
            return rightChild;
        }
    }

    //新建哈夫曼编码
    static class NodeCode{
        String character;
        String code;
        NodeCode(String character,String code){
            this.character=character;
            this.code=code;
        }
        NodeCode(String code){
            this.code= code;
        }

        void setCharacter(String character){
            this.character=character;
        }

        void setCode(String code){
            this.code=code;
        }

        String getCharacter(){
            return character;
        }

        String getCode(){
            return code;
        }
    }

    //初始化一个huffuman树
    public static void initHuffmanTree(Node[] huffmanTree,int m){
        for(int i=0;inew Node(0,-1,-1,-1);
        }
    }

    //初始化一个huffmanCode
    public static void initHuffmanCode(NodeCode[] huffmanCode,int n){
        for(int i=0;inew NodeCode("","");
        }
    }

    //获取huffmanCode的符号
    public static void getHuffmanCode(NodeCode[] huffmanCode , int n){
        Scanner input = new Scanner(System.in);
        for(int i=0;inew NodeCode(temp,"");
        }
    }

    //获取huffman树节点频数
    public static void getHuffmanWeight(Node[] huffmanTree , int n){
        Scanner input = new Scanner(System.in);
        for(int i=0;iint temp = input.nextInt();
            huffmanTree[i] = new Node(temp,-1,-1,-1);
        }
    }

    //从n个结点中选取最小的两个结点
    public static int[] selectMin(Node[] huffmanTree ,int n)  
    {  
        int min[] = new int[2];
          class TempNode
           {  
                  int newWeight;//存储权  
                  int place;//存储该结点所在的位置  

                  TempNode(int newWeight,int place){
                      this.newWeight=newWeight;
                      this.place=place;
                  }

                  void setNewWeight(int newWeight){
                      this.newWeight=newWeight;
                  }

                  void setPlace(int place){
                      this.place=place;
                  }

                  int getNewWeight(){
                      return newWeight;
                  }

                  int getPlace(){
                      return place;
                  }
           } 

           TempNode[] tempTree=new TempNode[n];  

         //将huffmanTree中没有双亲的结点存储到tempTree中 
           int i=0,j=0;   
           for(i=0;iif(huffmanTree[i].getParent()==-1&& huffmanTree[i].getWeight()!=0)  
                  {  
                      tempTree[j]= new TempNode(huffmanTree[i].getWeight(),i);  
                      j++;  
                  }  
           } 

           int m1,m2;  
           m1=m2=0;  
           for(i=0;iif(tempTree[i].getNewWeight()//此处不让取到相等，是因为结点中有相同权值的时候，m1取最前的   
                         m1=i;  
           }  
           for(i=0;iif(m1==m2)  
                         m2++;//当m1在第一个位置的时候，m2向后移一位  
                  if(tempTree[i].getNewWeight()<=tempTree[m2].getNewWeight()&& i!=m1)//此处取到相等，是让在结点中有相同的权值的时候，  

                                       //m2取最后的那个。  
                         m2=i;  
           }  

           min[0]=tempTree[m1].getPlace();  
           min[1]=tempTree[m2].getPlace();  
       return min;
    }  

    //创建huffmanTree
    public static void createHaffmanTree(Node[] huffmanTree,int n){   
           if(n<=1)  
               System.out.println("Parameter Error!");  
           int m = 2*n-1; 
           //initHuffmanTree(huffmanTree,m);  

           for(int i=n;iint[] min=selectMin(huffmanTree,i);
               int min1=min[0];
               int min2=min[1];
               huffmanTree[min1].setParent(i);  
               huffmanTree[min2].setParent(i);  
               huffmanTree[i].setLeftChild(min1);  
               huffmanTree[i].setRightChild(min2);
               huffmanTree[i].setWeight(huffmanTree[min1].getWeight()+ huffmanTree[min2].getWeight());   
           }  
    }

    //创建huffmanCode
    public static void createHaffmanCode(Node[] huffmanTree,NodeCode[] huffmanCode,int n){
        Scanner input = new Scanner(System.in);
        char[] code = new char[10]; 
        int start;
        int c;
        int parent;
        int temp;

        code[n-1]='0'; 
        for(int i=0;inew StringBuffer();
            start=n-1;
            c=i;
            while( (parent=huffmanTree[c].getParent()) >=0 )  
                  {  
                         start--;  
                         code[start]=((huffmanTree[parent].getLeftChild()==c)?'0':'1');  
                         c=parent;  

                  } 
            for(;start1;start++){
                 stringBuffer.append(code[start]);
            }
            huffmanCode[i].setCode(stringBuffer.toString());
           }
    }

    //输出hufmanCode
    public static void ouputHaffmanCode(NodeCode[] huffmanCode,int n){
        System.out.println("字符与编码的对应关系如下：");
        for(int i=0;iout.println(huffmanCode[i].getCharacter()+":"+huffmanCode[i].getCode());
        }
    }

    //主函数
    public static void main(String[] args){
        Scanner input = new Scanner(System.in);
        int n;
        int m;
        System.out.print("请输入字符个数：");
        n = input.nextInt();
        m=2*n-1;
        Node[] huffmanTree = new Node[m];
        NodeCode[] huffmanCode = new NodeCode[n];

        //初始化huffmanTree,huffmanCode
        initHuffmanTree(huffmanTree,m);
        initHuffmanCode(huffmanCode,n);

        //获取huffmanCode的符号
        System.out.print("请输入哈夫曼编码的字符：");
        getHuffmanCode(huffmanCode,n);

        //获取huffmanTree的频数
        System.out.print("请输入哈夫曼编码字符对应的频数：");
        getHuffmanWeight(huffmanTree,n);

        //创建huffmanTree
        createHaffmanTree(huffmanTree,n);
        //创建huffmanCode
        createHaffmanCode(huffmanTree,huffmanCode,n);

        //输出huffmanCode编码
        ouputHaffmanCode(huffmanCode,n);

    }   
}