Integration of omic networks in a developmental atlas of maize 笔记

文章于2016年发表于 Science 上。研究阐述了以现有手段测得的各组学数据间相关性较弱，难以通过单一的组学数据来推测生物体内可能的调控结构，作者提出通过多组学数据相结合的方法来提高转录因子推测的可信度，为预测转录因子提供了新思路。

随着转录组学、蛋白组学研究的深入，研究人员发现：生物体内 mRNA 含量与其所对应的蛋白质含量之间相关性较弱。（However, genome-wide correlations between the levels of proteins and mRNAs are weakly positive）所以我们很难通过对生物体 mRNA 含量的测定来准确推测对应蛋白质含量。作者以玉米为研究目标，测定了转录组、蛋白组和磷酸蛋白组数据，详细研究了各组学数据之间的关系及可能存在的应用。

作者首先用 pearson 相关系数评估了各组学数据在生物重复之间的相关性：**转录组、蛋白组、磷酸蛋白组分别为 0.9、0.84、0.7。相关性总体较高，说明样本间变量基本得到控制，被检测出来的物质含量基本稳定，随机误差较小。**但从被检出物质的分布上来看，mRNA 组出现了双峰，而两个蛋白组只有单峰，且与 mRNA 高丰度区（右峰）重合。（nearly all proteins and phosphoproteins arising from the 34,455 transcripts in the high-abundance population (right peak)）（fig 1）转录组学数据测定相对于蛋白组学更敏感可以作为解释该现象的部分原因。

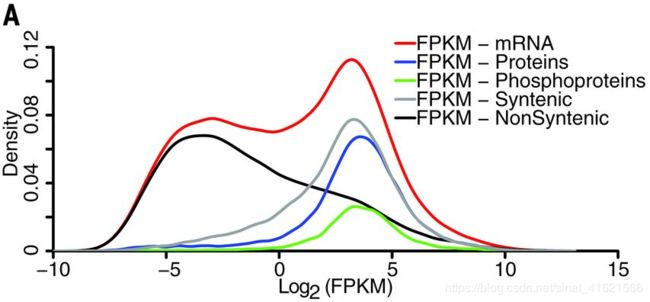
另一方面，在 mRNA 的高丰度区中也只检测到 46% 的 mRNA 有对应的蛋白质。造成该结果可能的原因有：（i）mRNA 和蛋白质稳定性的差异；（ii）蛋白质在组织间的运输；（iii）mRNAs 和对应蛋白质存在时间上的异相积累；（iiii）部分 mRNA 可能不编码蛋白质。

在与高粱的比较中发现：（i）同源基因的 mRNA 含量丰度较高，而非同源则较低；（ii）同源区内基因可翻译出蛋白质的可能性是非同源区的 9 倍。但第二条结论可能是由于非同源区基因转录的 mRNA 含量较低，所以翻译出的蛋白质可能未被检测到。作者研究了不同 mRNA 丰度下同源区和非同源区基因，结果均与第二条结论相似。所以该结论与 mRNA 丰度无关，同源区中有更多的基因表达蛋白并参与到生理功能的建设中，非同源区中有更多的基因只转录 mRNA，可能参与到生理功能的调控中。可以推论出同源区基因的突变更易引起生物体生理功能的缺陷，而非同源区基因突变更易引起调控的失常。这可能是“引发玉米表型上出现可观的变异所对应的突变主要存在于同源保守基因中（ 8 倍富集）”这一现象的一种解释。

接着，作者利用 WGCNA（weighted gene coexpression network analysis，加权基因共表达网络分析）R包根据转录组学数据，计算基因间相关系数（Spearman correlations）并分层聚类，将基因聚类成了多个模块。再利用 MapMan 对每个模块中的基因功能进行注释，以模块中富集的功能基因作为该模块的功能标签。对蛋白组和磷酸蛋白组数据进行同样的操作。可以想象，由于组学数据之间的低相关性，同一个基因在不同组学数据的分析中，可能被聚类到不同功能标签的模块中。作者研究了不同组学数据分析下，相同功能标签的模块间基因的重叠率。（fig 2）大部分模块的重叠率都较低。说明相同的生理功能在不同的网络中，由不同的基因来挑大梁，你方唱罢我登场。

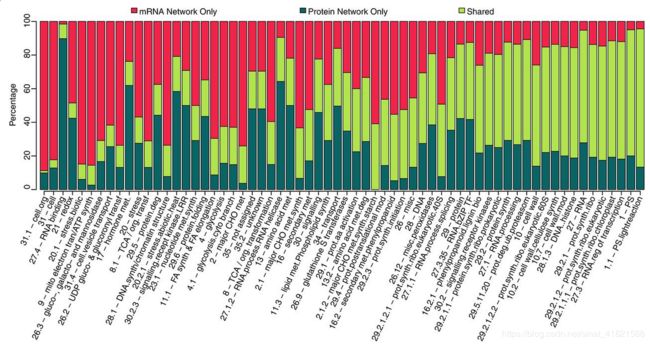
WGCNA 在利用相关系数进行分层聚类的同时，还绘制了共表达网络。作者以 0.75 作为阈值，提取网络中相关性得分 > 0.75 的连接，重建共表达网络，并比较了转录组与蛋白组数据下的重建共表达网络间的相似性。发现在两个网络的并集，总计约200万条连接中，交集约12万条连接，即 Jaccard 系数等于 6.1%。当降低阈值使两个重建共表达网络并集连接数达到1000万时，结论不变。不同网络中行驶相同功能的基因不同，可能为这一现象做出部分解释。

PS：无尺度网络
网络由节点（node）和连接（link）构成。节点的连接数 k 表示了该节点在网络中的重要性，k越大，节点越重要。若网络各节点之间的连接是随机生成的，那么节点的连接数 k 应当服从泊松分布或正态分布。当网络中节点连接数 k 是可估计的时候，这类网络称之为有尺度网络。人们一开始认为互联网是有尺度网络，因为网民对网站的访问，是独立、自由的，完全取决于网民本人的主观意愿，每个网站的被访问量差异不会太大。但实际结果为：在绝大多数网站的连接数很少的背景下，有极少数网站拥有高于普通网站百倍、千倍甚至万倍的连接数，这些节点的连接数无法估计。研究发现，互联网中连接数为 k 的节点的出现概率反比于 k 的 n 次方，即 p(k) ∝ 1/(k^n)，其中 n 为常数。统计物理学家一般把服从幂律分布的现象称为无尺度现象，用“无尺度”来形容难以预料。所以当网络中节点的连接数 k 与节点出现概率 p 之间服从幂律分布时，该网络称之为无尺度网络。研究发现，万维网、人际关系网络、神经网络、细胞网络等均可不同程度的视为无尺度网络。
上述内容摘自《李幼平:无尺度现象引发的思考》

PS：WGCNA 算法简介
WGCNA分为表达量聚类分析和表型关联两部分，主要包括基因之间相关系数计算、基因模块的确定、共表达网络、模块与性状关联四个步骤。

1. 计算任意两个基因之间的pearson相关系数。
2. 遍历幂 S，寻找合适的取值，用相关系数的 S 次幂作为权重来构建网络。 因为WGCNA前提假设生物网络符合无尺度网络，所以利用相关系数构建出的网络需要符合无尺度网络的特性。由于直接使用相关系数构建出的网络无法满足无尺度的特性，WGCNA对相关系数乘以 S 次幂来强化强相关，弱化弱相关，通过遍历 S 的可能取值（图中取值为1-30），寻找适当的取值使网络满足无尺度。

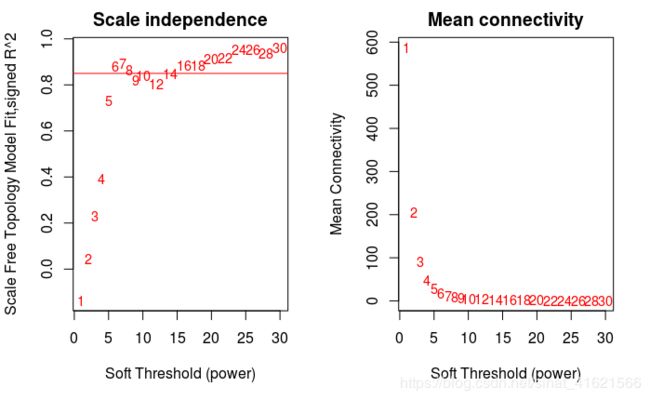
如图 fig PS1，横轴表示 Soft Threshold 的取值，即 S 的取值。左图纵轴代表网络中节点 K 的连接数 k 的对数 log(k) 与 出现概率 p(k) 的对数 log(p(k)) 的相关系数 R 的平方。∵ p(k) ∝ 1/(kⁿ)，∴ log(p(k)) ∝ -nlog(k)，∴ log(p(k)) ∝ -log(k)，相关系数的平方越高，说明该网络越逼近无网路尺度的分布。本例中以 R² = 0.85 作为阈值，确定 S 的取值为 6。右图纵轴代表网络中节点 K 的平均连接数，随着 S 值的不断增加，弱相关被弱化，原先存在的连接不断消失，平均连接数不断降低。相关系数的 S 次幂所构建的矩阵。
3. 通过基因间的权重进行分层聚类。聚类结果中不同的分支代表不同的基因模块，不同颜色代表不同的模块。（fig PS2）

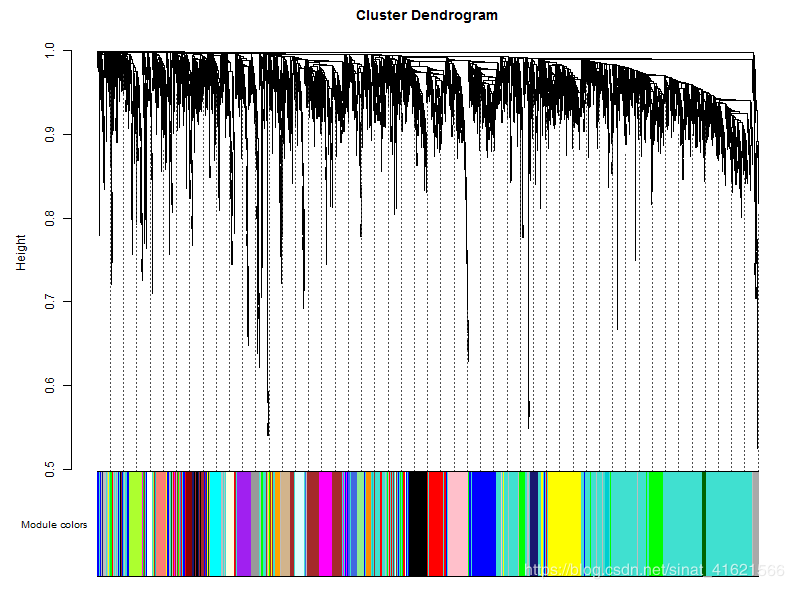关于 WGCNA 更详尽的用法及原理介绍，参见一文学会WGCNA分析 或 WGCNA分析，简单全面的最新教程

作者又比较了生物学重复之间，相同组学数据下的重建共表达网络之间的相似性。发现转录组学数据下，生物学重复之间的网络的 Jaccard 系数为 46%，蛋白组学为 36%。在物质测定较为准确的背景下（同一物质的含量于生物学重复之间的相关系数可以达到 0.9、0.84、0.7），物质之间的相关系数稳定性却较低，说明网络内不仅存在两两之间的直接调控，还存在着大量二级、三级等的多级调控，或称为间接调控。多级调控也可能为不同组学共表达网络间低 Jaccard 系数现象做出部分解释。

由于共表达网络符合无尺度网络的特定，作者以网络中连接数前10%的节点作为核心节点（hub），比较了不同组学下共表达网络hub的相似性。研究发现两个网络中只有15%的 hub 是共享的。此结论也证实了不同组学网络的不相似性。（fig 3）

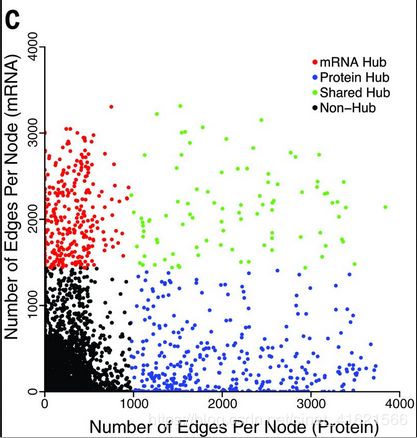
综上，无论是组学数据内的相关系数，如基因A 的 mRNA 含量 与 基因B 的 mRNA 含量的相关系数，还是组学数据间的相关系数，如基因A 的 mRNA 含量 与 基因A 的 蛋白质 含量的相关系数，稳定性都低，我们难以通过基因的一组组学数据来预测另一组组学数据。

不同组学数据下的共表达网络的整体间的相关性差，如果缩小范围，只观察网络中的局部，是否相关性会提高？已知转录因子对基因的表达有着重要的作用，转录因子与靶基因间的相关性是否稳定？作者利用基因调控网络（gene regulatory networks，GRNs）研究了组学数据与转录因子之间的关系。

PS：共表达网络与基因调控网络的区别
共表达网络是计算集合内两两间相关系数，利用相关系数构建网络，网络是无向的。GRNs 由两个集合构建而成，一个是转录因子集合，一个是靶基因集合，计算转录因子与靶基因间的相关性。其中靶基因集合可以是基因对应的转录组数据，也可以是对应的蛋白组数据。虽然也是利用相关系数构建网络，但网络是有向的，从转录因子指向靶基因，即转录因子调控靶基因。

作者利用 GENIE3 构建 GRNs。用已知的、研究清楚的转录因子 KN1 和 O2 作为验证集，验证GENIE3 所构建出的 GRNs 的准确性。具体来说，将 GENIE3 预测 KN1、O2 生成出的 GRNs 中评分前 500 的连接指向的靶基因与真实的靶基因对比，KN1 的 GRNs 准确预测出了 108（mRNA）、129（蛋白质）、125（磷酸肽）靶基因，O2 结果与 KN1 类似。fig 4B 展示了 KN1 各组学数据预测出的靶基因之间的关系。可以发现， 3 个组学数据总共准确预测出了 195 个靶基因，其中有 86 个（44%）靶基因是各组学数据独自预测出的，多组学数据间存在互补。当将分析范围扩展都全部转录因子时，取各组学 GRNs 中评分前 100万 的连接，发现有 93% 的靶基因是非重合的（fig 4C）。所以作者提出可以利用多组学数据提升预测转录因子的靶基因的准确性。

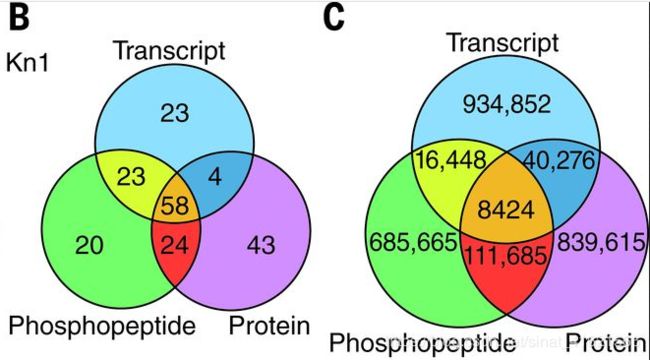
PS：GENIE3 算法简介
输入：目标基因集合和输入基因集合
输出：目标基因指向输入基因的有向网络，即 GRNs
步骤：（i）用输入基因的表达模式预测目标基因，预测的方法为随机森林算法。p 个目标基因会得到 p 个模型；（ii）根据阈值，若 输入基因A 在模型中的信息增益大于阈值，则建立 目标基因X 与 输入基因A 之间的连接，通过模型得到由目标基因指向输入基因的有向网络。p 个基因会生成 p 个有向网络；（iii）若目标基因集合与输入基因集合有交集，说明部分目标基因可能作为输入基因时与其他目标基因建立了连接，所以需要对着 p 个有向网络进行整合，构建 GRNs；若无交集则无需整合，这 p 个有向网络即为 GRNs。
本研究中以 3186 个转录因子作为目标基因，41021 个基因作为输入基因，两集合间无交集。输入基因中能与转录因子建立连接的，将其作为该转录因子的靶基因，最后生成了 3186 个有向网络。

为了防止多组学数据的整合引入真阳性的同时引入更多的假阳性，作者仍以 KN1 和 O2 作为验证集，绘制了不同组学数据预测出的 GRNs 的 ROC 曲线（fig 5）。可以发现，整合多组学数据的预测效果优于单组学数据。如，研究者希望使用假阳性率为20%的网络预测，则 mRNA 构建的 GRNs 网络仅能预测出 40% 的真阳性，而组合网络为 50%。

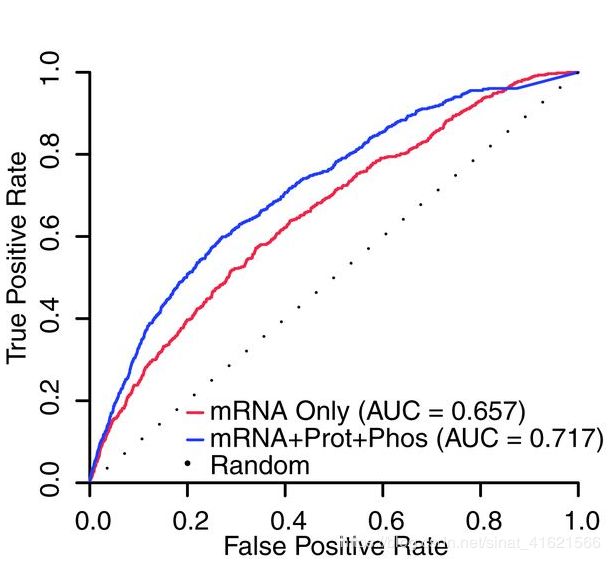
上述数据测定的都来自玉米 B73 株系，作者又测定了 Mo17 株系中各组学数据。数据中绝大部分转录因子在不同株系间表达量处于相同的数量级上，但也有少部分（149 mRNA、26 蛋白质、16 磷酸肽）出现了显著差异。作者对出现显著性差异的转录因子构建了 GRNs，比较不同株系相同转录因子对应靶基因间的异同。（fig 6）发现其中少数转录因子所对应的靶基因在不同株系间表达量存在显著差异，作者推测：转录因子的表达量与 GRNs 之间是相对稳定（保守）的，若表达量发生了显著性变化，可能转录因子的调控模式发生了改变；同一个转录因子在不同株系间可能有不同的调控模式。该推论有局限性，因为作者没有比较表达量处于相同数量级上的转录因子的靶基因间表达量发生显著性变化的比例。如果也有 40% 左右的转录因子的靶基因的表达量有显著性差异，那么这个推论就没有意义了。

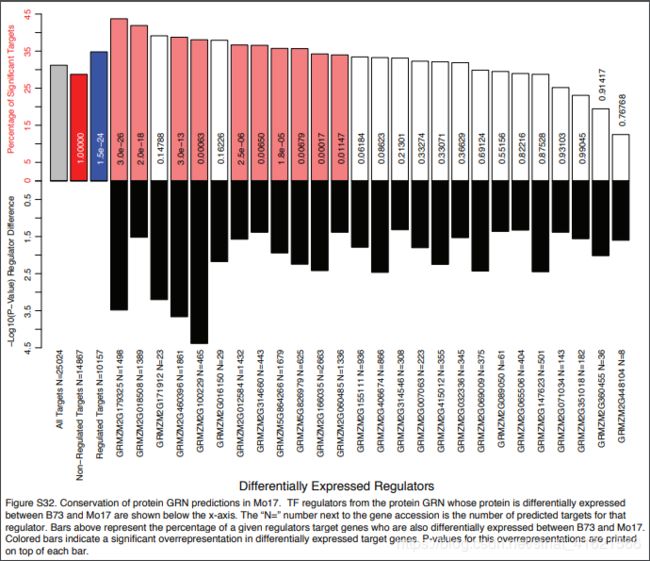
综上全部，研究阐述了以现有手段测得的各组学数据间相关性较弱，难以通过单一的组学数据来推测生物体内可能的调控结构，作者提出通过多组学数据相结合的方法来提高转录因子推测的可信度，为预测转录因子提供了新思路。