数据结构之线段树入门（单点更新&&区间查询）

线段树是学习数据结构必须学习的一种数据结构，在ACM，蓝桥等比赛中是经常出现的。利用线段树解题，会使得题目简单易理解。而且线段树是数据结构中比较基础而且用的很多的一种。

线段树定义

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。
对于线段树中的每一个非叶子节点[a,b]，它的左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树，最后的子节点数目为N，即整个线段区间的长度。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN）。而未优化的空间复杂度为2N，因此有时需要离散化让空间压缩。

线段树图示

线段树解决什么问题

线段树解决的是区间的问题，顾名思义，线段，就代表着一段区间上的问题。而线段树则是通过树这种数据结构来解决区间的问题。但是区间问题除了用线段树，也可以用别的方式来解决。那么线段树有什么特别之处呢？线段树可以解决带有更改的区间问题。最基础的是两种，区间求最值以及区间求和。

线段树的基本内容

线段树绝对不只是为了解决区间问题的数据结构，事实上，是线段树多用于解决区间问题，并不是线段树只能解决区间问题，首先，我们得先明白几件事情。

每个结点存什么，结点下标是什么，如何建树。
我们以区间求最值来阐述这个问题。

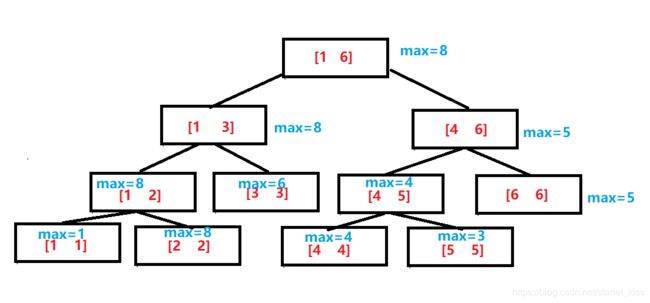
A数组为[1,8,6,4,3,5].在求最大值的线段树上建树后的分布如上图所示。
可以发现，每个叶子结点的值就是数组的值，每个非叶子结点的度都为二，且左右两个孩子分别存储父亲一半的区间。每个父亲的存储的值也就是两个孩子存储的值的最大值。
我们现在想的是每个节点如何存储数据以及我们怎么能够快速的找到某个节点的孩子节点以及父亲节点呢？这也就是线段树的重点和难以理解的地方了。
对于一个区间[l,r]来说，最重要的数据当然就是区间的左右端点l和r，但是大部分的情况我们并不会去存储这两个数值，而是通过递归的传参方式进行传递。这种方式用指针好实现，定义两个左右子树递归即可，但是指针表示过于繁琐，而且不方便各种操作，大部分的线段树都是使用数组进行表示，那这里怎么快速使用下标找到左右子树呢。我们对上图每一个存储结构编号。如下图所示：

值得一问的是，为什么最下一排的下标直接从9跳到了12，道理也很简单，中间其实是有两个空间的呀！！虽然没有使用，但是他已经开了两个空间，这也是为什么无优化的线段树建树需要4倍的存储空间，一般会开到4 * n的空间防止RE。
从上图我们可以看到，假设节点为cur，那么它的左孩子节点为（2 * cur），右孩子节点为（2 * cur+1）。因为左子树都是偶数，所以我们常用位运算来寻找左右子树。
k<<1（结点k的左子树下标）
k<<1|1（结点k的右子树下标）
明白了一些基本的常识，那就要学着建树了。

const int maxx=1e6+1;
int ary[maxx];

struct node
{
	int l,r,n;
}a[maxx<<2];//开设四倍空间
inline void pushup(int cur)//pushup函数的意思是：我们更新了两个孩子节点的最值了，那么我们就可以通过两个孩子节点的值来更新父亲节点的值了。
{
	a[cur].n=max(a[cur<<1].n,a[cur<<1|1].n);
	//a[cur].n=a[cur<<1].n+a[cur<<1|1].n，如果是区间求和的话就这么写。
}

void build(int l,int r,int cur)
{
	int m=(l+r)>>1;//取中
	a[cur].n=0;//初始化
	a[cur].l=l,a[cur].r=r;//规定区间的最左端和最右端
	if(l==r)//到达叶子节点了
	{
		a[cur].n=ary[l];
		return ;
	}
	build(l,m,cur<<1);//递归去建树，这里运用了二分的思想
	build(m+1,r,cur<<1|1);
	pushup(cur);//建完树之后就往上更新。
}

线段树的基本操作

这种在线的树结构，一般就是两种操作，更新和查询。
①点更新
如何实现点更新，我们先不急看代码，还是对于上面那个线段树，假使我把a[3]+7，则更新后的线段树应该变成

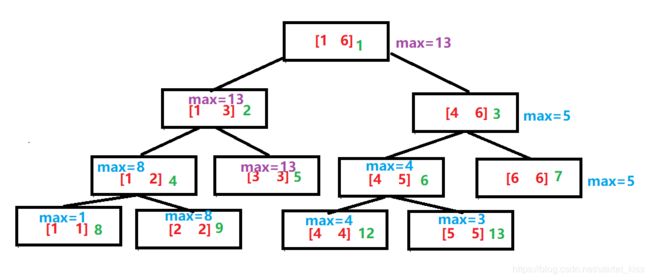
更新了a[3]后，则每个包含此值的结点都需要更新，那么有多少个结点需要更新呢？根据二叉树的性质，不难发现是log(k)个结点，这也正是为什么每次更新的时间复杂度为O(logN)，那应该如何实现呢，我们发现，无论你更新哪个叶子节点，最终都是会到根结点的，而把这个往上推的过程逆过来就是从根结点开始，找到左子树还是右子树包含需要更新的叶子节点，往下更新即可，所以我们还是可以使用递归的方法实现线段树的点更新。
update代码如下：

inline void update(int l,int r,int v,int cur,int pos)
{
	int L=a[cur].l;
	int R=a[cur].r;//找出这个区间的左右端点
	if(L==R)//如果到达了叶子节点的话，更新后返回就可以了。
	{
		a[cur].n+=v;
		return ;
	}
	int mid=L+R>>1;//找到这个节点的中点
	if(pos<=mid) update(l,mid,v,cur<<1,pos);//左区间
	else update(mid+1,r,v,cur<<1|1,pos);//右区间
	pushup(cur);//往上更新
}

②区间查询
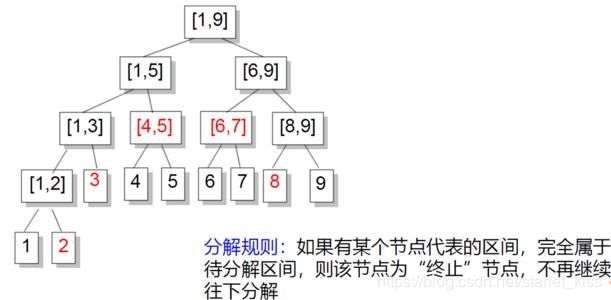
说完了单点更新肯定就要来说区间查询了，我们知道线段树的每个结点存储的都是一段区间的信息 ，如果我们刚好要查询这个区间，那么则直接返回这个结点的信息即可，比如对于上面线段树，如果我直接查询[1,6]这个区间的最值，那么直接返回根节点信息返回13即可，但是一般我们不会凑巧刚好查询那些区间，比如现在我要查询[2,5]区间的最值，这时候该怎么办呢，我们来看看哪些区间是[2,5]的真子集。如下图所示

画黄颜色的就是[2,5]的真子集，但是我们可以看到[4,4]和[5,5]是被[4,5]包括的，而且[4,5]的最值我们也是知道的，这样我们就只查寻三个区间就可以了。我们还是从根节点开始往下递归，如果当前结点是要查询的区间的真子集，则返回这个结点的信息且不需要再往下递归了，这样从根节点往下递归，时间复杂度也是O(logN)。
代码如下：

inline int query(int l,int r,int cur)
{
	int L=a[cur].l;
	int R=a[cur].r;
	if(l<=L&&R<=r) return a[cur].n;//如果查询的区间包含当前结构的区间的话，就直接返回当前结构的最大值就可以了
	int mid=L+R>>1;
	if(r<=mid) return query(l,r,cur<<1);//如果查询的区间在当前结构区间的左半段。
	else if(mid>l) return query(l,r,cur<<1|1);//如果查询的区间在当前结构区间的右半段。
	else return max(query(l,mid,cur<<1),query(mid+1,r,cur<<1|1));//上两种情况不成立，就要分开讨论两种情况取最优值了。
}

线段树的基本操作就是这些了。自己动手模拟一下然后多做题就能掌握了。
参考博客：https://www.cnblogs.com/xenny/p/9801703.html
努力加油a啊，(^o)/~