程序员的机器学习入门笔记（六）：决策树的入门介绍

介绍

历史背景

决策树算法是最早的机器学习算法之一。早在 1966 年 Hunt,Marin 和 Stone 提出的CLS 学习系统就有了决策树算法的概念。但到了 1979 年， J.R. Quinlan 才给出了 ID3算法的原型， 1983 年和 1986 年他对 ID3 算法进行了总结和简化，正式确立了决策树
学习的理论。 从机器学习的角度来看，这是决策树算法的起点。到 1986 年， Schlimmer和 Fisher 在此基础上进行改造，引入了节点缓冲区，提出了 ID4 算法。在 1993 年，Quinlan 进一步发展了 ID3 算法，改进成 C4.5 算法，成为机器学习的十大算法之一。
ID3 的另一个分支是分类回归决策树算法(Classification Regression Tree)，与 C4.5 不同的是， CART 的决策树主要用于预测，这样决策树理论完整地覆盖了机器学习中分类和回归两个领域了。

基本思想

决策树的思想来源非常朴素，每个人大脑中都有类似 if-then 这样的判断逻辑，其中 if 表示条件， then 就是选择或决策。程序设计中，最基本的语句条件分支结构就是if-then 结构。而最早的决策树就是利用这类结构分隔数据的一种分类学习方法。

例子说明

假定某间 IT 公司销售笔记本电脑产品，为了提高销售收入，公司对各类客户建立了统一的调查表，统计了几个月销售数据之后收集到中的数据，为了提高销售的效率，公司希望通过上表对潜在客户进行分类，并根据上述特征制作简单的销售问卷。以利于销售人员的工作。这就出现两个问题：
- 如何对客户分类？
- 如何根据分类的依据，并给出销售人员指导的意见？

调查表的结果如下

计数	年龄	收入	学生	信誉	是否购
64	青	高	否	良	不买
64	青	高	否	优	不买
128	青	中	否	良	不买
64	青	低	是	良	买
64	青	中	是	优	买
128	中	高	否	良	买
64	中	低	是	优	买
32	中	中	否	优	买
32	中	高	是	良	买
60	老	中	否	良	买
64	老	低	是	良	买
64	老	低	是	优	不买
132	老	中	是	良	买
64	老	中	否	优	不买

现在，将年龄特征等于青年的选项剪切出一张表格，选择第二个特征：收入，并根据收入排序

计数	年龄	收入	学生	信誉	是否购
64	青	高	否	良	不买
64	青	高	否	优	不买
128	青	中	否	良	不买
64	青	中	是	优	买
64	青	低	是	良	买

其中，高收入和低收入的特征值只有一个类别标签买。将其作为叶子节点。然后继续划分中等收入的下一个特征：学生，于是有了下表

计数	年龄	收入	学生	信誉	是否购
128	青	中	否	良	不买
64	青	中	是	优	买

学生特征只有两个取值，当取否时，对应的标签为不买；当取是时，对应的标签为买。此时，学生特征就生成了决策树左侧分支的所有节点。

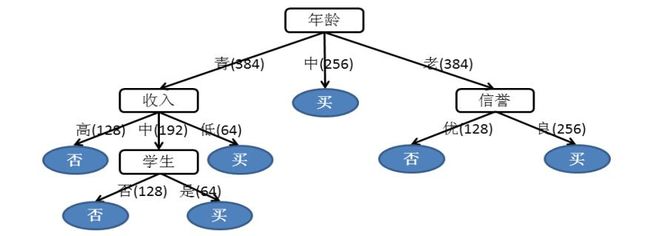
下图中的圆角矩阵为根节点或内部节点：就是可以继续划分的节点；图中的椭圆形节点就是叶子节点，即不能在划分的节点，一般叶子节点都指向一个分类标签，即产生一种决策。

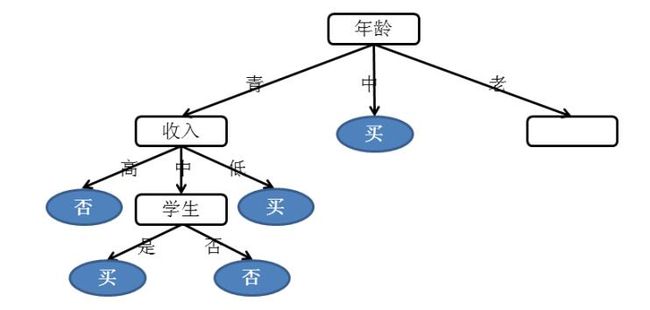
在上面图的基础上，我们再进行如下操作：
- 接下来，我们继续右侧的分支的划分，但在划分时我们做一个简单的变化，划分的顺序为信誉>收入>学生>计数。
这样整个划分过程就变得简单了，当信誉取值为良时，类别标签仅有一个选项就是买。那么信誉为良就是叶子节点。当信誉取值为优时，类别标签仅有一个选项就是不买

• 在展示最终的结果前，再对图做一点调整，为了便于做出判断，我们对这棵树的方向做了调整，即将所有确定购买的叶子节点都放到了树的右侧，不买的节点都放到了树的左侧

• 到目前为止，都是从定性的角度对潜在用户的判断，为了便于从量上进行考量，在图的节点上加上量的标识

最终结果如下

从上面的图，我们得到如下结论
- 如果是中年人，一般会购买本公司的产品；
- 如果是青年人，低收入层都会购买，中等收入层还需要做进一步判断，如果是学生就会购买。
- 如果是老年客户，那么首先看一下他们的信誉，如果是良就会购买，如果信誉为优，多数不会购买。
- 全部的计数特征总数为 1024，将上图中路径边的数据除以 1024 这个总数，就得到了每个节点的购买概率

决策树的执行过程

决策树框架主要包含下面4个部分

决策树主函数

各种决策树的主函数都大同小异，本质上是个递归函数。该函数主要的功能是按照某种规则生长出决策树的各个分支节点，并根据终止条件结束算法。一般来讲，主函数需要完成如下几个功能：
1. 输入需要分类的数据集和类别标签；
2. 根据某种分类规则得到最优的划分特征，并创建特征的划分节点—计算最优特征子函数；
3. 按照该特征的每个取值划分数据集为若干部分—划分数据集子函数；
4. 根据划分子函数的计算结果构建出新的节点，作为树生长出的新分支；
5. 检验是否符合递归的终止条件
6. 将划分的新节点包含的数据集和类别标签作为输入，递归执行上述步骤

计算最优特征子函数

该函数是继主函数外最重要的函数。每种决策树之所以不同一般都因为最优特征选择的标准上有所差异，不同的标准导致不同类型的决策树，例如 ID3 的最优特征选择标准是信息增益、C4.5 是信息增益率，
CART 是节点方差的大小等等。后面所讲的理论部分，都是对特征选择标准而言的。算法逻辑上，一般选择最优特征需要遍历整个数据集，评估每个特征，找到最优的那一个返回。

划分数据集

划分数据集函数的主要功能是分隔数据集，有的需要删除某个特征轴所在的数据列，返回剩余的数据集。有的干脆就将数据集一份为二。
虽然实现有所不同，但基本含义都是一致的。

分类器

所有的机器学习算法要用于分类或回归预测。决策树的分类器就是将测试遍历整个生成的决策树，并找到最终的叶子节点的类别标签。这个标签就是返回的结果。

信息熵测度

虽然我们手工实现了上例的决策过程，但是将这种实现方法使用编程形式自动计算还存在一些问题。首先，特征集中的数据常常表现为定性字符串数据，称为标称数据，使用这些数据的算法缺乏泛化能力，在实际计算中需要将这些数据定量化为数字，也就是所谓的离散化。

我们可以将年龄、收入、学生、信誉这些特征的特征值转换为 0,1,2,…,n的形式。这样，年龄={0（青） ,1（中） ,2（老） }；收入={0（高） ,1（中） ,2（低） }；学生={0（是） ,1（否） }；信誉={0（优） ,1（良） }
完成了特征离散化，回顾一下前面的手工计算过程，我们可以总结出这样一条规律，数据特征的划分过程是一个将数据集从无序变为有序的过程。这样我们就可以处理特征的划分依据问题，即对于一个有多维特征构成的数据集，如何优选出某个特征作为根节点。进一步扩展这个问题，如何每次都选择出特征集中无序度最大的那列特
征作为划分节点。

为了衡量一个事物特征取值的有(无)序程度，下面我们引入一个重要的概念：信息熵。

熵是事物不确定性的度量标准，也称为信息的单位或“测度”。在决策树中它不仅能用来度量类别的不确性，可以来度量包含不同特征的数据样本与类别的不确定性。即某个特征列向量的信息熵越大，就说明该向量的不确定性程度越大，即混乱
程度越大，就应优先考虑从该特征向量着手来进行划分。信息熵为决策树的划分提供最重要的依据和标准。

不同决策树算法的差异，基本都体现在“熵”的计算方法不同，下面对各种算法的计算思路做一个简单的介绍

主要算法以及介绍

ID3算法

ID3 是比较早的机器学习算法，于 1979 年 Quinlan 就提出了算法的思想。它以信息熵为度量标准，划分出决策树特征节点，每次优先选取信息量最多的属性，即使信息熵变为最小的属性，以构造一棵信息熵下降最快的决策树。

但在另一方面， ID3 在使用中也暴露除了一些问题：
- ID3 算法的节点划分度量标准采用的是信息增益，信息增益偏向于选择特征
值个数较多的特征，而取值个数较多的特征并不一定是最优的特征。所以需
要改进选择属性的节点划分度量标准。
- ID3 算法递归过程中依次需要计算每个特征值的，对于大型数据会生成比较
复杂的决策树：层次和分支都很多，而其中某些分支的特征值概率很小，如
果不加忽略就造成了过拟合的问题。即决策树对样本数据的分类精度较高，
但在测试集上，分类的结果受决策树分支的影响很大。

C4.5算法

针对 ID3 算法存在的一些问题， 1993 年， Quinlan 将 ID3 算法改进为 C4.5 算法。该算法成功的解决了 ID3 遇到的诸多问题。在业界得到广泛的应用，并发展成为机器学习的十大算法之一。

C4.5 并没有改变 ID3 的算法逻辑，基本的程序结构仍与 ID3 相同，但在节点的划分标准上做了改进。 C4.5 使用信息增益率（ GainRatio）来替代信息增益（ Gain）进行特征的选择，克服了信息增益选择特征时偏向于特征值个数较多的不足

CART(Classification And Regression Tree)

CART（ Classification And RegressionTree）算法是目前决策树算法中最为成熟的一类算法，应用范围也比较广泛。它既可用于分类，也可用于预测.
西方预测理论一般都是基于回归的， CART 是一种通过决策树方法实现回归的算
法，它有很多其他全局回归算法不具有的特性。
在创建回归模型时， 样本的取值分为观察值和输出值两种，观察值和输出值都是
连续的， 不像分类函数那样有分类标签，只有根据数据集的数据特征来创建一个预测的模型，反应曲线的变化趋势。

在预测中， CART 使用最小剩余方差(Squared Residuals Minimization)来判定回归树的最优划分， 这个准则期望划分之后的子树与样本点的误差方差最小。 这样决策树
将数据集切分成很多子模型数据，然后利用线性回归技术来建模。如果每次切分后的数据子集仍然难以拟合就继续切分。在这种切分方式下，创建出的预测树，每个叶子节点都是一个线性回归模型。 这些线性回归模型反应了样本集合（观测集合）中蕴含的模式，也被称为模型树。因此， CART 不仅支持整体预测，也支持局部模式的预测，并有能力从整体中找到模式，或根据模式组合成一个整体。整体与模式之间的相互结
合，对于预测分析非常有价值。因此 CART 决策树算法在预测中的应用非常广泛。

代码样例

本章节只通过Scikit-Learn 库中的CART实现，来演示如果通过CART来达到预测的效果

# encoding:utf-8
"""CART 的实现有很多种，源码在很多地方都可以找到，相信读者在阅读完前面的
部分之后，有能力看懂，并且实现出 CART 的算法，
这里使用 Scikit-Learn 中的决策树算法来看一下 CART 的预测效果，使读者有一个
直观的认识。"""

__author__ = 'eric.sun'

import matplotlib.pyplot as plt
import numpy as np
from numpy import *
from sklearn.tree import DecisionTreeRegressor

def plotfigure(X,X_test,y,yp):
    plt.figure()
    plt.scatter(X, y, c="k", label="data")
    plt.plot(X_test, yp, c="r", label="max_depth=5", linewidth=2)
    plt.xlabel("data")
    plt.ylabel("target")
    plt.title("Decision Tree Regression")
    plt.legend()
    plt.show()

x = np.linspace(-5,5,200)
print x
siny = np.sin(x) # 给出 y 与 x 的基本关系
X = mat(x).T
y = siny+np.random.rand(1,len(siny))*1.5 # 加入噪声的点集
y = y.tolist()[0]
# Fit regression model
clf = DecisionTreeRegressor(max_depth=4) # max_depth 选取最大的树深度，类似前剪枝
clf.fit(X, y)
# Predict
X_test = np.arange(-5.0, 5.0, 0.05)[:, np.newaxis]
yp = clf.predict(X_test)
plotfigure(X,X_test,y,yp)