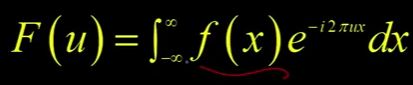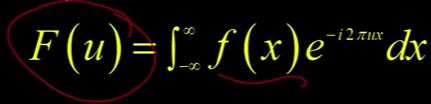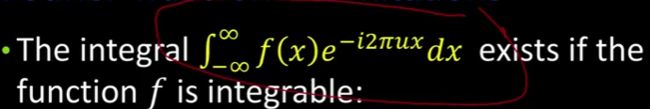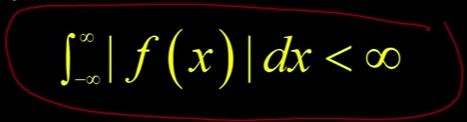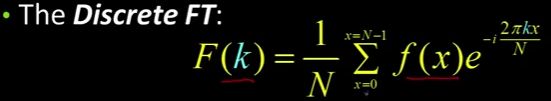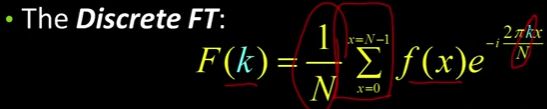10.傅里叶变换——更正式的傅里叶变换，频谱，局限性，离散傅里叶变换_4

目录

更正式的傅里叶变换（Fourier Transform）

频谱（Frequency Spectrum）

局限性

离散傅里叶变换（Discrete Fourier Transform）

---

更正式的傅里叶变换（Fourier Transform）

这样做更正式一点，我们将把信号表示成无穷多个正弦信号的加权和。那么傅里叶变换，在这里，在它美丽的荣耀中，在一维中，Okay。

是傅里叶变换。我们只是对原函数进行无穷积分乘以。你可能会说：什么？减去i......来自哪里？这是怎么来的?

再一次，记得你们可能学过的微积分课，e的ik次方是cosk + isink。

 这就是为什么这是偶数部分，那是奇数部分。这是，

顺便说一下，如果有电气工程师，他们有。 我不知道为什么，因为数学家使用 ，我猜电气工程师不喜欢数学家。我们要一直用  。

傅里叶变换的作用是，它从空间域

转换到频域，

频域是写成，有时像你一样写 ， 就像我们在这里做的那样，有时甚至写成 ，当你讨论损失变换之类的时候。这里的意思是这个大写的F是频谱，或者我应该说它是的频率，但是我们等下会讨论它的大小，我们称这个为频谱。

为了完整性，顺便说一下，这里我们有了傅立叶变换（Fourier Transform）。

这里是逆傅立叶变换（Inverse Fourier Transform），

毫不奇怪，如果你告诉我所有的正弦波是什么，如果我把它们全部加起来，好的，在某个位置X，把所有的正弦信号加起来（du），我就能恢复原始信号。S称为逆傅立叶变换。

频谱（Frequency Spectrum）

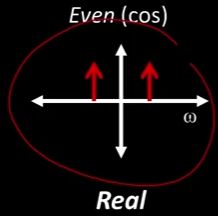
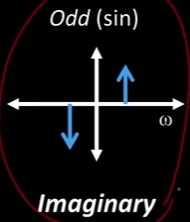
所以把我们刚刚看到的那些方程式放到一些简单的图片中。我们的频率一般可以被认为是从负无穷大到正无穷大。实部是Cosign部分，它的脉冲看起来像这个，

 虚部是奇部，它的Sine部分是这样的，

正如我们之前说过的，通常我们只会担心功率的大小，所以你只需要将正方形的总和搞定就可以了。这就是功率，

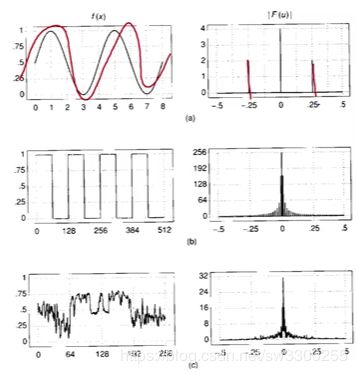
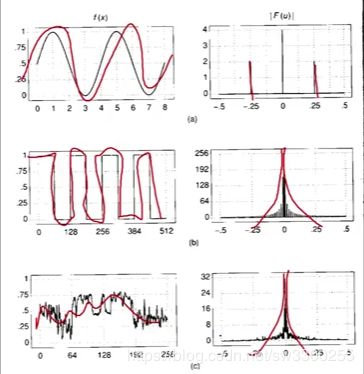
当我把实部和虚部组合成 功率 时，我可以看到不同类型信号的功率谱。这里有一些，我为这张糟糕的图片道歉。这里我们有一个正弦曲线（左图1），我们的正弦曲线只有那里有两个峰值的频率（右图1），对，无论相位如何，根号下的平方和将给我们这两个峰值。

而且在这里我们有那个方波（左图2），你可以看到功率随着频率的增加而减小（右图2）。

这就是我们之前演示的，有趣的是，如果你从某种典型的自然图像中取出信号，或者你带走了一大堆典型的自然信号（左图3），你也会发现这些频谱下降了（右图3），这只是从自然图像的角度来看图像是如何形成的。

局限性

让我们来谈谈这方面的一些限制，这将使我们在一分钟内进入傅里叶级数（Fourier Series）。对于存在的这个积分，这个傅里叶变换，我们实际上并不想要无穷大，对吧？因为这不太好，当我们试着喜欢写下无穷大时，它就要花很长时间。

我们要说的一件事是这整个式子是可积的（如图），

如果原函数本身是可积的（如图），如果我取这个函数，我实际上必须取它的绝对值。如果我把它从负无穷大加到无穷大，它就不会爆炸，它必须被限制为一个值。

你可能会问：“等一下，我认为我们有无穷的循环级数。”我们讲傅里叶级数的时候讲过。我们现在讨论的是傅里叶变换，我们试图使它保持一定的界限。所以这些积分必须存在。它是基于同样的原理，但它的理念，在傅里叶级数（Fourier Series）中，我们讨论过了循环函数。在傅里叶变换（Fourier Transform）中我们讨论的是积分，可积函数。

一分钟后，当我们有一个固定长度的函数，它就很清楚了。事实上，我们现在就来看看（如图）。

你看到它说，显然如果有一个宽度为T的边界。对吧，如果所有的函数都在T范围内，那么显然我可以从- T / 2积分到+ T / 2，对吧? 这就是整个积分。这将引导我们，至少在我扭曲的头脑中，得到离散傅里叶变换（Discrete Fourier Transform）的概念。

离散傅里叶变换（Discrete Fourier Transform）

离散傅里叶变换（Discrete Fourier Transform）是我们想要在计算机中开始工作时必须要做的事情，因为毕竟我们没有连续信号，我们只有离散值。所以离散傅里叶变换就是这样写的。

 现在我们说这里的  是离散频率，对吧?我们要做的是对所有像素求和，

 

所以我们得x来自信号，在这种情况下是，从0到，如果总共有个，

这里是  ，

现在是e的- i次方，看到k / N了吗?

 

因为基本上，我们不把频率看作是它在时间上摆动的速度，而是在图像的整个长度上摆动的速度。所以，k被写成，它是信号每一周期的周期数，或者图像每一周期的周期数，对吧?  Cycles per image. 这只有从0到N / 2才有意义。为什么只有N / 2？

好吧，想想正弦曲线在N个像素的图像中摆动的速度有多快，对吧？它会变成白色，一直到黑色，一直到白色，一直到黑色......所以周期是2。所以频率，循环次数，应该是N / 2。基本上，k只能从 -N / 2到 +N / 2，因为这是你在离散图像中可以拥有的最高频率。

---

——学会编写自己的代码，才能练出真功夫。