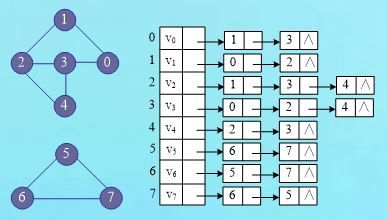
数据结构例程——非连通图的遍历

本文是[数据结构基础系列(7)：图]中第7课时[非连通图的遍历]的例程。

（程序中graph.h是图存储结构的“算法库”中的头文件，详情请单击链接…）

1、非连通图的深度优先遍历——DFS

#include 
#include 
#include "graph.h"
int visited[MAXV];     //定义存放节点的访问标志的全局数组
void DFS(ALGraph *G, int v)
{
    ArcNode *p;
    int w;
    visited[v]=1;
    printf("%d ", v);
    p=G->adjlist[v].firstarc;
    while (p!=NULL)
    {
        w=p->adjvex;
        if (visited[w]==0)
            DFS(G,w);
        p=p->nextarc;
    }
}

//采用深度优先搜索遍历非连通无向图
void DFS1(ALGraph *G)
{
    int i;
    for (i=0; in; i++)
        if (visited[i]==0)
            DFS(G,i);
}

int main()
{
    int i;
    ALGraph *G;
    int A[8][8]=
    {
        {0,1,0,1,0,0,0,0},
        {1,0,1,0,0,0,0,0},
        {0,1,0,1,1,0,0,0},
        {1,0,1,0,1,0,0,0},
        {0,0,1,1,0,0,0,0},
        {0,0,0,0,0,0,1,0},
        {0,0,0,0,0,1,0,1},
        {0,0,0,0,0,0,1,0},
    };
    ArrayToList(A[0], 8, G);
    for (i=0; in; i++)
        visited[i]=0; //访问标志数组初始化
    printf(" 非连通图的广度优先遍历:\n");
    DFS1(G);
    return 0;
}

2、非连通图的广度优先遍历——BFS

#include 
#include 
#include "graph.h"
int visited[MAXV];     //定义存放节点的访问标志的全局数组
void BFS(ALGraph *G, int v)
{
    ArcNode *p;
    int w;
    int queue[MAXV],front=0,rear=0; //定义循环队列
    printf("%2d",v);            //输出被访问顶点的编号
    visited[v]=1;                       //置已访问标记
    rear=(rear+1)%MAXV;
    queue[rear]=v;              //v进队
    while (front!=rear)         //若队列不空时循环
    {
        front=(front+1)%MAXV;
        w=queue[front];             //出队并赋给w
        p=G->adjlist[w].firstarc;   //找w的第一个的邻接点
        while (p!=NULL)
        {
            if (visited[p->adjvex]==0)
            {
                printf("%2d",p->adjvex); //访问之
                visited[p->adjvex]=1;
                rear=(rear+1)%MAXV; //该顶点进队
                queue[rear]=p->adjvex;
            }
            p=p->nextarc;       //找下一个邻接顶点
        }
    }
    printf("\n");
}

//采用广度优先搜索遍历非连通无向图
void BFS1(ALGraph *G)
{
   int i;
   for (i=0;in;i++)
      if (visited[i]==0)
           BFS(G,i);
}

int main()
{
    int i;
    ALGraph *G;
    int A[8][8]=
    {
        {0,1,0,1,0,0,0,0},
        {1,0,1,0,0,0,0,0},
        {0,1,0,1,1,0,0,0},
        {1,0,1,0,1,0,0,0},
        {0,0,1,1,0,0,0,0},
        {0,0,0,0,0,0,1,0},
        {0,0,0,0,0,1,0,1},
        {0,0,0,0,0,0,1,0},
    };
    ArrayToList(A[0], 8, G);
    for (i=0; in; i++)
        visited[i]=0; //访问标志数组初始化
    printf(" 非连通图的广度优先遍历:\n");
    BFS1(G);
    return 0;
}

3、判断连通图

#include 
#include 
#include "graph.h"
int visited[MAXV];     //定义存放节点的访问标志的全局数组
void DFS(ALGraph *G, int v)
{
    ArcNode *p;
    int w;
    visited[v]=1;  //此处做了标记即完成了访问，不必下句的输出
    //printf("%d ", v);
    p=G->adjlist[v].firstarc;
    while (p!=NULL)
    {
        w=p->adjvex;
        if (visited[w]==0)
            DFS(G,w);
        p=p->nextarc;
    }
}

//是连通图返回true，否则返回false
bool Connect(ALGraph *G)
{
    int i;
    bool flag=true;
    for (i=0; in; i++)
        visited[i]=0;
    DFS(G,0);
    for (i=0; in; i++)
        if (visited[i]==0)
        {
            flag=false;
            break;
        }
    return flag;
}

int main()
{
    int i;
    ALGraph *G;
    int A[8][8]=
    {
        {0,1,0,1,0,0,0,0},
        {1,0,1,0,0,0,0,0},
        {0,1,0,1,1,0,0,0},
        {1,0,1,0,1,0,0,0},
        {0,0,1,1,0,0,0,0},
        {0,0,0,0,0,0,1,0},
        {0,0,0,0,0,1,0,1},
        {0,0,0,0,0,0,1,0},
    };
    ArrayToList(A[0], 8, G);
    for (i=0; in; i++)
        visited[i]=0; //访问标志数组初始化
    if(Connect(G))
        printf(" G是连通图\n");
    else
        printf(" G不是连通图\n");
    return 0;
}

附：测试用的图及存储结构