CSS-Tree的原理与实现

　　最近在捣腾OpenCL实现两个数据库表的连接操作。我参考的论文里面讲到，在实现INLJ（带索引的嵌套循环连接）以及SMJ（排序合并连接）上作者使用了CSS-Trees进行优化。我之前对这方面不怎么了解，所以花了一个晚上的时间找到了他们参照的讲述CSS树的论文，自己稍微研究了一下，有些心得与收获。希望能借此记录下来，供自己以后翻看。

　　CSS树(Cache-Sensitive Search Trees)是一种缓存敏感的主存数据库索引。由于现在计算机硬件技术发展迅猛，计算机的内存都在GB级以上。这对主存数据库（简单地说，即整个数据库的数据都存放在内存中，而不是磁盘中）的实现提供了重要支持。相比较传统的基于磁盘阵列的数据库，主存数据库在性能上并不再需要考虑磁盘I/O的时间问题。但同时，新的问题也出现了。我们都知道CPU访问内存的机制，它并不是直接访问内存的，而是先在高速缓存中搜索，当缓存中存在需要的数据时(cache hit)则直接将数据传送至CPU；当缓存中不存在需要的数据(cache miss)则再访问内存，将内存中需要的那一块数据写到缓存中，并读取到CPU中。当然，CPU读取缓存的时间比读取内存的时间要短得多。而主存数据库在数据读取十分频繁的场景中，其直接命中缓存的几率将直接影响其性能。这也是缓存敏感技术的发现缘由。缓存敏感，即尽量考虑缓存中存在的数据，保证它们能频繁地被访问，同时能够减少CPU访问内存的次数。所以一般主存数据库的索引就是存入缓存内容的最佳选择。

　　在一个对于某属性是有序的数据库表中查询满足该属性条件的条目，方法有许多：从最简单的顺序查找、二分查找，到T-Trees, B+-Trees等。但并不是每种方法都能考虑到缓存的问题。Jun Rao 和 Kenneth A. Ross在1998年的论文"Cache Conscious Indexing for Decision-Support in Main Memory"中对这些数据结构在主存数据库中存在的合理性进行了分析。（这篇博文也是参照这篇论文写的）我就在此稍微概括一下：

　　Array Binary Search (数组二分搜索)：由于二分搜索在每次循环中当前的mid值都不同（mid = (begin + end)/2 ），每次搜索空间时都会缩短一半的长度，那么mid值变化也会非常大。造成的结果就是：每次访问arr[mid]（arr是一个数组）都会造成cache miss。最糟糕的情况就是，每次做比较之前读取数据的时候都会出现cache miss。如此，效率是非常低的。

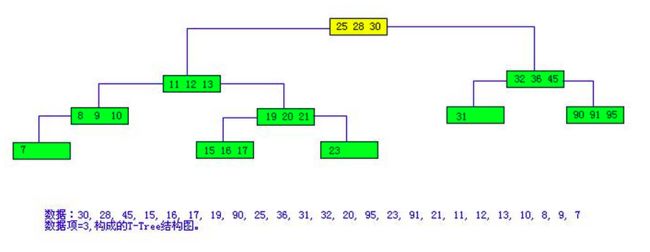
　　T-Trees（T树）：说实话我之前也不知道T树是个什么东西。我在网上找到了一个图，一看就明白了：

图呃...0吧：T-Tree

　　看上去T树中的所有节点都储存了数据。Rao et al.在论文中提到，虽然T树将数据存在了树节点上，这样看似是缓存敏感的，但是实际上很多情况下只有一个节点的头尾会被访问到（访问头尾即需要的数据并不在本节点中），这样缓存的利用率其实是很低的。因为进行key的比较次数和二分搜索是一样的，故T树并不能得到比二分搜索更好的性能。

　　B+-Trees（B+树）：在磁盘数据库系统中，B+树是使用得最广泛的索引技术。其目的在于减少数据磁盘I/O的次数。这是通过传入索引所在的磁盘页并对其进行检索后得到确切的条目所在的页数再进行读写来实现的。这次要讲到的CSS树基本上也是基于这种思想。Rao说B+树比T树在缓存上有更好的表现。但是B+树在节点中需要储存指向孩子节点的指针。这些指针占用了一定的空间，使得整个B+树索引有用的信息所占的比例不高。CSS数则是通过数组下标的计算来获得子节点，故省去了存储子节点指针的空间。

　　Hash（哈希）：哈希索引的使用也十分广泛。哈希索引中存在一个链式哈希桶，每个桶里面装有指向具有某个哈希值的所有条目的数组。显然，哈希索引的这种组织形式也是可以做到缓存敏感的。但是哈希索引需要的空间非常大，在处理不均匀的数据表时性能一般（即某些桶的数组长度非常大）。同时，哈希索引并没有从数据表的有序性中获得什么好处。

　　OK，废话了这么多，现在来讲讲CSS树吧。不过需要说的一点是：CSS树在对数据的插入、删除操作比较少，而查询操作比较多的情况下表现优异。因为每次插入新数据都要重新构建一棵CSS树。构建的时间也不长，但是已经明显长于查询的时间了，后面可以看到。我在数据库连接操作的并行算法中使用到CSS树是因为我需要在一个存于global memory中的数据表进行检索与匹配。每个线程都需要二分访问数据表。但是如果将CSS树存于local memory中，那么最后可能只需要访问1-2次global memory就能找到条目了。（访问local memory的时间比访问global memory短了几十倍）当然如果需要同时兼顾到添加删除的效率，可以读读Rao Jun他们写的另外的论文，例如他们提出的CSB+树，这里就不赘述了。

　　总的来说，CSS树的实现思路非常简单：根据已有的有序数据a，生成一个索引数组b。这个数组b表示一棵完全m+1叉树（就像完全二叉树可以用一维数组来存储），m是每个非叶子节点中索引项的个数。m个索引项自然就产生了m+1个间隙（包括两边）。一棵CSS树的示意图如图1所示：

图1：长度为65*4的数组生成的CSS-Tree

　　其中，0-15号节点被称为内部节点(internal node)，存放的是索引项，而16-80号节点是叶节点，存放的是实际的数据（即数组a中的数据）。所以我们可以看到，每个节点都是有编号的，而每个内部节点拥有m个索引项，每个叶节点则拥有m个数据项。确定了m后，我们可以以此计算编号为n的节点的子节点编号（如果存在的话）以及该子节点拥有的索引项在索引数组b中的index。以上图为例，这样的CSS树显然能存储的有效数据（数组a）的大小是(80-16+1)*4 = 260个。

　　这个图是从上面提到的那篇论文中截下来的，图很抽象，当然这篇论文的表述本来就略显晦涩。里面提到了各种index的计算，但是有些比较关键的地方没有讲，所以我花了不少劲才读懂这篇论文的想法。这里为了方便读者，我还是用图2来讲述吧：

图2：长度为30的数组a生成的CSS-Tree

　　本例子中，m=2，黑色数字代表节点编号，红色数字代表实际的数据项，蓝色数字代表索引项，紫色字符串是表示索引项在索引数组中的位置。

　　CSS树中比较tricky的地方就是实际存储数据的节点顺序关系（图中7-12号节点，以及13-21号节点）。13-21号节点的节点标号大，但是里面存储的却是数组a前面的元素，7-12号则是反过来的。引用论文里的一张图如下图3，即 I 和 II 两部分是反过来的。

图3：65*4长度数组与索引后的数组对应关系

　　对于图2，我们姑且把节点13-21的部分（较深的叶节点）称为Part 1， 7-12的部分（较浅的叶节点）称为Part 2吧。那么搜索的时候，当我们算到目标位于Part1的时候，就应该在数组的前面部分寻找；算到目标位于Part 2 的时候，就应该在数组的后面部分寻找。具体寻找的思路后面会细说。

　　注意：接下来的部分都以图2的长度为30个数组CSS-Tree构建为描述的目标。

　　针对这样的CSS树，有几个关键的数字需要先算一下，后面的构建与查询函数中都将用到这几个数字。假设有效数组a长度为total，m=2：

　　1）B值，中间结果，方便后面的运算，公式： （原谅我不会在csdn中插入公式......）

　　2） k值：中间结果，方便后面的运算，公式：。

　　3）内部节点个数 numOfInternalNodes：即图2中存有蓝色数字的节点的数量（6个），公式是。

　　4） 最底层的第一个叶子节点的编号 leftMostLeaveNo ：即图2中的节点13 ，公式是。

　　算好这些数字后，我们就开搞吧。

1. CSS-Tree的构建

　　CSS树的构建跟一般的二叉搜索树构建方法差不多。主要思想就是：每个索引项的值都是该索引项的左子树中数据项的最大值。用一个循环在左子树中不断获取最右的孩子，达到叶子节点时，最右的孩子即为最大值了。索引树的构建顺序，从最后一个索引项开始往前构建，一直到根节点为止。最后一个索引项位于最后一个内部节点中，这也是我们为什么一开始需要计算内部节点个数numOfInternalNodes。很容易得到，最后一个内部节点编号lNode = numOfInternalNodes - 1.

　　了解CSS树的构建思想后，这里贴上论文中的伪代码，针对伪代码进行一些必要的解释，并在后面附上自己写的源代码。

　　伪代码：　　

Input: the sorted array (a),
	number of elements in the array (n).
Output: the array storing the internal nodes of a full CSS-tree (b).
	last internal node number (lNode).
	index of the first entry of the leftmost leaf node in the bottom level in a CSS directory array. (MARK).
Method:
Calculate the number of internal nodes needed and allocate space for b. Calculate lNode, MARK.
for i=the array index of the last entry of node lNode to 0 {
	Let d be the node number of entry i.
	Let c be the node number of entry i’s immediate left child node.
	while (c <= lNode) {
		Let c be the node number of the (m+1)th child of c.
	}
	//now we are at the leaves, map to the sorted array.
	Let diff be the difference of the array index of the first entry in node c and MARK.
	if (diff<0) { //map to the second half of the array from the end.
		b[i]=a[diff+n+m-1]; 
	}
	else { //map to the first half of the array from the beginning. 
		if ((diff+m-1) is in the first part of the array)
			b[i]=a[diff+m-1]; 
		else
			b[i]=the last element in the first part of the array. 
	}
}
return b, lNode and MARK.

　　算法的输出有三项：索引数组b，最后一个内部节点编号lNode，以及最左叶节点的最左的数据项在索引数组中的位置。最后这句话有些难懂，可以参考图3中节点31的位置。它所拥有的数据项应该是有序数组a的第0到3项，但是在上面的directory in an array中，节点31是排在了后面的，它的数据项的编号应该是125(31 * 4 + 1)到128(31 * 4 + 3)。这个数据（称为MARK）的作用是为了在后面访问数据项的时候确定该数据项是属于Part 1 还是 Part 2. (可以看到后面计算diff的时候用到了MARK)

　　while循环做的事情就是找到左子树的最大数据项所在的节点编号。后面的if语句则是然后计算这个节点中的数据项属于哪个Part。最后的else里面分了两种情况，即diff + m - 1是否属于Part 1. 这是为了应对一些异常情况的，后面会讲到。因此，我们还需要计算Part 1 最后一个元素的位置。

　　以下是我根据这份伪代码写出来的源代码。源代码中写了许多注释，注释针对的是图2的情况：

//在我们的case中，total = 30, m = 2
int* generateCSSTree(int *a, int total, int m, int &numOfInternalNodes, int &mark) {
    
    int B = ceil(1.0 * total / m );								//B = 15
    int k = ceil(log(B)/log(m+1));								//k = 3
    numOfInternalNodes = (pow(m+1, k) - 1)/m - floor((pow(m+1, k) - B)/m) ;     		//内部节点个数（7）
    int leftMostLeaveNo = (pow(m+1, k) - 1)/m;                 					//最左叶节点编号（13）
    int lastEleInPartOneIdx = total - ( leftMostLeaveNo - numOfInternalNodes ) * m - 1 ;   //计算Part 1的最后一个元素编号(17)，元素为28
    
    int *b = new int[numOfInternalNodes * m];     					   //索引数组b长度为numOfInternalNodes * m
    
    int lNode = numOfInternalNodes - 1;     							// lNode = 6，最后一个内部节点编号
    mark = leftMostLeaveNo * m ;     								//mark = 13 * 2  = 26

    for(int i = numOfInternalNodes * m - 1; i >= 0; i--) {
        int d = i/m;										//获取索引项i所在的节点编号d
        int c = d * (m + 1) + 1 + i % m;							//c为索引项i的左子树根节点编号
        while (c <= lNode) {
            c = c * ( m + 1 ) + m + 1;								//搜索最右子树
        }
        //此时c到达叶节点
        int diff = c * m  - mark;		//mark = 26							
        
        if (diff < 0) {     	//对应Part 2 
            b[i] = a[diff + total + m - 1];	//叶子节点最大的数据项（最右孩子）
        }
        else {              	//对应Part 1
            if (diff + m - 1 <= lastEleInPartOneIdx)		//叶子节点最右孩子不为空
                b[i] = a[diff + m - 1];		//叶子节点最大数据项
            else
                b[i] = a[lastEleInPartOneIdx];			//叶子节点最右孩子为空，用Part 1的最大元素补全
        }
    }
    return  b;
}

　　刚读伪代码的时候，我不是很懂为什么最后需要判断叶子节点的最右节点是否为空。我以为最右节点一直是存在的。于是我画了下面的一幅图：

图4：可能出现的情况

　　代码中diff + m - 1找到的是节点11的最右孩子，但是它是空的，所以在这种情况下我们就需要用50来填充b[7]。

2. CSS-Tree的搜索

　　搜索的方法和一般的二叉搜索类似。主要思想是：在每个树的内部节点中对节点里面的索引项二分查找，找到接下来应该去的branch，然后一路照下来，到叶子节点时，再使用二分查找看叶子节点中是否存在该数据即可。注意，当出现数据重复的现象时，CSS树能保证找到的index是leftmost的。

　　伪代码：

Input:    the sorted array (a),
	  the array consisting of the internal nodes of a full CSS-tree (b).
	  number of elements in the sorted array (n).
	  last internal node number (lNode).
	  index of the first entry of the leftmost leaf node in the bottom level in a CSS directory array. (MARK).

Output:   the index of the matching key in array a: if the key is found; 
 	  -1: otherwise.

Method:
d=0;
while (d <= lNode) {
	binary search node d to find the correct branch l to go to. (hard-coded)
	Let d be the node number of the lth child of d. 
}

Let diff be the difference of the array index of the first entry in node d and MARK.

if (diff<0) { //map to the second half of the array from the end.
	binary search a[num+diff..num+diff+m-1]. (hard-coded) 
}
else { //map to the first half of the array from the beginning. 
	binary search a[diff..diff+m-1]. (hard-coded)
}
if (the last binary search succeeds)
	return the index of the matching key in array a;
else
	return -1;

　　这里应该就不需要太多解释了。稍微注意一下的就是在非叶子节点和叶子节点中二分搜索的策略是不一样的：假设我们需要的数据为obj。在非叶子节点中，不需要判断obj是否存在于索引项中，只需要根据索引项判断我们需要走向哪个branch；在叶子节点中，我们才需要判断obj是否存在。

　　下面直接上源代码：

int bisearchInNode(int *input, int begin, int end, int obj);		//非叶子节点中的二分搜索
int bisearch(int *input, int begin, int end, int obj);			//叶子节点中的二分搜索

int searchInCSSTree(int obj, int *a, int *b, int num, int m, int numOfInternalNodes, int mark)
{
    int res = -1;
    
    int d = 0;
    while (d <= numOfInternalNodes - 1) {
        int first = d * m;
        int last = d * m + m - 1;
        int nextBr = bisearchInNode(b, first, last, obj);
        if (nextBr != -1)					
            d = d * (m + 1) + 1 + nextBr - first;
        else						//nextBr = -1说明应走向节点最右边的branch
            d = d * (m + 1) + m + 1;
    }
    
    int diff = d * m  - mark;
    
    if (diff < 0) {  //数据项在Part 2 中
        res = bisearch(a, num + diff, num + diff + m - 1, obj);
    }
    else {  //数据项在Part 1中
        res = bisearch(a, diff, diff + m - 1, obj);
    }
    
    return  res;
}

　　两个二分搜索代码：

int bisearch(int *input, int begin, int end, int obj) {          
    int res = -1;
    int mid;
    
    while (begin <= end) {
        mid = (begin + end)/2;
        if (obj > input[mid])   begin = mid+1;
        else {
            if (obj == input[mid])  res = mid;
            end = mid-1;
        }
    }
    return res;
}

int bisearchInNode(int *input, int begin, int end, int obj) {          
    int res = -1;
    int mid;
    
    while (begin <= end) {
        mid = (begin + end)/2;
        if (obj > input[mid])   begin = mid+1;
        else {
            res = mid;
            end = mid-1;
        }
    }
    return res;
}

　　最后还有一点关于 Level CSS-Trees的。在我们前面的实现中，m的取值一直没有什么讲究。例如，当m取8的时候，在非叶子节点中的二分搜索是下面这样的：

图5：m=8时的二分搜索情况

　　当m为8时，一个节点会有9个branch。其中的7个需要比较3次，而2个需要4次。为了使得每个branch都比较一样多的次数，建议当m = 2^k时，只使用其中的m-1个存储索引。这样的实现就叫作Level CSS-Trees. 这次这般，在节点中搜索的时间可以稍微减少一些，但是存储索引的空间增大了（因为每个节点中有一个项空着）。在这里就不赘述了，有兴趣的读者可以读读这篇论文。

　　[参考文献]：Rao, Jun, and Kenneth A. Ross. "Cache conscious indexing for decision-support in main memory." (1998).