聚类算法_层次聚类_密度聚类(dbscan,meanshift)_划分聚类(Kmeans)详解
注: 两整天的成果,谬误之处勿喷
1 聚类概述
样本
- 没有训练的样本
- 没有标注的样本
1.1 相似度度量
1.1.1 距离相似度度量
- 距离度量 d i s t ( o i , o j ) dist(o_{i},o_{j}) dist(oi,oj)
- 欧式距离
- 距离相似度度量
s i m ( o i , o j ) = 1 1 + d i s t ( o i , o j ) sim(o_{i},o_{j})= \frac{1}{1+dist(o_{i},o_{j})} sim(oi,oj)=1+dist(oi,oj)1
1.1.2 密度相似性
- 体现的内涵:
- (1)数据结构特性
- (2)数据结构特性相似
- 密度: 单位空间内对象的个数
- 密度相似度定义: 设 c i , c j 点 的 密 度 为 d i , d j c_{i},c_{j}点的密度为d_{i},d_{j} ci,cj点的密度为di,dj
d e n s i t y ( c i , c j ) = ∣ d i − d j ∣ density(c_{i},c_{j})=|d_{i}-d_{j}| density(ci,cj)=∣di−dj∣
1.1.3 连通相似性
- 定义:
- 数据集用图表示, 节点是对象,边线是关系
- 簇定义为图的连接分支
1.1.4 概念相似性独立
- 语义的相似性
1.2 质量评价指标
- 内部质量评价标准
- CH指标
- 簇间距离和簇内距离的比值
- CH指标值越大 效果越高
- CH指标
- 外部质量评价标准
- 纯度:取值范围小于1,越大越好
1.3 常用的聚类方法
1.3.1 按照聚类的度量
- 基于距离的聚类算法
- 基于密度的聚类算法
- 基于互连性的聚类算法
1.3.2 基于分析方法的思路
- 划分法:
- 层次法:
- 密度法:
- 网格法
- 模型法
2 层次聚类算法
2.1 层次聚类算法概述
- 自顶向下:divisive
- 自底向上:agglomerrative
- 可以用树状图或者嵌套图表示
- 类间距离度量:
- 最短距离:最大相似度
- 最长距离:最小相似度
- 平均距离
- 中心点距离
2.2 diana算法
2.2.1 diana算法简介
自顶向下分裂
- 输入: 包含n个点(对象)的数据集,簇的数目k。
- 输出: k个簇,达到终止条件规定簇数目
度量方法
- 簇的直径:在一个簇中的任意两个数据点的距离中的最大值
- 平均相异度(平均距离)
将所有对象整个当成一个初始簇;
将splinter group和old party两个对象集合置为空;
for (i=1; i≠k; i++)
{ 在所有簇中挑出具有最大直径的簇C;
找出C中与其他点平均相异度最大的一个点p;【离群点】
把p放入splinter group,剩余的点放在old party中;
do【离群点的吸引力】
{ 在old party里找出到splinter group中点的最近距离不大于到old party
中点的最近距离的点;
将该点加入splinter group;
} until (没有新的old party的点被分配给splinter group);
splinter group和old party为被选中的簇分裂成的两个簇,与其他簇一起
组成新的簇集合;
}
2.2 agnes算法
2.2.1 agnes算法简介
自底向上凝聚
输入: 包含n个点(对象)的数据集,簇的数目k。
输出: k个簇,达到终止条件规定簇数目。
方法: 其过程描述如下:
将每个点当成一个初始簇;
do
{ 根据两个簇中最近的数据点找到最近的两个簇;
合并两个簇,生成新的簇的集合;
} until (达到定义的簇的数目);
2.3 算法优缺点总结
- 简单,理解容易
- 合并点/分裂点选择不太容易
- 合并/分类的操作不能进行撤销
- 大数据集不太适合
- 执行效率较低O(t*n2), t为迭代次数, n为样本点数。
3 划分法
指定的聚类的数目和目标,通过反复迭代来进行优化
3.1 K-均值
对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大
3.3.1 K-均值聚类步骤
- 1.随机的选取K个中心点,代表K个类别;
- 2.计算N个样本点和K个中心点之间的欧氏距离;
- 3.将每个样本点划分到最近的(欧氏距离最小的)中心点类别中——迭代1;
- 4.计算每个类别中样本点的均值,得到K个均值,将K个均值作为新的中心点——迭代2;
- 5.重复步骤2、3、4;
- 6.满足收敛条件后,得到收敛后的K个中心点(中心点不再变化)
3.1.2 K值的选择
注:引用自易学智能
- 可视化数据,通过观察数据的聚合程度判断K值
K ≈ sqrt(N/2)- 拐点法:把聚类结果的F-test值(类间Variance和全局Variance的比值)对聚类个数的曲线画出来,选择图中拐点
- Silhouette法
- 交叉验证
- 核方法:构造Kernal矩阵,对其做eigenvalue decomposition,通过结果统计Compactness,获得Compactness—K曲线,选择拐点
3.1.3 代码实现
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=300, centers=4,
cluster_std=0.60, random_state=0)
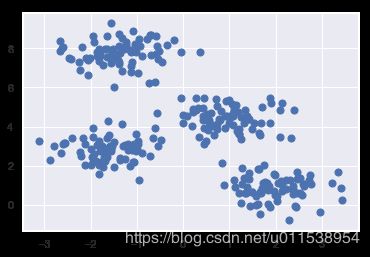
plt.scatter(X[:, 0], X[:, 1], s=50);
from sklearn.cluster import KMeans
"""
KMeans(n_clusters=8, init='k-means++', n_init=10, max_iter=300,
tol=0.0001, precompute_distances='auto', verbose=0,
random_state=None, copy_x=True, n_jobs=1, algorithm='auto')
Parameters:
n_clusters: 聚类个数
max_iter: 最大迭代数
n_init: 用不同的质心初始化值运行算法的次数
init: 初始化质心的方法
precompute_distances:预计算距离
tol: 关于收敛的参数
n_jobs: 计算的进程数
random_state: 随机种子
copy_x:是否修改原始数据
algorithm:“auto”, “full” or “elkan”
”full”就是我们传统的K-Means算法,
“elkan”elkan K-Means算法。默认的
”auto”则会根据数据值是否是稀疏的,来决定如何选择”full”和“elkan”,稠密的选 “elkan”,否则就是”full”
Attributes:
cluster_centers_:质心坐标
Labels_: 每个点的分类
inertia_:每个点到其簇的质心的距离之和。
"""
m_kmeans = KMeans(n_clusters=4)
质心位置:KMeans.cluster_centers_
from sklearn import metrics
def draw(m_kmeans,X,y_pred,n_clusters):
centers = m_kmeans.cluster_centers_
print(centers)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=50, cmap='viridis')
#中心点(质心)用红色标出
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.5)
print("Calinski-Harabasz score:%lf"%metrics.calinski_harabaz_score(X, y_pred) )
plt.title("K-Means (clusters = %d)"%n_clusters,fontsize=20)
m_kmeans.fit(X)
KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
n_clusters=4, n_init=10, n_jobs=None, precompute_distances='auto',
random_state=None, tol=0.0001, verbose=0)
y_pred = m_kmeans.predict(X)
draw(m_kmeans,X,y_pred,4)
[[-1.37324398 7.75368871]
[ 1.98258281 0.86771314]
[-1.58438467 2.83081263]
[ 0.94973532 4.41906906]]
Calinski-Harabasz score:1210.089914
3.2 K-Means++
为了初始值足够离散,我们选择相距较远的点成为质心
3.2.1 K-Means++聚类步骤
-
- 首先在数据集中,随机选取一点,作为第一个质心。
-
- 然后迭代所有点,把所有点到该簇中心的最短距离算出(当有n个质心时,最短距离取n个距离的最小值)
-
- 选取距离较大的点作为新的质心
-
- 重复2和3直到选择出K个质心
-
- 用这k个质心作为初始化质心去运行标准的K-Means算法
3.2.2 代码实现
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
import pylab
pylab.rcParams['figure.figsize'] = (15.0, 8.0)
# X 创建300个随机坐标,范围是[-6,6]
X=(np.random.rand(300,2)*12)-6
# Y 创建300个随机坐标,范围是[0,1]
y=np.random.randint(0,2,size=(300,1))
#plt.scatter(X[:, 0], X[:, 1], s=50);
3.2.2.1 k-means实现
from sklearn.cluster import KMeans
from sklearn import metrics
# 分3个质心,初始质心方法为随机,随机数种子为0
kmeans = KMeans(n_clusters=3,init='random',random_state=0)
kmeans.fit(X)
y_pred = kmeans.predict(X)
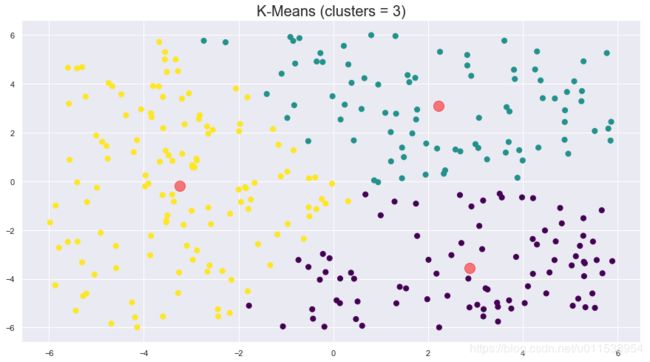
draw(kmeans,X,y_pred,3)
print("迭代次数:%d"%kmeans.n_iter_)
[[ 2.87269719 -3.55992419]
[ 2.21813913 3.08729214]
[-3.23580435 -0.18981553]]
Calinski-Harabasz score:248.378372
迭代次数:8
3.2.2.2 k-means++实现
# 分3个质心,初始质心方法为K-Means++
kmeans = KMeans(n_clusters=3,init='k-means++')
kmeans.fit(X)
y_pred = kmeans.predict(X)
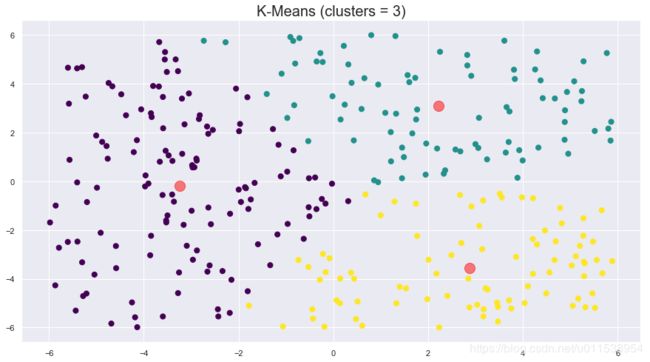
draw(kmeans,X,y_pred,3)
print("迭代次数:%d"%kmeans.n_iter_)
# 质心坐标
# print(kmeans.cluster_centers_)
[[-3.23580435 -0.18981553]
[ 2.21813913 3.08729214]
[ 2.87269719 -3.55992419]]
Calinski-Harabasz score:248.378372
迭代次数:18
4 密度聚类
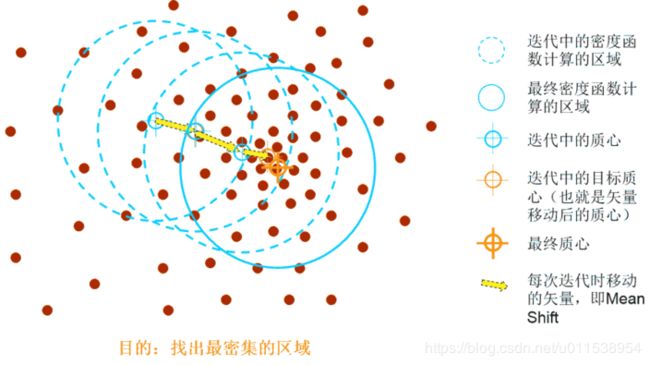
4.1 Mean Shift算法
4.1.1 算法原理
4.1.1.1 例子
像一群具有挑战精神的登山者去攀爬一座山脉,山脉有着很多个山峰,而登山者随机分布在山脉的任何地方,登山者会选择最该块区域最陡峭的方向进行攀爬,直到所有的登山者都爬上了邻近的山峰(局部最优点),山峰的个数也就是簇的个数,这就是Mean Shift算法的基本思想。
4.1.1.2 算法概念
Mean Shift算法是一种无参密度估计算法或称核密度估计算法,
可用于聚类、图像分割、跟踪等,Mean shift是一个向量,它的方向指向当前点上概率密度梯度的方向。
所谓的核密度评估算法,指的是根据数据概率密度不断移动其均值质心(也就是算法的名称Mean Shift的含义)直到满足一定条件。
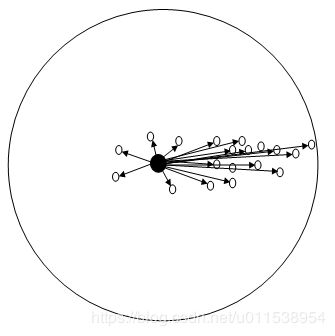
其中,Sh(x)指的是一个半径为h的高维球区域,如上图中的圆形区域。Sh(x)的定义为:
S h ( x ) = ( y ∣ ( y − x ) ( y − x ) T ⩽ h 2 ) S_h(x)=(y \mid (y-x)( y-x)^T \leqslant h^2) Sh(x)=(y∣(y−x)(y−x)T⩽h2)
里面所有点与圆心为起点形成的向量相加的结果就是Mean shift向量。
4.1.1.3 算法步骤
- (1)在未被标记的数据点中随机n个点作为n个聚类的起始中心点center
- (2)找出以center为中心,半径为radius的区域中出现的所有数据点,认为这些点同属于一个聚类C。同时将在该聚类中数据点的访问频率加1。
- (3)以center为中心点,计算center点到集合M中每个数据点的向量之和,得到向量shift。
注: Mean Shift向量
对于给定的d维空间 R d R^d Rd 中的n个样本点 x i , i = 1 , ⋯ , n x_i,i=1,⋯,n xi,i=1,⋯,n
则对于点x,其Mean Shift向量的基本形式为:
M h ( x ) = 1 k ∑ x i ∈ S h ( x i − x ) M_h(x)=\frac{1}{k}\sum_{x_i\in S_h}(x_i-x) Mh(x)=k1xi∈Sh∑(xi−x)
-
(4) center点沿着shift的方向移动,移动距离是||shift||, 符号表达式为: center = center + shift。
-
(5) 迭代: 重复步骤2、3、4,直到shift的很小(就是迭代到收敛),记住此时的center。注意,这个迭代过程中遇到的点都应该归类到簇C
-
(6) 如果收敛时当前簇C的center与其它已经存在的簇C2中心的距离小于阈值,那么把C2和C合并,数据点出现次数也对应合并。否则,把C作为新的聚类。
-
(7)重复1、2、3、4、5直到所有的点都被标记为已访问。
-
(8)分类:根据每个类,对每个点的访问频率,取访问频率最大的那个类,作为当前点集的所属类。
4.1.2 代码实现
import numpy as np
import pandas as pd
import pylab
pylab.rcParams['figure.figsize'] = (15.0, 8.0)
# X 创建300个随机坐标,范围是[-6,6]
X=(np.random.rand(300,2)*12)-6
# Y 创建300个随机坐标,范围是[0,1]
y=np.random.randint(0,2,size=(300,1))
#plt.scatter(X[:, 0], X[:, 1], s=50);
模型的bandwidth参数(bandwidth为高维球区域的半径)
from sklearn.cluster import estimate_bandwidth
# 通过下列代码可自动检测bandwidth值
# 从data中随机选取100个样本,计算每一对样本的距离,然后选取这些距离的0.2分位数作为返回值,当n_samples很大时,这个函数的计算量是很大的。
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=100)
print("bandwidth:",bandwidth)
bandwidth: 3.4671488859543973
from sklearn.cluster import MeanShift
"""
MeanShift(bandwidth=3.0723913799161027, bin_seeding=True, cluster_all=True,
min_bin_freq=1, n_jobs=1, seeds=None)
Parameters:
bandwidth : RBF内核里面的边界宽度
seeds : 初始化内核的种子
bin_seeding : 是否将所有的样本点作为簇中心
min_bin_freq :只接受min_bin_freq的点作为种子,以加速算法
cluster_all : 是否将所有数据点都分配到簇中,false表示将独立点进行独立(-1)
n_jobs : 并行计算数
Attributes:
cluster_centers_ : 簇中心点坐标
labels_ : 每个点的标签
"""
# bin_seeding设置为True就不会把所有的点初始化为核心位置,从而加速算法
ms = MeanShift(bandwidth=bandwidth, bin_seeding=True)
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
# 计算类别个数
labels_unique = np.unique(labels)
n_clusters = len(labels_unique)
print("number of estimated clusters : %d" % n_clusters)
number of estimated clusters : 3
import matplotlib.pyplot as plt
from itertools import cycle
from scipy.spatial.distance import cdist
pylab.rcParams['figure.figsize'] = (15.0, 8.0)
plt.scatter(X[:, 0], X[:, 1], c=labels, s=50, cmap='viridis')
#画出聚类中心
centers = cluster_centers
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.5);
plt.title("Mean Shift (clusters = %d , Bandwidth = %.1f)"%(n_clusters,bandwidth),fontsize=20);
plt.show()
4.2 DBSCAN算法
基本思想:如果一个点p和另一个点q是密度相
连的,则p和q属于同一个簇。
4.2.1 相关的概念
-
邻域:p点的r邻域
N r ( p ) = q ∣ q 属 于 D 且 d i s t ( p , q ) < = r N_{r}(p)={ q | q属于D 且 dist(p,q)<=r } Nr(p)=q∣q属于D且dist(p,q)<=r -
核心点: 邻域中至少包含minpts个点(含中心点自身)
-
出发密度可达
-
密度相连关系
-
基于密度的簇: 连通性,极大性
4.2.2 dbscan算法思想
- 首先选取一个未标记类别的核心点,并创建一个新簇;
- 然后,寻找所有从该核心点出发关于ε和MinPts
- 密度可达的点,并标记为该簇。
- 重复这个过程,直至处理完所有点,即没有未标记簇的核心点
输入: 数据集D,邻域半径ε,最小点数MinPts
输出: 关于(ε, MinPts)的所有簇的集合
方法: 其过程描述如下:
do
{ 从数据集D中抽取一个未处理过的点p;
if (p是核心点)
找出所有从p出发关于(ε, MinPts)密度可达的点,形成一
个簇;
else
p是边界点或噪声点(非核心点),跳出本次循环,寻找下一
点;
} until (所有点都被处理);
- 优点是基于密度定义,相对抗噪音,能处理任意形状和大小的簇。
- 缺点 是对参数(ε, MinPts)敏感,当簇的密度变化太大时,会产生较大误差。
4.2.3 dbscan的算法思想2
- DBSCAN是一种基于密度的聚类算法,这类密度聚类算法一般假定类别可以通过样本分布的紧密程度决定。同一类别的样本,他们之间是紧密相连的,也就是说,在该类别任意样本周围不远处一定有同类别的样本存在。
- 通过将紧密相连的样本划为一类,这样就得到了一个聚类类别。通过将所有各组紧密相连的样本划为各个不同的类别,则我们就得到了最终的所有聚类类别结果.
- DBSCAN的两个重要参数:
- 参数(ϵ, MinPts)用来描述邻域的样本分布紧密程度。
- ϵ 描述了某一样本的邻域距离阈值,MinPts描述了某一样本的距离为ϵ的邻域中样本个数的阈值。
4.2.4 代码实现1
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import pylab
pylab.rcParams['figure.figsize'] = (15.0, 8.0)
# X 创建300个随机坐标,范围是[-6,6]
X=(np.random.rand(300,2)*12)-6
# Y 创建300个随机坐标,范围是[0,1]
y=np.random.randint(0,2,size=(300,1))
#plt.scatter(X[:, 0], X[:, 1], s=50);
"""
DBSCAN(eps=0.5, min_samples=5, metric='euclidean', metric_params=None,
algorithm='auto', leaf_size=30, p=None, n_jobs=1)
Parameters:
eps : 两个样本之间的最大距离
min_samples : 点的邻域中的样本数
metric : 特征数组中计算两个实例之间的距离的矩阵
metric_params:最近邻距离度量参数。
algorithm : 计算最近邻点的算法
leaf_size : BallTree 或 cKDTree 的叶子数量
p : 最近邻距离度量参数
n_jobs : 并行任务数
Attributes:
core_sample_indices_ : 核心样本的索引
components_ : 通过训练获得核心样本的副本
labels_ : 聚类标签
"""
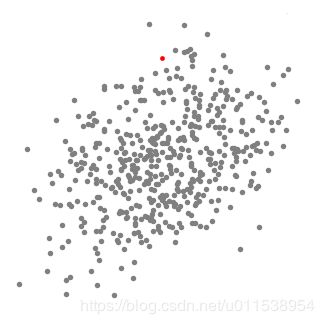
dbsc = DBSCAN(eps = .5, min_samples = 6).fit(X)
y_true = dbsc.labels_
plt.scatter(X[:,0],X[:,1],c=y_true)
plt.show()
4.2.4 代码实现2
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import pylab
pylab.rcParams['figure.figsize'] = (8.0, 4.0)
from sklearn.datasets import make_moons
# moons_X:数据 moon_y: 标签
moons_X, moon_y = make_moons(n_samples = 2000)
print(moons_X.shape)
print(moon_y.shape)
(2000, 2)
(2000,)
plt.scatter(moons_X[:,0],moons_X[:,1],c=moon_y,cmap='viridis')
def add_noise(X,y, noise_level = 0.01):
#噪声数据点个数
amt_noise = int(noise_level*len(y))
#随机产生
idx = np.random.choice(len(X), size = amt_noise)
#将噪声点加入数据集
noise = np.random.random((amt_noise, 2) ) -0.5
X[idx,:] += noise
return X
add_noise(moons_X,moon_y)
plt.scatter(moons_X[:,0],moons_X[:,1],c=moon_y,cmap='viridis')
plt.title(" Half-moons data by adding noise",fontsize=20);
 process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3UwMTE1Mzg5NTQ=,size_16,color_FFFFFF,t_70)
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3UwMTE1Mzg5NTQ=,size_16,color_FFFFFF,t_70)
dbsc = DBSCAN(eps = .05, min_samples = 3).fit(moons_X)
y_true = dbsc.labels_
plt.scatter(moons_X[:,0],moons_X[:,1],c=y_true)
plt.show()
4.3 OPTICS算法
- 点的核心距离:
- 输入:点,包含点数量
- 条件: 点为核心点
- 输出距离阈值(最小值)
- 表示点的特征不一样,地位不一样
- 可达距离:
- p关于o的可达距离: o的核心距离, po的距离, 取最大值
- o是核心点
- 簇排序:
- 可达距离排序
- 核心点的可达距离是核心距离
- 邻域范围内的点的可达距离是核心距离
- 邻域外的点可达距离, 是op的距离
- 每个点的属性:
- 他的核心点
- 他到核心点的可达距离
- 可达距离排序