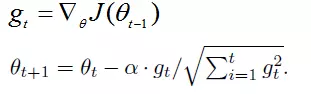深度学习最全优化方法总结比较（SGD，SGDM,Adam,Adagrad，Adadelta，Adam）

     拿来药材（数据），架起八卦炉（模型），点着六味真火（优化算法），就摇着蒲扇等着丹药出炉了。

不过，当过厨子的都知道，同样的食材，同样的菜谱，但火候不一样了，这出来的口味可是千差万别。火小了夹生，火大了易糊，火不匀则半生半糊。

      机器学习也是一样，模型优化算法的选择直接关系到最终模型的性能。有时候效果不好，未必是特征的问题或者模型设计的问题，很可能就是优化算法的问题。

     说到优化算法，入门级必从SGD学起，老司机则会告诉你更好的还有AdaGrad/AdaDelta，或者直接无脑用Adam。可是看看学术界的最新paper，却发现一众大神还在用着入门级的SGD，最多加个Moment或者Nesterov ，还经常会黑一下Adam。

---

病态矩阵是一种特殊矩阵。指条件数很大的非奇异矩阵。病态矩阵的逆和以其为系数矩阵的方程组的界对微小扰动十分敏感，对数值求解会带来很大困难。 

在求解任何反问题的过程中通常会遇到病态矩阵问题，而且病态矩阵问题还未有很好的解决方法，尤其是长方形、大型矩阵。目前主要有Tikhonov、奇异值截断、奇异值修正、迭代法等方法。

求解方程组时对数据的小扰动很敏感的矩阵。

解线性方程组Ax=b时，若对于系数矩阵A及右端项b的小扰动 δA、δb，方程组 (A+δA)χ=b+δb的解 χ 与原方程组Ax=b的解差别很大，则称矩阵A为病态矩阵。方程组的近似解 χ 一般都不可能恰好使剩余 r=b-Aχ 为零，这时 χ 亦可看作小扰动问题Aχ=b-r(即δA=0，δb=-r) 的解，所以当A为病态时，即使剩余很小，仍可能得到一个与真解相差很大的近似解。

判定矩阵是否病态以及衡量矩阵的病态程度通常是看矩阵A的条件数K(A)=‖A-1‖*‖A‖ 的大小，其中 A-1 为矩阵 A 的逆， ‖‖ 表示对矩阵取某一种范数。 K(A) 称为 A 的条件数，它很大时，称 A 为病态，否则称良态； K(A) 愈大， A 的病态程度就愈严重。

---

动量梯度的概念

动量梯度下降法的核心便是对一系列梯度进行指数加权平均

使用指数加权平均之后梯度代替原梯度进行参数更新。因为每个指数加权平均后的梯度含有之前梯度的信息，动量梯度下降法因此得名。

1 mini-batch梯度下降法
在实际应用中，由于样本数量庞大，训练数据上百万是很常见的事。如果每执行一次梯度下降就遍历整个训练样本将会耗费大量的计算机资源。在所有样本中随机抽取一部分(mini-batch)样本，抽取的样本的分布规律与原样本基本相同，事实发现，实际训练中使用mini-batch梯度下降法可以大大加快训练速度。

1.1 实现方法
mini-batch梯度下降法的思想很简单，将样本总体分成多个mini-batch。例如100万的数据，分成10000份,每份包含100个数据的mini-batch-1到mini-batch-10000，每次梯度下降使用其中一个mini-batch进行训练，除此之外和梯度下降法没有任何区别。

1.2 直观体验

由于mini-batch每次仅使用数据集中的一部分进行梯度下降，所以每次下降并不是严格按照朝最小方向下降，但是总体下降趋势是朝着最小方向，上图可以明显看出两者之间的区别。

对右边的图来说，动量梯度下降法并没有什么用处。梯度批量下降法主要是针对mini-batch梯度下降法进行优化，优化之后左右的摆动减小，从而提高效率。优化前后的对比如下图，可见动量梯度下降法的摆动明显减弱。

2 指数加权平均
指数加权平均值又称指数加权移动平均值，局部平均值，移动平均值。加权平均这个概念都很熟悉，即根据各个元素所占权重计算平均值。指数加权平均中的指数表示各个元素所占权重呈指数分布。

---

优化算法框架

优化算法框架

神经网络模型中有多种优化算法，优化算法的作用用来优化更新参数。
对于优化算法而言，主要的框架如下。
参数：转存失败重新上传取消转存失败重新上传取消 目标函数：转存失败重新上传取消转存失败重新上传取消 学习率转存失败重新上传取消转存失败重新上传取消。
对于每个epoch t：
step1：计算当前梯度转存失败重新上传取消转存失败重新上传取消
step2：计算动量。
     一阶动量：转存失败重新上传取消转存失败重新上传取消
     二阶动量:转存失败重新上传取消转存失败重新上传取消
step3：计算当前时刻下降梯度 转存失败重新上传取消转存失败重新上传取消
step4：更新参数 转存失败重新上传取消转存失败重新上传取消
对于不同的优化算法而言，区别主要在于第一步和第二步。对于梯度的计算，一阶动量的计算，和二阶动量的计算存在差别。
三、四步的计算更新，各个算法之间都是相同的。

SGD

基本的mini-batch SGD优化算法在深度学习取得很多不错的成绩。然而也存在一些问题需解决：

1. 选择恰当的初始学习率很困难。

2. 学习率调整策略受限于预先指定的调整规则。

3. 相同的学习率被应用于各个参数。

4. 高度非凸的误差函数的优化过程，如何避免陷入大量的局部次优解或鞍点。

SGDM

也就是SGD+ Momentum。这里引入了一阶动量。
从直观理解就是加入了一个惯性，在坡度比较陡的地方，会有较大的惯性，这是下降的多。坡度平缓的地方，惯性较小，下降的会比较慢。
修改SGD中的一阶动量为
转存失败重新上传取消转存失败重新上传取消
等式右边有两部分，加号左边的部分为之前积累的下降方向，加号右边为当前的梯度。两者的权重用参数来控制。
转存失败重新上传取消转存失败重新上传取消越大，说明下降的方向越依赖于以往的惯性。可以减少方向的突变。

后续的更新保留了之前的梯度，但最近的梯度权重更高

AdaGrad(Adaptive Gradient),自适应步长,历史梯度平方和的平方根

AdaGrad）为每一个参数保留一个学习率以提升在稀疏梯度（即自然语言和计算机视觉问题）上的性能

公式：

gt表示第t时间步的梯度（向量，包含各个参数对应的偏导数，gt,i表示第i个参数t时刻偏导数）

gt2表示第t时间步的梯度平方（向量，由gt各元素自己进行平方运算所得，即Element-wise）

与SGD的核心区别在于计算更新步长时，增加了分母：梯度平方累积和的平方根。此项能够累积各个参数gt,i的历史梯度平方，频繁更新的梯度，则累积的分母项逐渐偏大，那么更新的步长(stepsize)相对就会变小，而稀疏的梯度，则导致累积的分母项中对应值比较小，那么更新的步长则相对比较大。

AdaGrad能够自动为不同参数适应不同的学习率（平方根的分母项相当于对学习率α进进行了自动调整，然后再乘以本次梯度），大多数的框架实现采用默认学习率α=0.01即可完成比较好的收敛。

优势：在数据分布稀疏的场景，能更好利用稀疏梯度的信息，比标准的SGD算法更有效地收敛。

缺点：主要缺陷来自分母项的对梯度平方不断累积，随之时间步地增加，分母项越来越大，最终导致学习率收缩到太小无法进行有效更新。

RMSPropt（梯度平方根）

RMSprop，全称root mean square prop。也用到权重超参数beta（一般取0.999），和Momentum相似：

 

其中dW的平方是(dW)^2，db的平方是(db)^2。如果严谨些，防止分母为0，在分数下加上个特别小的一个值epsilon，通常取10^-8。

Adam

Adam 是一种在深度学习模型中用来替代随机梯度下降的优化算法。

Adam 结合了 AdaGrad 和 RMSProp 算法最优的性能，它还是能提供解决稀疏梯度和噪声问题的优化方法。

Adam 的调参相对简单，默认参数就可以处理绝大部分的问题。

---

总结:

参考文献

动量梯度下降法(gradient descent with momentum)

https://blog.csdn.net/weixin_36811328/article/details/83451096

详解深度学习中的常用优化算法(写的非常好)

https://mp.weixin.qq.com/s/Bu9GDxQQRaw74uLFPteI5w

深度学习在美团推荐平台排序中的运用

https://tech.meituan.com/2017/07/28/dl.html