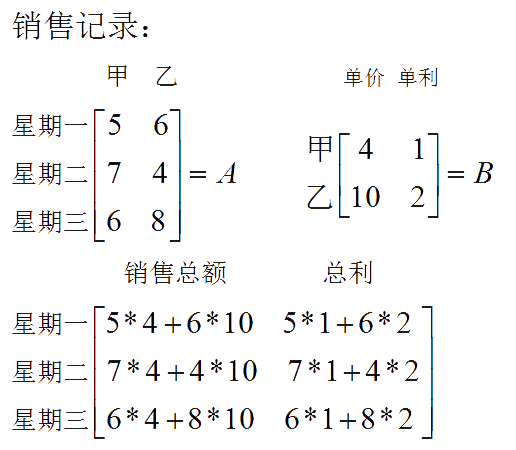线性代数 矩阵及其运算
一.数学概念
在数学中,矩阵(Matrix)是指纵横排列的二维数据表格
定义1.1 由 个数 排成m行n列的数表
称为m行n列的矩阵,简称 矩阵,记作
1.单位矩阵
在矩阵的乘法中,有一种矩阵起着特殊的作用,如同数的乘法中的1,我们称这种矩阵为单位矩阵.它是个方阵,从左上角到右下角的对角线(称为主对角线)上的元素均为1以外全都为0。对于单位矩阵,有AE=EA=A
二.原理,公式和法则
1.矩阵的加法在数学里,矩阵加法一般是指两个矩阵把其相对应元素加在一起的运算。
1.矩阵的加法
(1) 公式
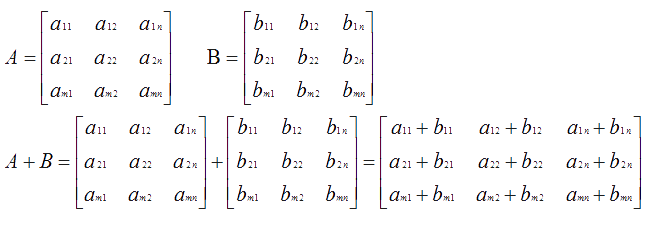
(2) 运算律
A + B = B + A
A + B + C = A + ( B + C )
A + (-A) = 0
A + 0 = 0
2.数乘矩阵
一个矩阵乘上一个数等于矩阵的每个元素乘上这个数
(1) 公式

(2) 运算律
λA = Aλ
(λμ)A = λ(μA)
(λ+μ)A = λA+μA
λ(A+B) = λA+λB
3.矩阵与矩阵相乘
(1) 设A = (aij)是一个m*s矩阵,B = (bij)是一个s*n的矩阵那么规定矩阵A与矩阵B的乘积是一个m*n的矩阵C = (cij)
并把此乘积记作C=AB
将矩阵A对应i行上的每一个元素*矩阵B上的对应i列上的每一个元素相加就得到矩阵C的Cij元素的值
两矩阵相乘的前提条件:“第一个矩阵的行数 = 第二个矩阵的列数”
通过下面一个销售统计的一个计算过程,有助于我们理解矩阵相乘的概念:
(2) 运算律(假设运算都是可行的):
1)结合律:ABC = A(BC)
2) 数与矩阵乘法的结合律:λ(AB) = (λA)B = A(λB) (其中λ是常数)
3)左分配律:A(B+C) = AB+BC
右分配律: (A+B)C = AC+BC
4) 对于单位矩阵Em,容易验证:
EmAm*n = Am*n, Am*n*Em = Am*n
也就是:AE = EA = A
(3) 注意:
矩阵的乘法与通常数的乘法有很大区别,特别应该注意的是:
1)矩阵乘法不满足交换律,一般来讲即便AB有意义,BA也未必有意义;
2) 两个非零矩阵的乘积可能是零矩阵,即AB=0未必能推出A=0或者B=0;
3)如果AB=AC并且A≠0未必有B=C;