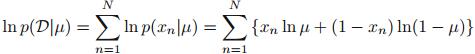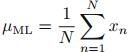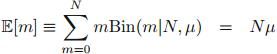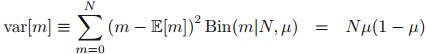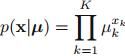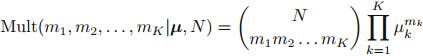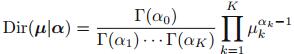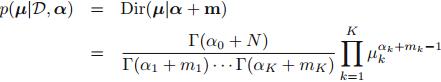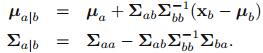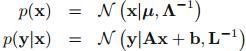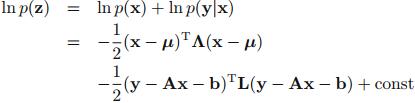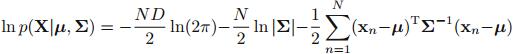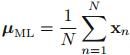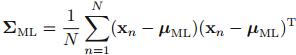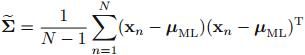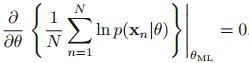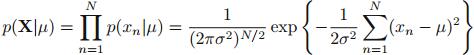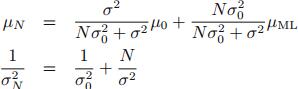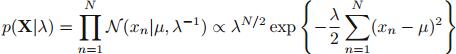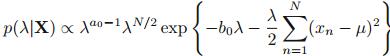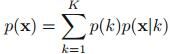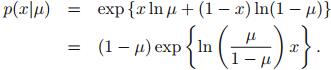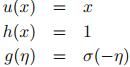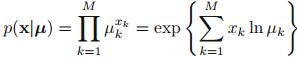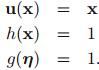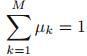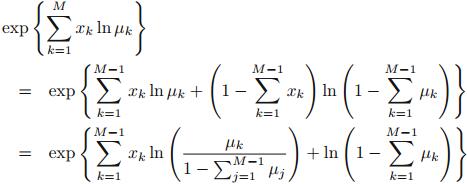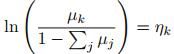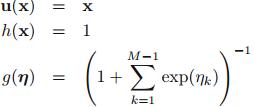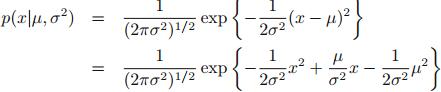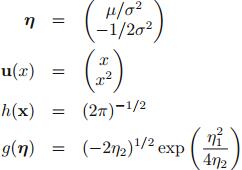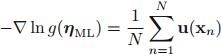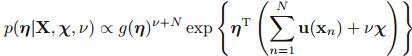模式识别与机器学习(二):常用的概率分布(共轭分布等)
第二章主要介绍几个重要的概率分布及其特性。
1. 二值变量的概率分布
假设一个二元随机变量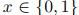 ,用参数
,用参数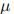 表示
表示 的概率为:
的概率为: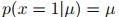 。
。
(1)伯努利分布(Bernoulli distribution)
概率分布函数:
期望:
方差:
log似然函数为:
其中,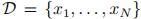 表示变量x的观测值。得到
表示变量x的观测值。得到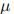 的最大似然估计值为:
的最大似然估计值为:
(2)二项分布(Binomial distribution)
概率分布函数:
期望:
方差:
注:对于小的数据集,如果对二项分布采用极大似然估计,会得到过拟合(over-fitting)的估计结果。可以采用贝叶斯方法,引入共轭先验分布(conjugate prior distribution)来解决这个问题。共轭先验是指,选取一个与似然函数共轭的先验分布,使得后验分布与先验分布有同样的函数形式。其中,二项分布的共轭先验是Beta分布。
(3)Beta分布
概率分布函数:
期望:
方差:
采用贝叶斯方法,将Beta先验乘以二项分布似然函数,得到后验分布如下:
2. 多项式变量的概率分布
(1)多项式分布(Multinomial distribution)
概率函数为:
(2)狄利克雷分布(Dirichlet distribution)
狄利克雷分布是多项式分布的共轭先验分布。概率分布函数如下:
采用贝叶斯方法,得到后验分布如下:
3. 高斯分布
一元概率分布函数:
多元概率分布函数:
3.1 条件高斯分布(Conditional Gaussian distribution)
假设x是一个服从高斯分布的D维向量,为了讨论条件高斯分布,将x分成两个独立的子集:
这两个子集对应的期望为:
对应的方差为:
经推导,条件概率分布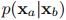 的期望和方差分别为:
的期望和方差分别为:
3.2 边缘概率分布(Marginal Gaussian distribution)
以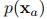 为例,其期望和方差分别为:
为例,其期望和方差分别为:
3.3 高斯变量的贝叶斯理论
本节的主要内容是:已知高斯边缘概率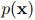 和高斯条件概率
和高斯条件概率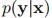 (其均值是变量x的线性函数,且其方差与x无关),如何求得边缘概率
(其均值是变量x的线性函数,且其方差与x无关),如何求得边缘概率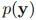 和条件概率
和条件概率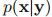 。
。
求解方法是,首先求解联合概率分布的函数形式,再利用3.1节和3.2节中边缘概率分布和条件概率分布的期望和方差公式求得结果。
假设已知:
经推导得,期望和方差分别为:
根据3.2节,得到边缘概率分布的期望和方差分别为:
根据3.1节,得到条件概率分布的期望和方差为:
3.4高斯最大似然估计
给定数据集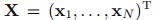 ,假定这些观测值都是独立地从高斯分布中产生。为了估计高斯分布函数中的参数,可以采用最大似然估计。其中,log似然函数为:
,假定这些观测值都是独立地从高斯分布中产生。为了估计高斯分布函数中的参数,可以采用最大似然估计。其中,log似然函数为:
得到的期望和方差的估计值为:
其中,方差的无偏估计为:
3.5 顺序估计(Sequential estimation)
顺序估计适用于在线应用,可以一次只处理一个数据,根据当前数据估计参数值。假设需要被顺序估计的参数为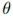 ,采用极大似然估计得到:
,采用极大似然估计得到:
为了进行顺序估计,可以采用Robbins-Monro算法:
该算法的特点在于估计值会收敛到根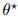 ,根满足
,根满足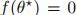 。
。
3.6 高斯分布的贝叶斯推理
本节的重点是,如果用贝叶斯理论估计高斯分布的均值或方差,需要选择哪些分布作为共轭先验。
3.6.1 单变量高斯分布
(1)方差已知,估计均值:
似然函数是:
共轭先验是:
后验分布是:
即:
其中:
(2)均值已知,估计方差:
似然函数是:
共轭先验是Gamma分布:
后验分布是:
(3)均值和期望未知:
共轭分布为高斯伽马分布(Gaussian-gamma distribution):
3.6.2 多变量高斯分布
(1)方差已知,估计均值,采用的共轭先验还是高斯分布;
(2)均值已知,方差未知,采用Wishart分布:
(3)均值和方差都未知,采用Gaussian-Wishart分布:
3.7 学生t分布(Student's t-distribution)
Student's t-distribution可以通过叠加无限个均值相同而方差不同的高斯分布获得。与高斯分布相比,t分布对离群点更不敏感,因此鲁棒性(robustness)更高。
3.8 周期变量(Periodic variables)
高斯分布不适合作为一些连续变量(例如:周期变量)的密度分布函数。对于周期变量,可以采用对高斯分布进行周期泛化后的von Mises分布:
von Mises分布的局限性在于,该分布是单峰的,不能表示多峰分布。
3.9 高斯混合(Mixtures of Gaussians)
4. 指数分布族
本章节提到的很多分布函数(除了高斯混合分布)属于同一类分布——指数分布族,其分布函数形式如下:
(1)伯努利分布
推导出指数分布族形式:
得到:
所以:
该函数称为logistic/sigmoid函数。其他对应部分为:
(2)多项式分布
推导出指数分布族形式:
其中,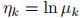 。其他对应部分为:
。其他对应部分为:
不过这里有一个限制条件:
在某些情况下,去除这个条件更方便时会用。方法是用前M-1项来表示第M项,则多项式分布推导为:
其中:
所以:
该函数称为softmax函数(也叫标准化指数)。其他对应部分为:
(3)单变量高斯分布
推导出指数分布族形式:
对应部分为:
4.1 最大似然与充分统计量
由于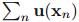 包含了最大似然估计器需要从数据中获取的全部信息,所以它被称为充分统计量。
包含了最大似然估计器需要从数据中获取的全部信息,所以它被称为充分统计量。
4.2 共轭先验
指数分布族选择的共轭先验符合以下形式:
对应的后验分布为:
4.3 无信息先验
当我们对未知的分布形式的先验知识不了解时,我们希望选择一种尽可能不影响后验分布的先验,称之为无信息先验。目的是为了让后验分布只取决于数据集本身。一般情况下,满足位置不变性或尺度不变性的分布可以作为无信息先验分布。
5 非参数方法
在本节之前讨论的都是参数估计方法。该方法采用具有特定函数形式和参数的概率分布,且这些参数值是由数据集决定的。参数方法的不足在于,如果选择的分布不符合数据本身所表示的概率分布,那么得到的预测结果会比较差。而非参数方法则不需要选择概率分布,避免了选错概率分布的问题。本节介绍三种非参数方法。
(1)条形图密度估计(Histogram density models)
主要方法是,指定条形图宽度(即把[0, 1]分割成多个区间),然后统计数据集中落入每个区间的数据量。特点是每个被统计完的数据都可以被丢弃,因而该方法可以顺序处理数据(例如在线数据)。但这个方法有两个问题,第一个是密度估计是不连续的,相邻的条形图之间有密度的断层;第二个是不适用于高维数据。不过接下来的两个方法可以解决该问题。
(2)核密度估计(Kernel density estimation)
主要方法是,指定一个单位空间大小(即指定核函数,例如高斯核函数),然后在数据集中按照该单位空间下包含的数据个数来决定相应的概率密度。
由于单位空间大小是固定的,该方法存在两个问题:第一,若单位空间过大,将导致某个高密度区域对应的密度曲线过于平滑,而不能反映真实的密度变化情况;第二,若单位空间过小,则会使密度曲线中存在很多噪音,曲线不平滑。
(3)近邻方法(Nearest-neighbour methods)
主要方法是,指定数据个数K,以某个数据为中心,查找距离该数据最近的数据点,当数据个数达到K时,则估计该区域的密度。
该方法可以解决核密度估计造成的第一个问题。同时,若K的值太小,会造成较大的噪音;若K的值太大,则密度曲线过于平滑,不能反映密度变化情况。所以需要选择一个大小适中的K值。