数据结构与算法基础(java版)学习路线+示图+代码
数据结构:结构决定功能,结构不同,功能不同。
算法:程序灵魂之所在(没有最好,只有最优)。
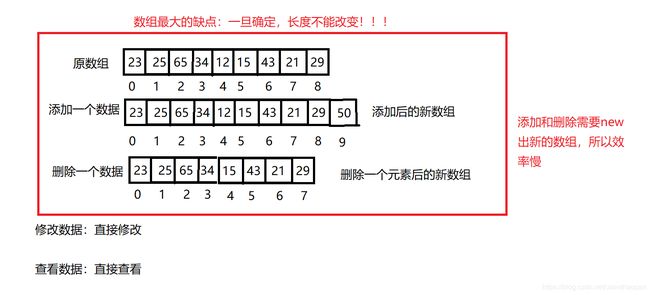
数组
数组中添加数据
public static void main(String[] args) {
//原来的数组
int[] arr=new int[] {23,43,12,56,76,89,43};
//查看数组中的数据
System.out.println(Arrays.toString(arr));
//需要增加的元素
int add=80;
//定义新的数组
int[] newArr=new int[arr.length+1];
//数组的赋值
for(int i=0;i<newArr.length-1;i++) {
//将原来数组中的数字据给新的数组
newArr[i]=arr[i];
}
//需要增加的数字加进去
newArr[newArr.length-1]=add;
//将新的数组给新的数组
arr=newArr;
System.out.println(Arrays.toString(arr));
}
数组中删除数据
public static void main(String[] args) {
//原来的数组
int[] arr=new int[] {15,63,45,23,78,15};
//查看数组
System.out.println(Arrays.toString(arr));
//需要删除的数字的下标
int index=0;
//定义新的数组
int[] newArr=new int[arr.length-1];
//数组的赋值
for(int i=0;i<newArr.length;i++) {
//删除的数字之前
if(i<index) {
newArr[i]=arr[i];
//删除数字之后的数字
}else {
newArr[i]=arr[i+1];
}
}
//将新的数组给原来的数组
arr=newArr;
System.out.println(Arrays.toString(arr));
}
数组中修改指定的数据
public static void main(String[] args) {
//原有的数组
int[] arr=new int[] {23,12,41,57,76,78,39};
//需要修改数组中数据的下标
int index=3;
//将数据修改为
int to=100;
//查看未修改前的数组
System.out.println("修改前:"+Arrays.toString(arr));
//修改
arr[index]=to;
//查看修改后的数组中的数据
System.out.println("修改后:"+Arrays.toString(arr));
}
在数组中指定位置插入数据
/**
* 在数组中指定位置的插入数据
* @param arr 原来的数组
* @param index 插入位置的下标
* @param data 插入的数据
* @return 删除后的数组
*/
private static int[] insertConfirm(int[] arr,int index, int data) {
//定义新的数组
int[] newArr=new int[arr.length+1];
//遍历数组
for(int i=0;i<arr.length;i++) {
//判断当前遍历的下标与目标位置的大小
if(i<index) {
//将目标位置之前的数据放入到新数组中
newArr[i]=arr[i];
}else {
//将目标位置后的数据放到新的数组中去
newArr[i+1]=arr[i];
}
}
//将需要插入的数据放进新的数组
newArr[index]=data;
return newArr;
}
删除数组中指定位置的数据
/**
* 删除数组中指定位置的数据
* @param arr 原来的数组
* @param index 删除数据的下标
* @return 删除后的数组
*/
private static int[] deleteConfirm(int[] arr, int index) {
// 定义新的数组
int[] newArr=new int[arr.length-1];
//遍历数组
for(int i=0;i<newArr.length;i++) {
//比较操作的位置与当前遍历位置的大小
if(i<index) {
//将此位置之前的数据给新数组
newArr[i]=arr[i];
}else {
//将之后的数字给新数组
newArr[i]=arr[i+1];
}
}
return newArr;
}
数据查找之线性查找
/**
* 线性查找
* @param arr 查找的数组
* @param findData 需要查找的数组
* @return 查找数字所在的位置
*/
private static int lineSearch(int[] arr,int findData) {
// 查找数字的下标(没有则返回-1)
int index=-1;
//遍历数组
for(int i=0;i<arr.length;i++) {
//判断是否要找的数字
if(arr[i]==findData) {
//将下标给index
index=i;
//跳出循环
break;
}
}
return index;
}
数据查找之二分查找
二分查找法适用条件:数据序列有序
/**
* 二分查找法
* @param arr 查找的数组
* @param target 查找的目标数
* @return 目标数所在的位置
*/
private static int binarySearch(int[] arr, int target) {
// 查找数据的下标(不存在返回-1)
int index=-1;
//开始的位置
int start=0;
//结束的位置
int end=arr.length-1;
//中间的位置
int mid=(start+end)/2;
//循环遍历
while(true) {
//如果中间位置的数字刚好等于目标数
if(arr[mid]==target) {
index=mid;
break;
}else {
//如果中间数字小于目标数字
if(arr[mid]<target) {
//向后移动开始的下标
start=end+1;
//将
}else {
//向前移动结束的下标
end=end-1;
}
}
//改变中间的位置
mid=(start+end)/2;
}
return index;
}
栈(数组模拟栈)
特点:先进后出(摞盘子)
MyStack.java
package test2;
/**
* 用数组模拟栈
* @author Mr.Zhao
* @version jdk 1.8 tomcat 8.5
* @2020年5月5日
* @下午4:29:23
*/
public class MyStack {
int[] arr;
public MyStack() {
arr=new int[0];
}
//压栈
public int[] push(int a) {
int[] newArr=new int[arr.length+1];
for(int i=0;i<arr.length;i++) {
newArr[i]=arr[i];
}
newArr[arr.length]=a;
arr=newArr;
return arr;
}
//弹栈
public int pop() {
//取出数组中最后一个元素
int num=arr[arr.length-1];
//创建一个新的数组
int[] newArr=new int[arr.length-1];
//将为去除的数组数据放到新的数组中
for(int i=0;i<newArr.length;i++) {
newArr[i]=arr[i];
}
//原来数组代替新的数组
arr=newArr;
return num;
}
//查看栈顶元素
public int peek() {
return arr[arr.length-1];
}
//判断栈是否为空
public boolean isNull() {
if(arr.length==0) {
return true;
}
return false;
}
}
栈的测试:
TestMyStack.java
package test2;
public class TestMyStack {
public static void main(String[] args) {
MyStack my=new MyStack();
my.push(1);
my.push(2);
my.push(3);
my.push(4);
my.push(5);
my.push(6);
System.out.println(my.pop());
System.out.println(my.pop());
System.out.println(my.pop());
System.out.println(my.pop());
System.out.println(my.pop());
System.out.println(my.pop());
System.out.println(my.isNull());
}
}
队列(数组模拟队列)
特点:先进先出(医院看病)
MyQueue.java
package test4;
/**
* 数组模拟队列
* @author Mr.Zhao
* @version jdk 1.8 tomcat 8.5
* @2020年5月5日
* @下午6:15:57
*/
public class MyQueue {
int[] nums;
public MyQueue() {
nums=new int[0];
}
//入队
public void add(int a) {
//创建新的数组
int[] newArr=new int[nums.length+1];
//数组赋值
for(int i=0;i<nums.length;i++) {
newArr[i]=nums[i];
}
//将新添加的元素加到新的数组中去
newArr[nums.length]=a;
//将新的数组给原来的数组
nums=newArr;
}
//出队
public int pool() {
int date=nums[0];
//创建新的数组
int[] newArr=new int[nums.length-1];
//数组赋值
for(int i=0;i<nums.length-1;i++) {
newArr[i]=nums[i+1];
}
//将新的数组给原来的数组
nums=newArr;
return date;
}
//判断队列是否为空
public boolean isNull() {
return nums.length==0;
}
}
队列测试:
Test.java
package test4;
public class Test {
public static void main(String[] args) {
MyQueue my=new MyQueue();
my.add(1);
my.add(2);
my.add(3);
my.add(4);
my.add(5);
System.out.println(my.pool());
System.out.println(my.pool());
System.out.println(my.pool());
System.out.println(my.pool());
System.out.println(my.pool());
System.out.println(my.isNull());
}
}
排序算法整合(冒泡排序,快速排序,插入排序,希尔排序,选择排序,归并排序,基数排序)
/**
* 归并排序
* @param arr 需要排序的数组
* @param start 开始的位置
* @param end 结束的位置
*/
public static void merge(int[] arr, int start, int end) {
if (start < end) {
// 中间位置
int middle = (start + end) / 2;
// 处理左边的数组
merge(arr, start, middle);
// 处理右边的数据
merge(arr, middle + 1, end);
// 归并
mergeSort(arr, start, middle, end);
}
}
/**
* 归并排序
* @param arr 需要排序的数组
* @param start 开始的位置
* @param middle 递增到递减的中间位置
* @param end 结束的位置
*/
private static void mergeSort(int[] arr, int start, int middle, int end) {
// 创建临时数字
int[] temp = new int[end - start + 1];
// 记录第一个数组需要遍历的下标
int i = start;
// 记录第二个数组的下标
int j = middle + 1;
// 临时数组的下标
int index = 0;
// 遍历两个数组比较两个数字,放到临时变量
while (i <= middle && j <= end) {
// 第一个数组中的数据更小
if (arr[i] <= arr[j]) {
// 将小的数据放到临时数组中区
temp[index] = arr[i];
// 将这个数组的下标往前移动
i++;
// 临时数组的下标加加
index++;
} else {
// 第二个数组中的数据更小
// 将这个数字据刚到临时数组中去
temp[index] = arr[j];
// 后面面数组的下标移动
j++;
// 临时数组的下标加加
index++;
}
}
// 处理后一个数组多余的数据
while (j <= end) {
temp[index] = arr[j];
j++;
index++;
}
// 处理前一个数组多余的数据
while (i <= middle) {
temp[index] = arr[i];
i++;
index++;
}
// 数组赋值
for (int k = 0; k < temp.length; k++) {
arr[k + start] = temp[k];
}
}
/**
* 选择排序:将第一个数字看成是最小的,将之后的数字依次与该数字进行比较,如果小于该数字,修改下标,并且交换位置,如果大于该数字,最小的数字下标位置不变
* 所以:第一轮结束后,序列中的最小的数字必定在最前面
* @param arr 需要排序的序列
* @return 排好后将该序列返回
*/
private static int[] selectSort(int[] arr) {
// TODO Auto-generated method stub
//遍历所有的数字
for(int i=0;i<arr.length;i++) {
//将第一个数字看作是最小的,记录其下标
int minMindex=i;
//从第二个开始遍历,依次与第一个进行比较
for(int j=i+1;j<arr.length;j++) {
//如果前一个大于后一个
if(arr[minMindex]>arr[j]) {
//修改最小值的下标
minMindex=j;
}
}
//如果minMindex不等于i,说明着找到了比前一个更小的数字
if(minMindex!=i) {
int temp=arr[minMindex];
arr[minMindex]=arr[i];
arr[i]=temp;
}
}
return arr;
}
/**
* 希尔排序:插入排序的一种(插入排序包括直接插入排序)。是为解决直接插入排序中的某些特定情况而提高效率的。例如:1,2,3,4,5,6,7,8,9,0
* @param arr 需要排序的数组
* @return 排序后返回的数组
*/
private static int[] shellSort(int[] arr) {
// TODO Auto-generated method stub
// 遍历所有的步长
for (int step = arr.length / 2; step > 0; step /= 2) {
// 遍历第一个步长之后的所有的元素
for (int i = step; i < arr.length; i++) {
// 遍历本组的数字
for (int j = i - step; j >= 0; j -= step) {
//当前的数字大于步长后的一个数字,交换位置
if (arr[j] >arr[j + step]) {
//定义临时变量,交换位置
int temp = arr[j];
arr[j] = arr[j + step];
arr[j + step] = temp;
}
}
}
}
return arr;
}
/**
* 二分查找:给出低座(序列的第一个)标和高座标(序列的最后一个)。
* 中间位置:(高座标+低座标)/2。如果需要找的目标数字刚好等于中间的数字,直接返回。否则,如果中间的位置刚好大于目标数,说明目标数在前半部分,
* 将结束的坐标向前移动。如果中间的位置的数字小于目标数,说明目标数字在后半部分,将开始的位置向后移动
*
* @param arr 找目标数字的数组
* @param target 需要找的目标数
* @return 目标数字所在位置的下标。如果数组中没有要找的数字,则返回-1
*/
private static int binarySearch(int[] arr, int target) {
// TODO Auto-generated method stub
// 开始的下标
int start = 0;
// 结束的下标
int end = arr.length - 1;
// 中间位置订单下标
int middle = (start + end) / 2;
// 目标数字所在的位置
int index = -1;
// 判断中间的数字是否需要找的数字
while (true) {
if (arr[middle] == target) {
index = middle;
break;
} else {
// 如果中间的数字大于目标数
if (arr[middle] > target) {
// 将开始的坐标从中间的位置向后移动
end = end - 1;
} else {
// 将结束的坐标向前移动
start = end + 1;
}
}
middle = (start + end) / 2;
}
return index;
}
/**
* 插入排序:将第一个数字看成是最小的,从后面依次比较。如过大于这个数,直接排在这个数的后面。如果小于这个数,将前一个数给后一个数。 会出现部分已经排好
* 的序列(独有 )
*
* @param arr
*/
private static void insertSort(int[] arr) {
// 从第一个数字开始向后遍历
for (int i = 1; i < arr.length; i++) {
// 如果这个数字大于后一个数字
if (arr[i - 1] > arr[i]) {
// 临时变量保存
int temp = arr[i];
// 排序概该数之前的数据
int j;
for (j = i - 1; j >= 0 && arr[j] >= temp; j--) {
// 将前一个数字给后一个数字
arr[j + 1] = arr[j];
}
// 此时出现数据小于临时变量
// 将临时变量给当前数据
arr[j + 1] = temp;
}
}
}
/**
* 快速排序:找个基准数(一般第一个),从后向前依次与基准数比较,如果比基准数大,位置不变,将下标向前移动。 如果比基准数小,则移动到基准数的左边。
* 当第一趟结束后,分别递归排序基准数的前面和后面的序列。
*
* @param arr 需要排序的数组
* @param start 需要排序的数组的开始位置
* @param end 需要排序的数组的结束位置
*/
private static void quickSort(int[] arr, int start, int end) {
// 递归的出口
if (start < end) {
// 基准数
int stand = arr[start];
// 高位
int high = end;
// 低位
int low = start;
// 找出比基准数大的数字和比基准数小的数字
while (low < high) {
// 找出比基准数大的数
while (low < high && arr[high] >= stand) {
// 高位的坐标向前移动
high--;
}
// 此时有一个数字比基准数小
// 将高位的数字给低位
arr[low] = arr[high];
// 找出比基准数小的数
while (low < high && arr[low] <= stand) {
// 低位的坐标向前移动
low++;
}
// 此时出现一个比基准数大的数
// 将低位的数字给高位
arr[high] = arr[low];
}
// 此时高位和低位重合
// 将基准数给重合的位置
arr[low] = stand;
// 递归排序基准数之前的数据
quickSort(arr, start, low);
// 递归排序基准数之后的数据
quickSort(arr, low + 1, end);
}
}
/**
* 冒泡排序:前两个数字先比较,如果前一个大于后一个,则交换位置
*
* @param arr 传入的数组
*/
private static void bubbleSort(int[] arr) {
// 遍历的趟数
for (int i = 0; i < arr.length; i++) {
// 每趟所要干的事情
for (int j = 0; j < arr.length - 1 - i; j++) {
// 如果前一个数字大于后一个数字
if (arr[j] > arr[j + 1]) {
// 定义临时变量保存数据
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
树
概述:数据的存储方式有线性存储和链式存储。
线性存储典型的是数组,链式存储典型的是链表。
但是对于数组来说:查找比较快,增加和删除比较慢。
对于链表来说:查找比较慢,增加和删除比较块。
那么,现在的需求是:我要查找,增加和删除都要快,又该如何解决?
所以有了树的结构。
二叉树
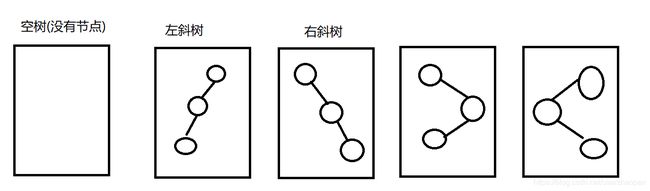
满二叉树
概述:所有叶子节点都在最后一层,而且节点总数为:2^n-1(n是树的高度)。
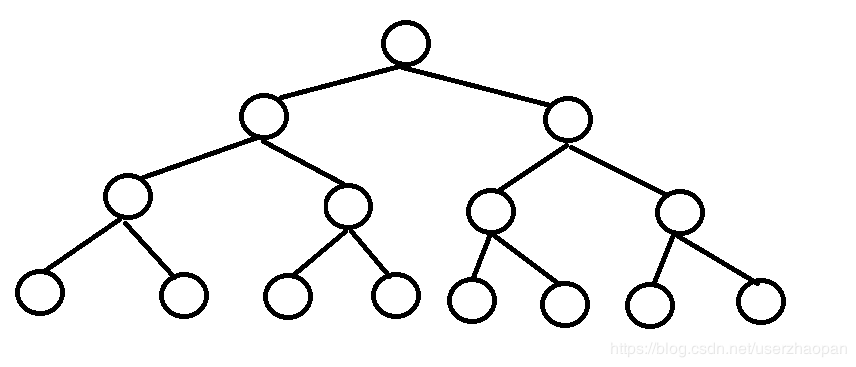
完全二叉树
概述:所有叶子节点都在最后一层或到数第二层 ,且最后一层的叶子节点在左边连续,到数第二层的叶子节点在右边连续。
树的5种形态
创建二叉树并遍历(前序,中序,后序),查找节点数据,并删除子树(链式)
树类:BinaryTree.java
package demo5;
public class BinaryTree {
Node root;
//设置根节点
public void setRoot(Node root) {
this.root = root;
}
//获取根节点
public Node getRoot() {
return root;
}
public void frontShow() {
if(root!=null) {
root.frontShow();
}
}
public void midShow() {
if(root!=null) {
root.midShow();
}
}
public void afterShow() {
if(root!=null) {
root.afterShow();
}
}
public Node frontSearch(int i) {
return root.frontSearch(i);
}
public void delete(int i) {
if(root.value==i) {
root=null;
}else {
root.delete(i);
}
}
}
节点类:Node.java
package demo5;
public class Node {
//节点的权
int value;
//左儿子
Node leftNode;
//右儿子
Node rightNode;
public Node(int value) {
this.value=value;
}
//设置左儿子
public void setLeftNode(Node leftNode) {
this.leftNode = leftNode;
}
//设置右儿子
public void setRightNode(Node rightNode) {
this.rightNode = rightNode;
}
//前序遍历
public void frontShow() {
//先遍历当前节点的内容
System.out.println(value);
//左节点
if(leftNode!=null) {
leftNode.frontShow();
}
//右节点
if(rightNode!=null) {
rightNode.frontShow();
}
}
//中序遍历
public void midShow() {
//左子节点
if(leftNode!=null) {
leftNode.midShow();
}
//当前节点
System.out.println(value);
//右子节点
if(rightNode!=null) {
rightNode.midShow();
}
}
//后序遍历
public void afterShow() {
//左子节点
if(leftNode!=null) {
leftNode.afterShow();
}
//右子节点
if(rightNode!=null) {
rightNode.afterShow();
}
//当前节点
System.out.println(value);
}
//前序查找
public Node frontSearch(int i) {
Node target=null;
//对比当前节点的值
if(this.value==i) {
return this;
//当前节点的值不是要查找的节点
}else {
//查找左儿子
if(leftNode!=null) {
//有可能可以查到,也可以查不到,查不到的话,target还是一个null
target = leftNode.frontSearch(i);
}
//如果不为空,说明在左儿子中已经找到
if(target!=null) {
return target;
}
//查找右儿子
if(rightNode!=null) {
target=rightNode.frontSearch(i);
}
}
return target;
}
//删除一个子树
public void delete(int i) {
Node parent = this;
//判断左儿子
if(parent.leftNode!=null&&parent.leftNode.value==i) {
parent.leftNode=null;
return;
}
//判断右儿子
if(parent.rightNode!=null&&parent.rightNode.value==i) {
parent.rightNode=null;
return;
}
//递归检查并删除左儿子
parent=leftNode;
if(parent!=null) {
parent.delete(i);
}
//递归检查并删除右儿子
parent=rightNode;
if(parent!=null) {
parent.delete(i);
}
}
}
测试类:TestBinaryTree.java
package demo5;
public class TestBinaryTree {
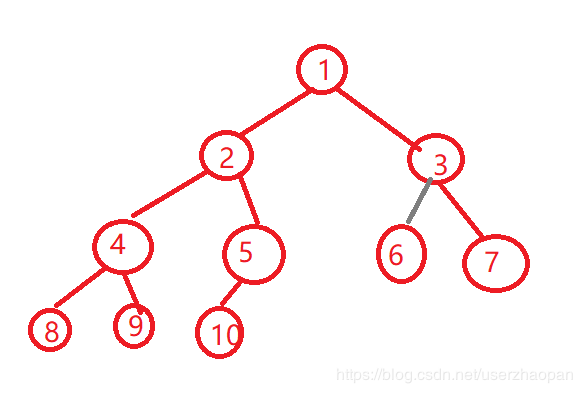
public static void main(String[] args) {
//创建一颗树
BinaryTree binTree = new BinaryTree();
//创建一个根节点
Node root = new Node(1);
//把根节点赋给树
binTree.setRoot(root);
//创建一个左节点
Node rootL = new Node(2);
//把新创建的节点设置为根节点的子节点
root.setLeftNode(rootL);
//创建一个右节点
Node rootR = new Node(3);
//把新创建的节点设置为根节点的子节点
root.setRightNode(rootR);
//为第二层的左节点创建两个子节点
rootL.setLeftNode(new Node(4));
rootL.setRightNode(new Node(5));
//为第二层的右节点创建两个子节点
rootR.setLeftNode(new Node(6));
rootR.setRightNode(new Node(7));
//前序遍历树
binTree.frontShow();
System.out.println("===============");
//中序遍历
binTree.midShow();
System.out.println("===============");
//后序遍历
binTree.afterShow();
System.out.println("===============");
//前序查找
Node result = binTree.frontSearch(5);
System.out.println(result);
System.out.println("===============");
//删除一个子树
binTree.delete(4);
binTree.frontShow();
}
}
散列表(哈希表)
概述:根据键快速定位到地址的值,获取该值。
线性查找:
-
数字序列无序
数字序列挨个比较,指导找到该数字。
最好情况:该目标数字在数字序列的第一个,只需比较一次。
最坏情况:该目标数字在数字序列的最后,需要比较序列的长度次。 -
数字序列有序
使用二分查找算法。
最好情况:目标数字在最中间,只需比较一次。
最坏情况:在序列两边(至少比无序的最坏情况好得多)
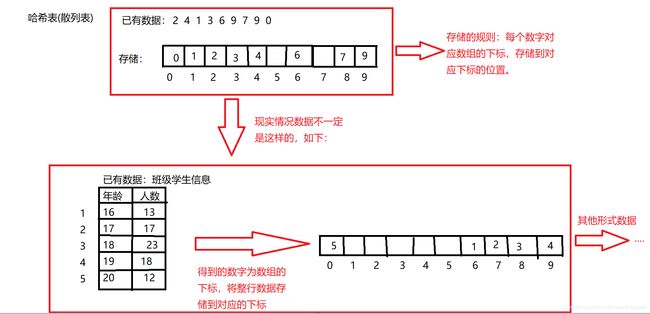
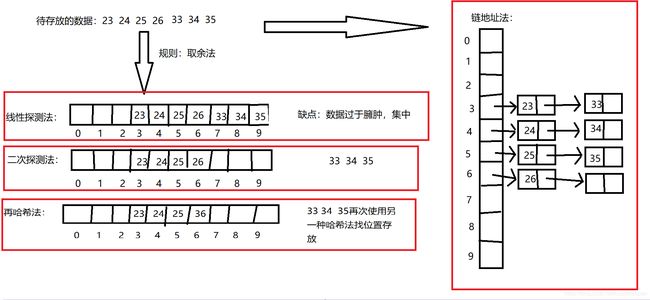
上述图中的规则就是:哈希函数(散列函数)
哈希函数的设计:
-
遵循的原则:计算简单,分布均匀
-
根据实际的数据进行设计
a.直接定址法(适用于小的数据):直接将数据放进去。
b.数字分析法(适用于较大数字,存放电话号码):事先知道数据,根据数据的特点分析。
c.平方取中法:13*13=169,将13放到6的下标位置。
d.取余法:23%10=3,将23放到3的下标位置。
e.随机数法:存储地址=random();
Student.java
package test6;
public class Student {
private int age;
private int count;
public int getAge() {
return age;
}
public void setAge(int age) {
this.age = age;
}
public int getCount() {
return count;
}
public void setCount(int count) {
this.count = count;
}
@Override
public String toString() {
return "Student [age=" + age + ", count=" + count + "]";
}
public Student(int age, int count) {
this.age = age;
this.count = count;
}
public Student(int age) {
this.age = age;
}
public Student() {
}
//哈希函数
public int hashCode() {
return this.age;
}
}
HashTable.java
package test6;
public class HashTable {
Student[] info=new Student[100];
//存放学生
public void add(Student student) {
int index=student.hashCode();
info[index]=student;
}
//取出学生
public Student out(Student student) {
int index=student.hashCode();
return info[index];
}
}
TestHashTable.java
package test6;
public class TestHashTable {
public static void main(String[] args) {
//创建几个学生对象
Student s1=new Student(12,2);
Student s2=new Student(13,15);
Student s3=new Student(14,13);
Student s4=new Student(15,18);
Student s5=new Student(16,8);
//创建哈希表对象
HashTable ht=new HashTable();
ht.add(s1);
ht.add(s2);
ht.add(s3);
ht.add(s4);
ht.add(s5);
//取出学生
Student out=new Student(16);
Student out2 = ht.out(out);
System.out.println(out2);
}
}
散列冲突(哈希冲突)
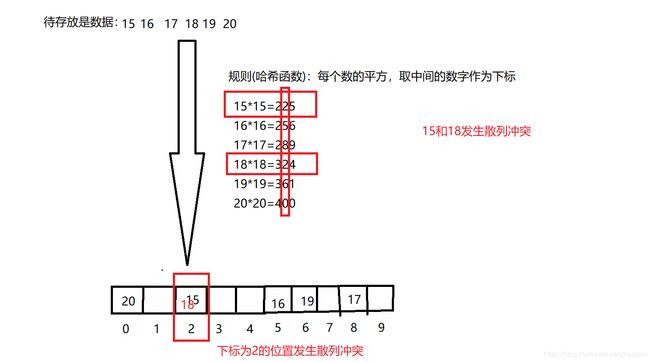
概述:位置已经有了一个数字,这时该位置又来一个数字。
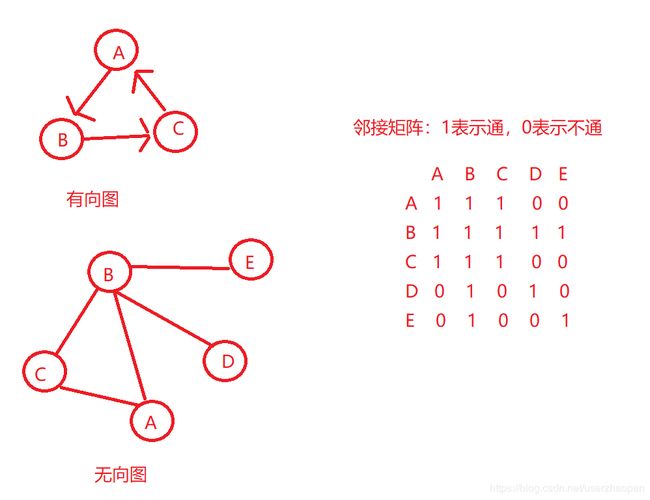
图
package test;
/**
* 顶点类
*/
public class Vertex {
private String value;
public boolean visited;
public String getValue() {
return value;
}
public void setValue(String value) {
this.value = value;
}
public Vertex(String value) {
super();
this.value = value;
}
@Override
public String toString() {
return value;
}
}
Graph.java
package test;
/**
* 图
*/
public class Graph {
//节点的数组
private Vertex[] vertex;
//节点数组的当前下标
private int currentSize;
//邻接矩阵
//0表示不通
//1表示连通
public int[][] adjMat;
private MyStack stack = new MyStack();
//当前遍历的下标
private int currentIndex;
public Graph(int size) {
vertex=new Vertex[size];
adjMat=new int[size][size];
}
/**
* 向图中加入一个顶点
* @param v
*/
public void addVertex(Vertex v) {
vertex[currentSize++]=v;
}
public void addEdge(String v1,String v2) {
//找出两个顶点的下标
int index1=0;
for(int i=0;i<vertex.length;i++) {
if(vertex[i].getValue().equals(v1)) {
index1=i;
break;
}
}
int index2=0;
for(int i=0;i<vertex.length;i++) {
if(vertex[i].getValue().equals(v2)) {
index2=i;
break;
}
}
adjMat[index1][index2]=1;
adjMat[index2][index1]=1;
}
}
package test;
import java.util.Arrays;
public class TestGraph {
public static void main(String[] args) {
Vertex v1 = new Vertex("A");
Vertex v2 = new Vertex("B");
Vertex v3 = new Vertex("C");
Vertex v4 = new Vertex("D");
Vertex v5 = new Vertex("E");
Graph g = new Graph(5);
g.addVertex(v1);
g.addVertex(v2);
g.addVertex(v3);
g.addVertex(v4);
g.addVertex(v5);
//增加边
g.addEdge("A", "C");
g.addEdge("B", "C");
g.addEdge("A", "B");
g.addEdge("B", "D");
g.addEdge("B", "E");
for(int[] a:g.adjMat) {
System.out.println(Arrays.toString(a));
}
}
}