智能算法之仿生算法

《MATLAB智能算法30个案例分析》
1、遗传算法（量子）
2、BP神经网络
3、粒子群算法
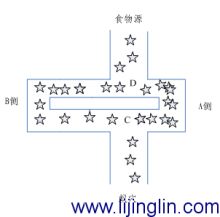
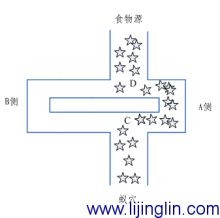
4、鱼群算法
5、模拟退火算法
6、蚁群算法

一、BP神经网络   

 原理（http://wenku.baidu.com/link?url=L737z2YWEJkSJk7QmW__NnKUw4nwuftKQb1Ks8CvbS6yKu9ZKgH2NMbWfXFkU0eVI69iAfErei4NKG4IkWx0UQ4sfew1nlRi6zRjficNPzy）

是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的

输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，

通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层（input）

、隐层(hide layer)和输出层(output layer)。

神经网络可以用作分类、聚类、预测等。我感觉，你的问题属于分类问题。
神经网络需要有一定量的历史数据，通过历史数据的训练，网络可以学习到数据中隐含的知识

虽然BP网络得到了广泛的应用，但自身也存在一些缺陷和不足，主要包括以下几个方面的问题：

首先，由于学习速率是固定的，因此网络的收敛速度慢，需要较长的训练时间。对于一些复杂问题，BP算法需要的训练时间可能非常长，这主要是由于学习速率太小造成的，可采用变化的学习速率或自适应的学习速率加以改进。

其次，BP算法可以使权值收敛到某个值，但并不保证其为误差平面的全局最小值，这是因为采用梯度下降法可能产生一个局部最小值。对于这个问题，可以采用附加动量法来解决。

再次，网络隐含层的层数和单元数的选择尚无理论上的指导，一般是根据经验或者通过反复实验确定。因此，网络往往存在很大的冗余性，在一定程度上也增加了网络学习的负担。

最后，网络的学习和记忆具有不稳定性。也就是说，如果增加了学习样本，训练好的网络就需要从头开始训练，对于以前的权值和阈值是没有记忆的。但是可以将预测、分类或聚类做的比较好的 权值保存。

1 传统的BP算法简述

　　BP算法是一种有监督式的学习算法，其主要思想是：输入学习样本，使用反向传播算法对网络的权值和偏差进行反复的调整训练，使输出的向量与期望向量尽可能地接近，当网络输出层的误差平方和小于指定的误差时训练完成，保存网络的权值和偏差。具体步骤如下：

　　（1）初始化，随机给定各连接权及阀值。

　　（2）由给定的输入输出模式对计算隐层、输出层各单元输出　　

　　（3）计算新的连接权及阀值，计算公式如下：

　　（4）选取下一个输入模式对返回第2步反复训练直到网络设输出误差达到要求结束训练。

　　传统的BP算法，实质上是把一组样本输入/输出问题转化为一个非线性优化问题，并通过负梯度下降算法，利用迭代运算求解权值问题的一种学习方法，但其收敛速度慢且容易陷入局部极小，为此提出了一种新的算法，即高斯消元法。

2 改进的BP网络算法

　　2．1 改进算法概述

　　此前有人提出：任意选定一组自由权，通过对传递函数建立线性方程组，解得待求权。本文在此基础上将给定的目标输出直接作为线性方程等式代数和来建立线性方程组，不再通过对传递函数求逆来计算神经元的净输出，简化了运算步骤。没有采用误差反馈原理，因此用此法训练出来的神经网络结果与传统算法是等效的。其基本思想是：由所给的输入、输出模式对通过作用于神经网络来建立线性方程组，运用高斯消元法解线性方程组来求得未知权值，而未采用传统BP网络的非线性函数误差反馈寻优的思想。

　　2．2 改进算法的具体步骤

　　对给定的样本模式对，随机选定一组自由权，作为输出层和隐含层之间固定权值，通过传递函数计算隐层的实际输出，再将输出层与隐层间的权值作为待求量，直接将目标输出作为等式的右边建立方程组来求解。

　　（1）随机给定隐层和输入层间神经元的初始权值。

　　（2）由给定的样本输入计算出隐层的实际输出。

　　（3）计算输出层与隐层间的权值。以输出层的第r个神经元为对象，由给定的输出目标值作为等式的多项式值建立方程。　 　　

    （4）重复第三步就可以求出输出层m个神经元的权值，以求的输出层的权矩阵加上随机固定的隐层与输入层的权值就等于神经网络最后训练的权矩阵。

3 计算机运算实例

  %% 清空环境变量 clc clear

%% 训练数据预测数据 data=importdata('test.txt');

%从1到768间随机排序 k=rand(1,768); [m,n]=sort(k);

%输入输出数据 input=data(:,1:8); output =data(:,9);

%随机提取500个样本为训练样本，268个样本为预测样本 input_train=input(n(1:500),:)'; output_train=output(n(1:500),:)'; input_test=input(n(501:768),:)'; output_test=output(n(501:768),:)';

%输入数据归一化 [inputn,inputps]=mapminmax(input_train);

%% BP网络训练 % %初始化网络结构 net=newff(inputn,output_train,10);

net.trainParam.epochs=1000; net.trainParam.lr=0.1; net.trainParam.goal=0.0000004;

%% 网络训练 net=train(net,inputn,output_train);

%% BP网络预测 %预测数据归一化 inputn_test=mapminmax('apply',input_test,inputps);   %网络预测输出 BPoutput=sim(net,inputn_test);

%% 结果分析 %根据网络输出找出数据属于哪类 BPoutput(find(BPoutput<0.5))=0; BPoutput(find(BPoutput>=0.5))=1;

%% 结果分析 %画出预测种类和实际种类的分类图 figure(1) plot(BPoutput,'og') hold on plot(output_test,'r*'); legend('预测类别','输出类别') title('BP网络预测分类与实际类别比对','fontsize',12) ylabel('类别标签','fontsize',12) xlabel('样本数目','fontsize',12) ylim([-0.5 1.5])

%预测正确率 rightnumber=0; for i=1:size(output_test,2)     if BPoutput(i)==output_test(i)         rightnumber=rightnumber+1;     end end rightratio=rightnumber/size(output_test,2)*100;

sprintf('测试准确率=%0.2f',rightratio)

二、遗传算法

http://blog.csdn.net/breezedust/article/details/12378031

蚁群算法之所以能引起相关领域研究者的注意，是因为这种求解模式能将问题求解的快速性、全局优化特征以及有限时间内答案的合理性结合起来。其中，寻优的快速性是通过正反馈式的信息传递和积累来保证的。而算法的早熟性收敛又可以通过其分布式计算特征加以避免，同时，具有贪婪启发

图3蚁群在障碍物前经过一段时间后的情形

式搜索特征的蚁群系统又能在搜索过程的早期找到可以接受的问题解答。这种优越的问题分布式求解模式经过相关领域研究者的关注和努力，已经在最初的算法模型基础上得到了很大的改进和拓展。

经过一定时间，从食物源返回的蚂蚁到达D点同样也碰到障碍物，也需要进行选择。此时A, B两侧的信息素浓度相同，它们仍然一半向左，一半向右。但是当A侧的蚂蚁已经完全绕过障碍物到达C点时，B侧的蚂蚁由于需走的路径更长，还不能到达C点，图3表示蚁群在障碍物前经过一段时间后的情形。

此时对于从蚁巢出发来到C点的蚂蚁来说，由于A侧的信息素浓度高，B侧的信息素较低，就倾向于选择A侧的路径。这样的结果是A侧的蚂蚁越来越多，最终所有蚂蚁都选择这条较短的路径，图4 表示蚁群最终选择的路径

图4 蚁群最终选择的路径

上述过程，很显然是由蚂蚁所留下的信息素的“正反馈”过程而导致的。蚂蚁个体就是通过这种信息的交流来达到搜索食物的目的。蚁群算法的基本思想也是从这个过程转化而来的。

遗传算法的应用
遗传算法提供了一种求解复杂系统优化问题的通用框架，它不依赖于问题的具体领域，对问题的种类有很强的鲁棒性。所以，广泛应用于很多学科。下面是遗传算法的一此主要应用领
域。
2.2.1函数优化
函数优化是遗传算法的经典应用领域，也是对遗传算法进行性能评价的常用算例。很多人构造出了各种各样的复杂形式的测试函数。有连续函数也有离散函数，有凸函数也有凹函数，有低维函数也有高维函数，有确定函数也有随机函数，有单峰值函数也有多峰值函数等。用这些几何特性各具特色的函数来评价遗传算法的性能，更能反映算法的本质效果而对于一些非线性、多模型、多目标的函数优化问题，用其他优化方法较难求解。而遗传算法却可以方便地得到较好的结果。
     
2.2.2组合优化
 随着问题规模的增大，组合优化问题的搜索空间也急剧扩大。有时在目前的计算机上用枚举法很难或甚至不可能求出其精确最优解。对这类复杂问题，人们已意识到应把主要精力放在寻求其满意解上，而遗传算法是寻求这种满意解的最佳工具之一。实践证明，遗传算法已经在求解旅行商问题、背包问题、装箱问题、布局优化、图形划分问题等各种具有NP难度的问题得到成功的应用。
2.2.3生产调度问题
生产调度问题在很多情况下建立起来的数学模难以精确求解，即使经过一些简化之后可以进行求解.也会因简化得太多而使得求解结果与实际相差甚远。目前在现实生产中主要是靠一些经验来进行调度。现在遗传算法已成为解决复杂调度问题的有效下具。在单件生产车间调度、流水线生产间调度、生产规划、任务分配等方面遗传算法都得到了有效的应用。
2.2.4自动控制
在自动控制领域中有很多与优化相关的问题需要求解。遗传算法已在其中得到了初步的应用，并显示出良好的效果。例如用遗传算法进行航空控制系统的优化、使用遗传算法设计空间交会控制器、基于遗传算法的模糊控制器的优化设计、基于遗传算法的参数辨识、基于遗传算法的模糊控制规则的学习、利用遗传算法进行人工神经网络的结构优化设计和权值学习等。都显出了遗传算法在这此领域中应用的可能性。
2.2.5 机器人学
机器人是一类复杂的难以精确建模的人工系统，而遗传算法的起源就来自于人工自适应系统的研究。所以，机器人学理所当然地成为遗传算法的一个重要应用领域。例如，遗传算法已经在移动机器人路径规划、关节机器人运动轨迹规划、机器人逆运动学求解、细胞机器人的结构优化和行为协调等方而得到研究和应用。  
2.2.6 图像处理
图像处理是计算机视觉中的一个重要研究领域。在图像处理过程中，如扫描、特征提取、图像分割等不可避免地会存在一此误差，从而影响图像的效果。如何使这些误差最小是使计算机视觉达到实用化的重要要求。遗传算法在这些图像处理中的优化计算方面找到了用武之地。目前已在模式识别(包括汉字识别)、图像恢复、图像边缘特征提取等方而得到了应用。
2.2.7 人工生命
人下生命是用计算机、机械等人下媒体模拟或构造出的具有自然生物系统特有行为的人造系统。自组织能力和自学习能力是人下生命的两大主要特征。人下生命与遗传算法有着密切的关系。基于遗传算法的进化模型是研究人下生命现象的重要基础理论。虽然人下生命的研究尚处于启蒙阶段，但遗传算法已在其进化模型、学习模型、行为模型、自组织模型等方面显示出了初步的应用能力，并且必将得到更为深入的应用和发展。人工生命与遗传算法相辅相成，遗传算法为人下生命的研究提供一个有效的下具，人下生命的研究也必将促进遗传算法的进一步发展。
2.2.8 遗传编程
1989年，美国Standford大学的Koza教授发展了遗传编程的概念,其基木思想是:采用树型结构表示计算机程序,运用遗传算法的思想,通过自动生成计算机程序来解决问题。虽然遗传编程的理论尚米成热,应用也有一此限制,但它已成功地应用于人工智能、机器学习等领域。目前公开的遗传编程实验系统有十多个。例如，Koza开发的ADF系统，While开发的GPELST系统等。
2.2.9 机器学习
学习能力是高级自适应系统所具备的能力之一，基于遗传算法的机器学习，特别是分类器系统，在很多领域中都得到了应用。例如，遗传算法被用于学习模糊控制规则，利用遗传算法来学习隶属度函数，从而更好地改进了模糊系统的性能；基于遗传算法的机器学习可用来调整人工神经网络的连接权，也可用于人工神经网络结构优化设计；分类器系统也在学习式多机器人路径规划系统中得到了成功的应用。
2.2.10 数据挖掘
数据挖掘是近几年出现的数据库技术，它能够从大型数据库中提取隐含的、先前未知的、有潜在应用价值的知识和规则。许多数据挖掘问题可看成是搜索问题，数据库看作是搜索空间，挖掘算法看作是搜索策略。因此，应用遗传算法在数据库中进行搜索，对随机产生的一组规则进行进化.直到数据库能被该组规则覆盖，从而挖掘出隐含在数据库中的规则。Sunil已成功地开发了一个基于遗传算法的数据挖掘下具。利用该工具对两个飞机失事的真实数据库进行了数据挖掘实验，结果表明遗传算法是进行数据挖掘的有效方法之一。

三、粒子群算法

 粒子群优化算法(PSO)是一种进化计算技术(evolutionary computation)，1995 年由Eberhart 博士和kennedy 博士提出，源于对鸟群捕食的行为研究 。该算法最初是受到飞鸟集群活动的规律性启发，进而利用群体智能建立的一个简化模型。粒子群算法在对动物集群活动行为观察基础上，利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解。

基本思想

    正如简介所描述的那样，粒子群算法是模拟群体智能所建立起来的一种优化算法，像后面我向大家介绍的蚁群算法也属于这类算法，粒子群算法可以用鸟类在一个空间内随机觅食为例，所有的鸟都不知道食物具体在哪里，但是他们知道大概距离多远，最简单有效的方法就是搜寻目前离食物最近的鸟的周围区域。

    所以，粒子群算法就是把鸟看成一个个粒子，并且他们拥有位置和速度这两个属性，然后根据自身已经找到的离食物最近的解和参考整个共享于整个集群中找到的最近的解去改变自己的飞行方向，最后我们会发现，整个集群大致向同一个地方聚集。而这个地方是离食物最近的区域，条件好的话就会找到食物。这就是粒子群算法，很好理解。

算法描述

    所以，我们需要一个pbest来记录个体搜索到的最优解，用gbest来记录整个群体在一次迭代中搜索到的最优解。速度和粒子位置的更新公式如下：

 

    v[i] = w * v[i] + c1 * rand() * (pbest[i] - present[i]) + c2 * rand() * (gbest - present[i])    

    present[i] = present[i] + v[i]                                                                                                          

    其中v[i]代表第i个粒子的速度，w代表惯性权值,c1和c2表示学习参数，rand()表示在0-1之间的随机数,pbest[i]代表第i个粒子搜索到的最优值,gbest代表整个集群搜索到的最优值,present[i]代表第i个粒子的当前位置。

但是粒子群算法并没有像遗传算法那样有选择交叉变异这样的过程，而更多的是体现在追踪单个粒子和共享集体最优信息来实现向最优空间搜索的形式，但是正由于它不同于遗传算法那样去忽略个体的一些内在联系，所以 往往会陷入局部最优 ，所以，在粒子群算法中 加入像遗传算法中的变异或者模拟退火等，可以跳过这个局部最优解 。

研究鸟群系统，每个鸟在这个系统中就称为主体。主体有适应性，它能够与环境及其他的主体进行交流，并且根据交流的过程“学习”或“积累经验”改变自身结构与行为。整个系统的演变或进化包括：新层次的产生（小鸟的出生）；分化和多样性的出现（鸟群中的鸟分成许多小的群）；新的主题的出现（鸟寻找食物过程中，不断发现新的食物）。

    所以CAS系统中的主体具有4个基本特点（这些特点是粒子群算法发展变化的依据）：

• 首先，主体是主动的、活动的。
• 主体与环境及其他主体是相互影响、相互作用的，这种影响是系统发展变化的主要动力。
• 环境的影响是宏观的，主体之间的影响是微观的，宏观与微观要有机结合。
• 最后，整个系统可能还要受一些随机因素的影响。

粒子群算法就是对一个CAS系统－－－鸟群社会系统的研究得出的。

       粒子群算法（ Particle Swarm Optimization, PSO）最早是由Eberhart和Kennedy于1995年提出，它的基本概念源于对鸟群觅食行为的研究。设想这样一个场景:一群鸟在随机搜寻食物，在这个区域里只有一块食物，所有的鸟都不知道食物在哪里，但是它们知道当前的位置离食物还有多远。那么找到食物的最优策略是什么呢?最简单有效的就是搜寻目前离食物最近的鸟的周围区域。   

      PSO算法就从这种生物种群行为特性中得到启发并用于求解优化问题。在PSO中，每个优化问题的潜在解都可以想象成d维搜索空间上的一个点，我们称之为“粒子”（Particle），所有的粒子都有一个被目标函数决定的适应值(Fitness Value )，每个粒子还有一个速度决定他们飞翔的方向和距离，然后粒子们就追随当前的最优粒子在解空间中搜索。Reynolds对鸟群飞行的研究发现。鸟仅仅是追踪它有限数量的邻居但最终的整体结果是整个鸟群好像在一个中心的控制之下.即复杂的全局行为是由简单规则的相互作用引起的。

不同点

与 遗传算法比较，PSO的信息共享机制是很不同的。在遗传算法中，染色体(chromosomes)互相共享信息，所以整个种群的移动是比较均匀的向最优区域移动。在PSO中, 只有gBest (orlBest) 给出信息给其他的 粒子， 这是单向的信息流动。整个搜索更新过程是跟随当前最优解的过程。与遗传算法比较, 在大多数的情况下，所有的粒子可能更快的收敛于 最优解。

四、模拟退火算法

　1. 模拟退火算法

　　2. 遗传算法

 

一. 爬山算法 ( Hill Climbing )

         介绍模拟退火前，先介绍爬山算法。爬山算法是一种简单的贪心搜索算法，该算法每次从当前解的临近解空间中选择一个最优解作为当前解，直到达到一个局部最优解。

         爬山算法实现很简单，其主要缺点是会陷入局部最优解，而不一定能搜索到全局最优解。如图1所示：假设C点为当前解，爬山算法搜索到A点这个局部最优解就会停止搜索，因为在A点无论向那个方向小幅度移动都不能得到更优的解。

图1

 

 

二. 模拟退火(SA,Simulated Annealing)思想

         爬山法是完完全全的贪心法，每次都鼠目寸光的选择一个当前最优解，因此只能搜索到局部的最优值。模拟退火其实也是一种贪心算法，但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。以图1为例，模拟退火算法在搜索到局部最优解A后，会以一定的概率接受到E的移动。也许经过几次这样的不是局部最优的移动后会到达D点，于是就跳出了局部最大值A。

         模拟退火算法描述：

         若J( Y(i+1) )>= J( Y(i) )  (即移动后得到更优解)，则总是接受该移动

         若J( Y(i+1) )< J( Y(i) )  (即移动后的解比当前解要差)，则以一定的概率接受移动，而且这个概率随着时间推移逐渐降低（逐渐降低才能趋向稳定）

　　这里的“一定的概率”的计算参考了金属冶炼的退火过程，这也是模拟退火算法名称的由来。

　　根据热力学的原理，在温度为T时，出现能量差为dE的降温的概率为P(dE)，表示为：

　　　　P(dE) = exp( dE/(kT) )

　　其中k是一个常数，exp表示自然指数，且dE<0。这条公式说白了就是：温度越高，出现一次能量差为dE的降温的概率就越大；温度越低，则出现降温的概率就越小。又由于dE总是小于0（否则就不叫退火了），因此dE/kT < 0 ，所以P(dE)的函数取值范围是(0,1) 。

　　随着温度T的降低，P(dE)会逐渐降低。

　　我们将一次向较差解的移动看做一次温度跳变过程，我们以概率P(dE)来接受这样的移动。

　　关于爬山算法与模拟退火，有一个有趣的比喻：

　　爬山算法：兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法，它不能保证局部最优值就是全局最优值。

　　模拟退火：兔子喝醉了。它随机地跳了很长时间。这期间，它可能走向高处，也可能踏入平地。但是，它渐渐清醒了并朝最高方向跳去。这就是模拟退火。

 

下面给出模拟退火的伪代码表示。

 

三. 模拟退火算法伪代码

代码

/* * J(y)：在状态y时的评价函数值 * Y(i)：表示当前状态 * Y(i+1)：表示新的状态 * r： 用于控制降温的快慢 * T： 系统的温度，系统初始应该要处于一个高温的状态 * T_min ：温度的下限，若温度T达到T_min，则停止搜索 */ while( T > T_min ) { 　　dE = J( Y(i+1) ) - J( Y(i) ) ;  　　if ( dE >=0 ) //表达移动后得到更优解，则总是接受移动 Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动 　　else 　　{ // 函数exp( dE/T )的取值范围是(0,1) ，dE/T越大，则exp( dE/T )也 if ( exp( dE/T ) > random( 0 , 1 ) ) Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动 　　} 　　T = r * T ; //降温退火 ，0 　　/* 　　* 若r过大，则搜索到全局最优解的可能会较高，但搜索的过程也就较长。若r过小，则搜索的过程会很快，但最终可能会达到一个局部最优值 　　*/ 　　i ++ ; }

四. 使用模拟退火算法解决旅行商问题

　　旅行商问题 ( TSP , Traveling Salesman Problem ) ：有N个城市，要求从其中某个问题出发，唯一遍历所有城市，再回到出发的城市，求最短的路线。

　　旅行商问题属于所谓的NP完全问题，精确的解决TSP只能通过穷举所有的路径组合，其时间复杂度是O(N!) 。

　　使用模拟退火算法可以比较快的求出TSP的一条近似最优路径。（使用遗传算法也是可以的，我将在下一篇文章中介绍）模拟退火解决TSP的思路：

1. 产生一条新的遍历路径P(i+1)，计算路径P(i+1)的长度L( P(i+1) )

2. 若L(P(i+1)) < L(P(i))，则接受P(i+1)为新的路径，否则以模拟退火的那个概率接受P(i+1) ，然后降温

3. 重复步骤1，2直到满足退出条件

　　产生新的遍历路径的方法有很多，下面列举其中3种：

1. 随机选择2个节点，交换路径中的这2个节点的顺序。

2. 随机选择2个节点，将路径中这2个节点间的节点顺序逆转。

3. 随机选择3个节点m，n，k，然后将节点m与n间的节点移位到节点k后面。

 

五. 算法评价

        模拟退火算法是一种随机算法，并不一定能找到全局的最优解，可以比较快的找到问题的近似最优解。 如果参数设置得当，模拟退火算法搜索效率比穷举法要高。