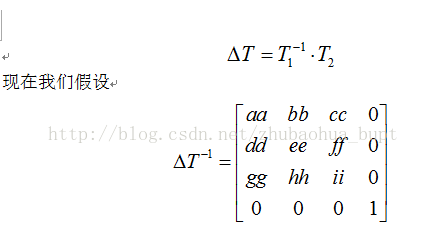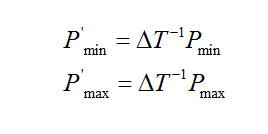转载请说明出处:
http://blog.csdn.net/zhubaohua_bupt/article/details/54093689
最近利用单目相机在做三维重建相关的工作,下面总结一下摄像机运动对单目深度估计的影响。
单目方法求取深度的一般流程是
1设定待求取区域
2根据帧间位姿和带有误差的深度计算像素在后来帧上的极线
3在极线上寻找匹配
4三角测量求出本次的观测深度值以及深度的不确定性
5多次测量的深度数据以及方差融合
6 去噪平滑深度图
下面看一下相机的运动会对深度估计带来哪些影响。
对以下文章的符号说明:
T:相机相对于世界坐标系的位姿 大小4*4
e:极点 (二维像素平面坐标)
o:相机光心
f:像素点在当前相机坐标系下的单位方向向量 (三维)
d:像素深度
p(u,v):像素平面坐标
P(X,Y,Z):相机坐标系下的三维坐标
t:图像平面或时间
一:纯平移对匹配搜索极线的影响
在平移不至于丢失共同视野的情况下,平移越大,匹配搜索极线越长。
如下两幅图
小平移
大平移
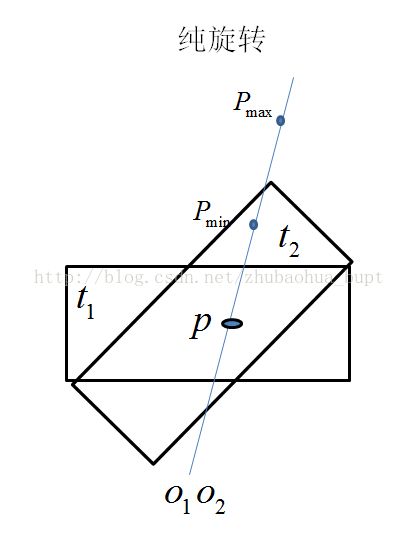
二:纯旋转对深度估计的影响
从几何直观来看:
我们求取深度的时候第2步要计算在后帧上的极线,纯旋转情况下,由于我们无法得到极线,因此也就无法匹配、三角测量求取深度。
理论证明:
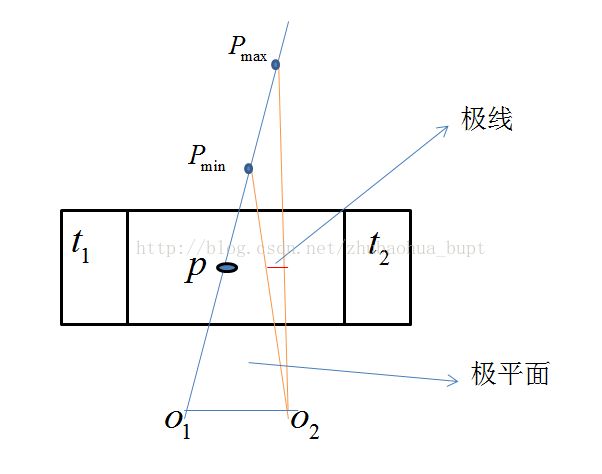
t1和t2为两个时刻对应的图像平面,现在我们想利用t2时刻相机拍摄到的图像来求取t1时刻上像素的深度。
假设:t1时刻的相机坐标系为世界坐标系,t2时刻的相机坐标系为t1时刻的相机坐标系纯旋转得到。
那么t2时刻,相机相对于t1时刻的位姿为:
接下来,我们试图计算t1时刻相机图像平面上的p点在t2时刻相机平面上的极线
p点的最小深度为dmin,最大深度为dmax,f为p点在t1时刻相机坐标系下的单位空间方向向量,使得
这里Pmin和Pmax同在一条由t1时刻光心发出的一条射线上。
现在我们利用位姿把Pmin和Pmax转换至t2相机坐标系下,其坐标分别记作P’min和P'max
那么问题就来了,我们本打算利用位姿把Pmin和Pmax转换至t2相机坐标系下,然后通过内参求出在t2时刻图像上对应的极点emax,emin。
但是现在P'min和P'max成比例,也就是说:
这两个点在t2相机坐标系下表示的三维点处在t2光心发出的某一条射线上,即它们对应的极点e(这里应该不能称为极点了吧。。)是同一个,因此也就无法计算极线。
结论:单目相机在纯旋转的情况下无法计算深度。
欢迎大家纠错与补充,一起进步。