首发地址:https://www.fmz.com/digest-topic/4035
1.简单介绍
深度神经网络这些年越来越热门,在很多领域解决了过去无法解决的难题,体现了强大的能力。在时间序列的预测上,常用的神经网络价格是RNN,因为RNN不仅有当前数据输入,还有历史数据的输入,当然,当我们谈论RNN预测价格时,往往谈论的是RNN的一种:LSTM。本文就将以pytorch为基础,构建预测比特币价格的模型。网上相关的资料虽然多,但还是不够透彻,使用pytorch的也相对较少,还是有必要写一篇文章, 最终结果是利用比特币行情的开盘价、收盘价、最高价、最低价、交易量来预测下一个收盘价。我个人神经网络知识一般,欢迎各位大佬批评指正。
本教程由FMZ发明者数字货币量化交易平台出品(www.fmz.com),欢迎入QQ群:863946592 交流。
2.数据和参考
比特币价格数据来源自FMZ发明者量化交易平台:https://www.quantinfo.com/Tools/View/4.html
一个相关的价格预测例子:https://yq.aliyun.com/articles/538484
关于RNN模型的详细介绍:https://zhuanlan.zhihu.com/p/27485750
理解RNN的输入输出:https://www.zhihu.com/question/41949741/answer/318771336
关于pytorch:官方文档 https://pytorch.org/docs 其它资料自行搜索吧。
另外读懂本文还需要一些前置知识,如pandas/爬虫/数据处理等,但不会也没关系。
3.pytorch LSTM模型的参数
LSTM的参数:
第一次看到文档上这些密密麻麻的参数,我的反应是:
随着慢慢阅读,总算大概明白了
input_size: 输入向量x的特征大小,如果以收盘价预测收盘价,那么input_size=1;如果以高开低收预测收盘价,那么input_size=4hidden_size: 隐含层大小num_layers: RNN的层数batch_first: 如果为True则输入维度的第一个为batch_size,这个参数也很让人困惑,下面将详细介绍。
输入数据参数:
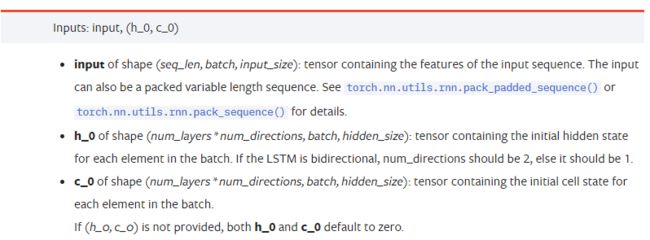
input: 具体输入的数据,是一个三维的tensor, 具体的形状为:(seq_len, batch, input_size)。其中,seq_len指序列的长度,即LSTM需要考虑多长时间的历史数据,注意这个指只是数据的格式,不是LSTM内部的结构,同一个LSTM模型可以输入不同seq_len的数据,都能给出预测的结果;batch指batch的大小,代表有多少组不同的数据;input_size就是前面的input_size。h_0: 初始的hidden状态, 形状为(num_layers * num_directions, batch, hidden_size),如果时双向网络num_directions=2c_0: 初始的cell状态, 形状同上, 可以不指定。
输出参数:
output: 输出的形状 (seq_len, batch, num_directions * hidden_size),注意和模型参数batch_first有关h_n: t = seq_len时刻的h状态,形状同h_0c_n: t = seq_len时刻的c状态,形状同c_0
4.LSTM输入输出的简单例子
首先导入所需要的包
import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
定义LSTM模型
LSTM = nn.LSTM(input_size=5, hidden_size=10, num_layers=2, batch_first=True)
准备输入的数据
x = torch.randn(3,4,5) # x的值为: tensor([[[ 0.4657, 1.4398, -0.3479, 0.2685, 1.6903], [ 1.0738, 0.6283, -1.3682, -0.1002, -1.7200], [ 0.2836, 0.3013, -0.3373, -0.3271, 0.0375], [-0.8852, 1.8098, -1.7099, -0.5992, -0.1143]], [[ 0.6970, 0.6124, -0.1679, 0.8537, -0.1116], [ 0.1997, -0.1041, -0.4871, 0.8724, 1.2750], [ 1.9647, -0.3489, 0.7340, 1.3713, 0.3762], [ 0.4603, -1.6203, -0.6294, -0.1459, -0.0317]], [[-0.5309, 0.1540, -0.4613, -0.6425, -0.1957], [-1.9796, -0.1186, -0.2930, -0.2619, -0.4039], [-0.4453, 0.1987, -1.0775, 1.3212, 1.3577], [-0.5488, 0.6669, -0.2151, 0.9337, -1.1805]]])
x的形状为(3,4,5),由于我们之前定义了batch_first=True, 此时的batch_size的大小为3, sqe_len为4, input_size为5。 x[0]代表了第一个batch。
如果没定义batch_first,默认为False,则此时数据的代表的完全不同,batch大小为4, sqe_len为3, input_size为5。 此时x[0]代表了所有batch在t=0时数据,依次类推。 个人感觉这种设定不符合直觉, 所以添加了参数batch_first=True.
两者之间数据的转换也很方便: x.permute(1,0,2)
输入和输出
LSTM的输入输出的形状很容易让人迷惑,借助下图可以辅助理解:
来源:https://www.zhihu.com/question/41949741/answer/318771336
x = torch.randn(3,4,5) h0 = torch.randn(2, 3, 10) c0 = torch.randn(2, 3, 10) output, (hn, cn) = LSTM(x, (h0, c0)) print(output.size()) #在这里思考一下,如果batch_first=False输出的大小会是多少? print(hn.size()) print(cn.size()) #结果 torch.Size([3, 4, 10]) torch.Size([2, 3, 10]) torch.Size([2, 3, 10])
观察输出的结果,和前面的参数的解释一致.注意到hn.size()的第二个值为3,和batch_size的大小保持一致,说明hn中并没有保存中间状态,只保存了最后一步。
由于我们的LSTM网络有两层,其实hn最后一层的输出就是output的值,output的形状为[3, 4, 10],保存了t=0,1,2,3所有时刻的结果,所以:
hn[-1][0] == output[0][-1] #第一个batch在hn最后一层的输出等于第一个batch在t=3时output的结果 hn[-1][1] == output[1][-1] hn[-1][2] == output[2][-1] 5.准备比特币行情数据
前面讲了这么多内容,只是铺垫,理解LSTM的输入输出很是重要,否则随意从网上摘抄一些代码很容易出错,由于LSTM在时间序列上的强大能力,即使模型是错误的,最后也能得出的不错结果。
数据的获取
数据使用的是Bitfinex交易所BTC_USD交易对的行情数据。
import requests import json resp = requests.get('https://www.quantinfo.com/API/m/chart/history?symbol=BTC_USD_BITFINEX&resolution=60&from=1525622626&to=1562658565') data = resp.json() df = pd.DataFrame(data,columns = ['t','o','h','l','c','v']) print(df.head(5))
数据格式如下:
数据的预处理
df.index = df['t'] # index设为时间戳 df = (df-df.mean())/df.std() # 数据的标准化,否则模型的Loss会非常大,不利于收敛 df['n'] = df['c'].shift(-1) # n为下一个周期的收盘价,是我们预测的目标 df = df.dropna() df = df.astype(np.float32) # 改变下数据格式适应pytorch
数据的标准化的方法非常粗糙,会有一些问题,仅仅是演示,可以使用收益率之类的数据标准化。
准备训练数据
seq_len = 10 # 输入10个周期的数据 train_size = 800 # 训练集batch_size def create_dataset(data, seq_len): dataX, dataY=[], [] for i in range(0,len(data)-seq_len, seq_len): dataX.append(data[['o','h','l','c','v']][i:i+seq_len].values) dataY.append(data['n'][i:i+seq_len].values) return np.array(dataX), np.array(dataY) data_X, data_Y = create_dataset(df, seq_len) train_x = torch.from_numpy(data_X[:train_size].reshape(-1,seq_len,5)) #变化形状,-1代表的值会自动计算 train_y = torch.from_numpy(data_Y[:train_size].reshape(-1,seq_len,1))
最终train_x和train_y的形状分别为:torch.Size([800, 10, 5]), torch.Size([800, 10, 1])。 由于我们的模型是根据10个周期的数据预测下个周期的收盘价,理论上800个batch,只要有800个预测收盘价就行了。但train_y在每个batch中有10个数据,实际上每个batch预测的中间结果是保留的,并不只有最后一个。在计算最后的Loss时,可以把所有的10个预测结果都考虑进去和train_y中实际值进行比较。 理论上也可以只计算最后一个预测结果的Loss。画了一个粗糙的图说明这个问题。由于LSTM的模型实际不包含seq_len参数,所以模型可适用不同的长度,中间的预测结果也是有意义的,因此我倾向于合并计算Loss。
注意在准备训练数据时,窗口的移动是跳跃的,已经使用的数据不再使用,当然窗口也可以逐个移动,这样得到的训练集会大很多。但感觉这样相邻的batch数据太重复了,于是采用了当前方法。
6.构造LSTM模型
最终构建的模型如下, 包含一个两层的LSTM, 一个Linear层。
class LSTM(nn.Module): def __init__(self, input_size, hidden_size, output_size=1, num_layers=2): super(LSTM, self).__init__() self.rnn = nn.LSTM(input_size,hidden_size,num_layers,batch_first=True) self.reg = nn.Linear(hidden_size,output_size) # 线性层,把LSTM的结果输出成一个值 def forward(self, x): x, _ = self.rnn(x) # 如果不理解前向传播中数据维度的变化,可单独调试 x = self.reg(x) return x net = LSTM(5, 10) # input_size为5,代表了高开低收和交易量. 隐含层为10.
7.开始训练模型
终于开始训练了,代码如下:
criterion = nn.MSELoss() # 使用了简单的均方差损失函数 optimizer = torch.optim.Adam(net.parameters(),lr=0.01) # 优化函数,lr可调 for epoch in range(600): # 由于速度很快,这里的epoch多一些 out = net(train_x) # 由于数据量很小, 直接拿全量数据计算 loss = criterion(out, train_y) optimizer.zero_grad() loss.backward() # 反向传播损失 optimizer.step() # 更新参数 print('Epoch: {:<3}, Loss:{:.6f}'.format(epoch+1, loss.item()))
训练结果如下:
8.模型评价
模型的预测值:
p = net(torch.from_numpy(data_X))[:,-1,0] # 这里只取最后一个预测值作为比较 plt.figure(figsize=(12,8)) plt.plot(p.data.numpy(), label= 'predict') plt.plot(data_Y[:,-1], label = 'real') plt.legend() plt.show()
根据图上可以看出,训练数据(800之前)的吻合度非常高,但后期比特币价格上涨新高,模型未见过这些数据,预测就力不从心了。这也说明了前面数据标准化时有问题。
虽然预测的价格不一定准确,那么预测涨跌的准确率如何呢?截取一段预测数据看一下:
r = data_Y[:,-1][800:1000] y = p.data.numpy()[800:1000] r_change = np.array([1 if i > 0 else 0 for i in r[1:200] - r[:199]]) y_change = np.array([1 if i > 0 else 0 for i in y[1:200] - y[:199]]) print((r_change == y_change).sum()/float(len(r_change)))
结果预测涨跌的准确率达到了77.4%,还是超出我的预期。不知道是不是哪里搞错了
当然此模型没有什么实盘价值,但简单易懂,仅依此入门,接下来还会有更多的神经网络入门应用在数字货币量化的入门课程。