科研篇二:对抗样本(Adversarial Example)综述
文章目录
- 一、写作动机与文献来源
- 二、术语定义
- 2.1.对抗样本/图片(Adversarial Example/Image)
- 2.2.对抗干扰(Adversarial perturbation)
- 2.3.对抗训练(Adversarial Training)
- 2.4.对抗方(Adversary)
- 2.5.黑盒攻击(Black-box attacks)
- 2.6.探测器(Detector)
- 2.7. 愚弄率(Fooling ratio/rate)
- 2.8.单步方法(one-shot/one-step methods)
- 2.9.外观不可感知的(Quasi-imperceptible)
- 2.10.修正器(Rectifier)
- 2.11.有目标攻击(Targeted attacks)
- 2.12.威胁模型(Threat model)
- 2.13.迁移性(Transferability)
- 2.14.通用干扰(Universal perturbation)
- 2.15. 白盒攻击(White-box attacks)
- 三、对抗攻击(Adversarial Attacks)
- 3.1. 针对分类的攻击
- 3.1.1. Box-constrained L-BFGS
- 3.1.2.Fast Gradient Sign Method(FGSM)
- 3.1.6.Carlini and Wagner Attacks(C&W)
- 四、对抗防御(Adversatrial Defence)
- 4.1 修改输入/训练 Modified training / input
- 4.1.1暴力的对抗训练
- 4.1.2 基于数据压缩做防御
- END.Reference
一、写作动机与文献来源
- paper:Threat of Adversarial Attacks on Deep Learning in Computer Vision: A Survey
- 写作动机:对抗攻击入门
- 说明:本文是2018年左右的一篇综述,现在很多最新的进展没有被包含在内。但是涵盖了最经典的一些对抗攻击与防御方法。推荐作为该方向的入门读物。
二、术语定义
在本节,我们将对计算机视觉中深度学习相关的对抗攻击的属于进行描述。
2.1.对抗样本/图片(Adversarial Example/Image)
对抗样本/图片指的是在对干净的图片(clean image)有意图地加上噪声干扰以达到愚弄机器学习技术(比如深度神经网络)的目的的修改版本。
2.2.对抗干扰(Adversarial perturbation)
使得原始图片成为对抗样本所需要添加的噪声
2.3.对抗训练(Adversarial Training)
除了原始图片样本之外还使用到对抗样本作为训练数据的一种训练方式
2.4.对抗方(Adversary)
广泛地来说,对抗方指的是产生对抗样本的代理(agent)。然而,有的时候对抗样本本身也被称作对抗方。
2.5.黑盒攻击(Black-box attacks)
不知道被攻击模型的具体细节,称之为黑盒攻击。在一些情况下,也会假设对抗方对模型有十分有限的了解(比如:模型的训练过程和/或其结构),但是绝对不知道模型的参数。在另外的一些情况下,使用到任何与目标模型相关的信息都被认为是 半黑盒攻击(semi-black-box attack)。在本文中,我们采用前一种定义。
2.6.探测器(Detector)
探测器用来判断一张图片是否是对抗样本
2.7. 愚弄率(Fooling ratio/rate)
愚弄率指的是一个被训练过的模型在图片被干扰之后改变其原本预测的类别的比例。
2.8.单步方法(one-shot/one-step methods)
单步方法通过执行单步计算来产生对抗干扰,比如:计算一次模型的loss的梯度。与之对应的是迭代方法,这类方法为了得到一次扰动需要多次执行相同的计算。迭代方法毫无疑问在计算代价上是十分昂贵的。
2.9.外观不可感知的(Quasi-imperceptible)
对抗样本引入的干扰可以微小到不被人类感知。
2.10.修正器(Rectifier)
修正器会将对抗样本在特定模型上的预测结果修正成与原始样本的预测结果一致。
2.11.有目标攻击(Targeted attacks)
有目标攻击会让模型将对抗样本错误地分成某种特定的类别。与之相对的是无目标攻击。无目标攻击的目的相对简单,它只追求让模型分错,并不追求到分成何种类型。
2.12.威胁模型(Threat model)
威胁模型指的是被一种方法所考虑到的潜在的攻击。(比如:黑盒攻击)
2.13.迁移性(Transferability)
迁移性指的是对抗样本即便在攻击其他模型(指的是不是用来生成该对抗样本的模型)时仍能够保持其有效的一种品质。
2.14.通用干扰(Universal perturbation)
通用干扰能够在任意的图片上愚弄到模型。需要指出的是:通用性指的是干扰在对“图像没有任何知识”的情况下的性质,与之前提到的迁移性是不一样的。
2.15. 白盒攻击(White-box attacks)
三、对抗攻击(Adversarial Attacks)
本节将按照时间顺序来对相关技术进行介绍。对于核心的概念和代表性的技术,我们将进行详细的介绍,其余则略之。
本节可以分成两个部分。
- 3.1:主要讨论攻击计算机视觉中最常见的任务(即:分类/识别)的方法
- 3.2:主要讨论除了分类任务之外的一些其他task上的攻击方法
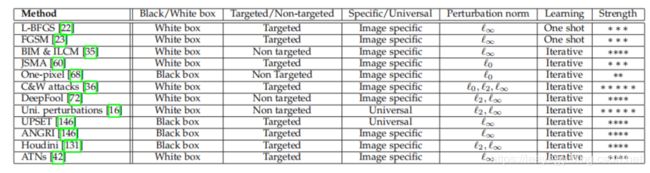
在具体地介绍这些攻击方法之前,先放上一张总结的图片,读者可以直接根据需求定位到感兴趣的攻击方法:
3.1. 针对分类的攻击
3.1.1. Box-constrained L-BFGS
背景
Szegedy[1] 等人第一次介绍了对抗样本的存在来让模型错分类。
数学表达
令 I c ∈ R m I_c\in \mathbb{R}^m Ic∈Rm代表向量化之后的原始图片,下标 c c c强调的样本是原始样本(clean image)。为了计算一个额外的扰动 ρ ∈ R m \rho\in\mathbb{R}^m ρ∈Rm,该扰动轻微地扰动图片来达到愚弄网络的目的,这些学者提出要解决下面的问题:
min ρ ∣ ∣ ρ ∣ ∣ 2 s . t . C ( I c + ρ ) = l , I c + ρ ∈ [ 0 , 1 ] m \min \limits_{\rho} \vert\vert\rho\vert\vert_2 \\ s.t. \quad C(I_c+\rho)=l,I_c+\rho\in[0,1]^m ρmin∣∣ρ∣∣2s.t.C(Ic+ρ)=l,Ic+ρ∈[0,1]m
其中, l l l代表图片的类别,C代表深度神经网络分类器。作者提出要解决该问题,为了让其有意义, l l l需要与其原始样本的类别不一致。在这种情况下,使用Box-contrained L-BFGS来作为一个近似解。这可以通过找到一个最小的正常数c在满足条件 C ( I c + ρ ) = l C(I_c+\rho)=l C(Ic+ρ)=l的前提下最小化 ρ \rho ρ来做到,见下式:
min ρ c ∣ ρ ∣ + L ( I c + ρ , l ) s . t . I c + ρ ∈ [ 0 , 1 ] m \min\limits_{\rho}c\vert \rho\vert+L(I_c+\rho,l) \quad s.t.I_c+\rho \in[0,1]^m ρminc∣ρ∣+L(Ic+ρ,l)s.t.Ic+ρ∈[0,1]m
上式中的L计算分类器的损失值。
3.1.2.Fast Gradient Sign Method(FGSM)
在这里需要介绍到三个团队的工作。
1.Goodfellow et al.
Szegedy[1] 等人发现深度神经网络在对抗样本上的健壮性可以通过对抗训练来提高。Goodfellow[2]等人提出一种针对给定的图片有效地计算对抗扰动的方法:
ρ = ϵ s i g n ( ∇ J ( θ , I c , l ) ) \rho=\epsilon sign(\nabla J(\theta,I_c,l)) ρ=ϵsign(∇J(θ,Ic,l))
其中, ∇ J ( . . . ) \nabla J(...) ∇J(...)计算损失函数的梯度,sign代表符号函数, ϵ \epsilon ϵ代表的是一个很小标量值,用以限制扰动的范数值。求解该问题的方法就被术语化为“FGSM”。
需要提到的是,在这篇论文中,其作者假设现代的深度神经网络都鼓励计算收益时的线性行为,这也使得容易受到廉价分析干扰的影响。在之后的文献,这被称作是“线性假设(linearity hypothesis)”
2.Kurakin et al.
Kurakin[3]等人在ImageNet进行了具体的实验,他们提出了一个单步目标类别(one-step target class)的FGSM的变体,在这个变体中,使用的不是图片的真实标签而是使用网络对原始样本 I c I_c Ic所预测的最不可能类别作为目标标签 l t a r g e t l_{target} ltarget。
他们的工作表明:一个任意的类别都可以作为愚弄网络的目标类别。
3.Miyato et al.
Miyato[4]等人提出了一个非常类似的计算方法:
ρ = ϵ ∇ J ( θ , I c , l ) ∥ ∇ J ( θ , I c , l ) ∥ 2 \rho=\epsilon \frac{\nabla J(\theta,I_c,l)}{\Vert\nabla J(\theta,I_c,l)\Vert}_2 ρ=ϵ∥∇J(θ,Ic,l)∥∇J(θ,Ic,l)2
在上面的方程中,计算的梯度被L2范数正则化。Kurakin等人[3]把这个技术叫做“Fast Gradient L2”,并且也提了一种使用无穷范数进行正则化的版本,并且命名为:“Fast Gradient L ∞ L_{\infty} L∞”。
总的来说,所有的这些方法都被视作“one-step”或者“one-shot”方法。
3.1.6.Carlini and Wagner Attacks(C&W)
Carlini和Wagner[5]在蒸馏防御[6]之后提出了三个对抗攻击方法。他们的工作表明:针对特定网络的防御蒸馏在这些攻击面前都失败了。
四、对抗防御(Adversatrial Defence)
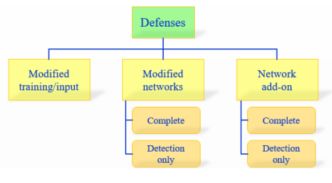
现在的对抗防御方法的思路大致可以分成一下三类:
| 序号 | 关键词 | 详细描述 | 思路分析 |
|---|---|---|---|
| 1 | 修改输入/修改训练 | 在学习的过程中使用modified training;或者是在测试的过程中使用修改过的输入modefied input | 有没有可能通过数据处理的方式破坏掉对抗扰动? |
| 2 | 修改网络 | 修改网络,比如:①增加新的layer ②增加新的子网络 ③修改损失函数loss_function ④修改激活函数 | 从造成网络脆弱性的原因出发:是不是因为当前采用的loss_function造成了脆弱性呢?这其实是在探索造成output对于input敏感性大的原因所在 |
| 3 | network add-on | 在对样本进行分类的时候使用一个外包部的模型作为一个附加的网络 | – |
在图1中的又将后两类做了分类:
| 类别 | 描述 |
|---|---|
| complete defence | 使得网络能够提升对待对抗样本的鲁棒性 |
| detection only | 此类网络的做法就是发现潜在的对抗样本输入,对于这样的样本拒绝作出进一步的处理。 |
4.1 修改输入/训练 Modified training / input
4.1.1暴力的对抗训练
原理概述
对抗训练本质上是一个min-max问题:
min θ 1 n ∑ i = 1 n max ∥ x i − x i 0 ∥ p ≤ ϵ l o s s ( h θ ( x i ) , y i ) \mathop{\min}\limits_\theta \frac{1}{n} \sum_{i=1}^{n} \mathop{\max}\limits_{\Vert x_i -x_i^0\Vert_p\leq\epsilon}loss(h_\theta(x_i),y_i) θminn1i=1∑n∥xi−xi0∥p≤ϵmaxloss(hθ(xi),yi)
内部是一个max问题,该过程希望找到一个使得当前loss最大的对抗样本(在约束的 b a l l − ϵ ball-\epsilon ball−ϵ范围内)。
外部是一个min问题,min的对象仍旧是loss,也就是说对抗训练希望对于能找到的最强的对抗样本下仍然表现不错(min loss体现了这一理念)。这个max、min问题并没有解析解,很多情况下对抗训练的性能取决于max问题的求解情况。
论文建议阅读
| 论文 | 概述 | 发表 |
|---|---|---|
| Adversarial Training Methods for Semi-Supervised Text Classification | 提出一种virtual adv_training来讲监督学习上的算法扩展到半监督学习。该方法主要被扩展到文本领域,应对稀疏高维的输入,比如独热模式的word embedding | ICLR17 |
| Improving the robustness of deep neural networks via stability training | 应对压缩、rescaling、cropping带来的微小扰动对模型输出效果的显著影响问题,并不是直接针对对抗样本;注意与数据增强训练是有区别的。 | CVPR16 |
需要注意的是:对抗训练往往需要更大的训练数据,因此训练代价就会增大。同时,对抗训练的迁移性并不强,针对某一类攻击方法生成的样本进行的对抗训练往往在不同攻击类型的鲁棒性上的表现不佳。
4.1.2 基于数据压缩做防御
END.Reference
[1]C. Szegedy, W. Zaremba, I. Sutskever, J. Bruna, D. Erhan, I.
Goodfellow, R. Fergus, Intriguing properties of neural networks, arXiv
preprint arXiv:1312.6199, 2014.
[2]