Concurrent Spatial and Channel ‘Squeeze & Excitation’ in Fully Convolutional Networks(附代码)
文章目录
- 摘要
- 介绍
- 方法
- 空间压缩和信道激励(cSE)
- 通道压缩和空间激励
- 空间和通道的压缩和激励模块(scSE)
- 模型复杂性
摘要
全卷积网络为大量应用设置了图像分割的最新技术,F-CNN中的结构创新集中在空间编码或网络连接来帮助梯度流。本文,探索了一种自适应地重新校准特征图的方向,来增加有意义的特征,同时抑制弱的特征。我们从最近提出的squeeze & excitation(SE)模块获得灵感,该模块是用于图像分类特征图的通道重新校准。为此,我们介绍了用于图像分割的三种SE模块变体:
- 压缩空间和激励信道(cSE)
- 压缩信道和激励空间(sSE)
- 并行的空间和信道压缩和激励(scSE)
我们有效的将这些SE模块整合到DenseNet, SD-Net, U-Net框架中,并观察性能的持续改进,同时最小化对模型复杂性的影响。对两个具有挑战性的应用进行了评估:MRI扫描上的全脑分割和全身增强CT扫描上的器官分割。
介绍
卷积网络已经成为图像分类的标准方式,全卷机已经成为许多图像分类任务的首先工具。这些架构的基础是卷积层,通过过滤器对所有输入channel捕捉局部空间特征,并生成共同编码空间和通道信息的特征图。虽然对空间信息和通道信息的联合编码进行了大量的改进,但对空间模式和通道模式的独立编码探索却较少。最近的工作试图通过明确建模特征映射通道间的相互依赖性来解决上述问题,介绍了一种称为SE的模块,它可以无缝集成到任何一个CNN模型中。
SE模块通过全局平均池排除空间依赖性,来学习特定于通道的描述符,该描述符用于重新校准功能图,强调有用的通道。SE沿空间域挤压,并沿通道激励或重新加权。一个带有SE块的卷积网络在ILSVRC 2017年图像网数据集分类竞争中获得第一名,表明其有效性。
在这项工作中,我们希望利用SE块的高性能对F-CNN图像进行分类。我们将前面介绍的SE块称为信道SE(CSE),因为它只激励信道方向,这对分类是有效的。我们假设,对于图像分割,像素空间信息更具信息性。因此,我们引入另一个SE块,它沿着通道“挤压”并在空间上“激发”,称为空间SE(SSE)。最后,我们提出了并行空间和信道SE块(SCSE),分别沿信道和空间重新校准特征映射,然后结合输出。激发特征图在空间和渠道上的更多信息。
方法
如图1(a)所示,通过将SE块放在每个编码器(池化层)和解码器块(上采样层)之后,可以无缝集成到任何F-CNN模型中。

空间压缩和信道激励(cSE)
压缩空间通过全局平均池化层,产生一个z向量(1x1xC),然后通过一个全连接层和激活层(RELU),再通过一个全连接层。这对通道依赖项进行了编码。
![]()
然后通过sigmoid层获取激活值使其介于[0,1],并用于激励或重新校准通道内的值。激活值可以表示重要的通道并忽略不重要的通道。

def cse_block(prevlayer, prefix):
mean = Lambda(lambda xin: K.mean(xin, axis=[1, 2]))(prevlayer) # H W 求均值
# K.int_shape() Returns the shape of tensor or variable as a tuple of int or None entries
lin1 = Dense(K.int_shape(prevlayer)[3] // 2, name=prefix + 'cse_lin1', activation='relu')(mean)
lin2 = Dense(K.int_shape(prevlayer)[3], name=prefix + 'cse_lin2', activation='sigmoid')(lin1)
x = Multiply()([prevlayer, lin2])
return x
通道压缩和空间激励
该SE模块在通道挤压和空间激励,对于细粒度图像分割具有重要意义。
操作,文中将输入看做U,每个 u i , j u^{i,j} ui,j维度为(1,1,C),然后通过一个卷积 q = W s q ∗ U , W s q 属 于 ( 1 , 1 , C , 1 ) , q 属 于 ( H , W ) q=W_{sq}*U,W_{sq}属于(1,1,C,1),q属于(H,W) q=Wsq∗U,Wsq属于(1,1,C,1),q属于(H,W),这里生成的结果q可以理解,而生成q的方式应该是将卷积作为一种全连接的方式。
![]()
将获取的q通过sigmoid激活,生成的[0,1],参与每个位置的计算。
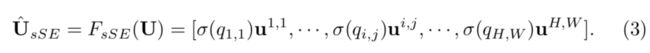
关于这个操作我是有疑问的,所以将原文贴到这里,也希望看懂的可以评论解惑。

附上找到的代码,同样有疑惑,但代码的参数个数与论文一致,结果的维度并不一致。
def sse_block(prevlayer, prefix):
# Bug? Should be 1 here?
conv = Conv2D(K.int_shape(prevlayer)[3], (1, 1), padding="same", kernel_initializer="he_normal",
activation='sigmoid', strides=(1, 1),
name=prefix + "_conv")(prevlayer)
conv = Multiply(name=prefix + "_mul")([prevlayer, conv])
return conv
最后附上自己理解的
def sse_block(prevlayer, prefix):
# Bug? Should be 1 here?
conv = Conv2D(1, (1, 1), padding="valid", kernel_initializer="he_normal",
activation='sigmoid', strides=(1, 1),
name=prefix + "_conv")(prevlayer)
conv = Multiply(name=prefix + "_mul")([prevlayer, conv])
return conv
q的每一个激活值与所给特征地图的空间信息相关,这种再校准提供了更多的权重到相关的空间信息,忽略了不相关的空间信息
空间和通道的压缩和激励模块(scSE)
def csse_block(x, prefix):
cse = cse_block(x, prefix)
sse = sse_block(x, prefix)
x = Add(name=prefix + "_csse_mul")([cse, sse])
return x
模型复杂性
cSE模块有 C 2 C^2 C2个参数,sCE有 C C C个参数,因而一个block的参数就是 C 2 + C C^2+C C2+C个参数。以一个例子来看U-net模型有 2.1 ∗ 1 0 6 2.1*10^6 2.1∗106个参数,scSE模块添加了 3.3 ∗ 1 0 4 3.3*10^4 3.3∗104个参数,增加了约1.5%,可以看出SE模块增加了很小的模型复杂性。
最后附上论文地址