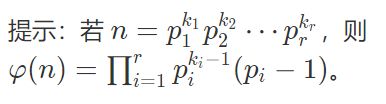计蒜客2019蓝桥杯省赛A组模拟赛(一)题目及解析
蓝桥杯历年真题题目及题解目录汇总
A. 结果填空:阶乘位数 题库链接
分值: 5
蒜头君对阶乘产生了兴趣,他列出了前 10 个正整数的阶乘以及对应位数的表:
| n | n! | 位数 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 1 |
| 3 | 6 | 1 |
| 4 | 24 | 2 |
| 5 | 120 | 3 |
| 6 | 720 | 3 |
| 7 | 5040 | 4 |
| 8 | 40320 | 5 |
| 9 | 362880 | 6 |
| 10 | 3628800 | 7 |
对于蒜头君来说,再往后就很难计算了。他试图寻找阶乘位数的规律,但是失败了。现在请你帮他计算出第一个正整数的阶乘位数大于等于 10000 的数是多少,即求最小的正整数 n 满足 n! 的位数大于等于 10000。
答案3249,细节,注意少点new对象,大数类的对象之类的,很耗时间,打牛客的时候入过坑
import java.math.BigInteger;
public class 阶乘位数 {
public static void main(String[] args) {
BigInteger n = BigInteger.valueOf(1);
BigInteger one =BigInteger.ONE;
BigInteger sum = BigInteger.ONE;
int len=0;
while(len<10000) {
n = n.add(one);
sum = sum.multiply(n);
len = sum.toString().length();
System.out.println(n+" "+len);
}
System.out.println("答案"+n);
}
}
B. 结果填空:炮台实验 题库链接
分值: 7
蒜头君在玩一个战争模拟游戏,他有高度为 1,2,3,…,n 的炮台各一个,他需要把这 n 个炮台从左往右排成一行,并且炮口都朝向右边。
在这个游戏中,所有炮台发射的炮弹会摧毁前方所有高度比自己低的炮台。每当蒜头君把 n 个炮台排成一行后,可能会有一些炮台被摧毁。举个例子:当前有 5 个炮台,从左到右高度分别为 2,1,3,5,4,往右发射炮弹后,高度为 4 的炮台被高度为 5 的摧毁,高度为 1 的炮台被高度为 2的炮台摧毁,最后只会剩下 2,3,5 这三个炮台。
现在蒜头君想知道,如果随机地摆放这 n 个炮台,最后剩下炮台个数的期望是多少?比如 n=2 时,有两种摆放方式,高度序列分别为 1,2 和 2,1,前者最后剩下 2 个炮台,后者最后剩下一个炮台,因此期望为(2+1)/2=1.5000。
请你求出 n=2019 时剩下炮台个数的期望,保留四位小数。
#include
using namespace std;
int main() {
double ans = 0;
int n = 2019;
for (int i = 1; i <= n; i++) {
ans += 1.0 / i;
}
printf("%.4f\n", ans);
return 0;
} C. 结果填空:马的管辖 题库链接
分值: 13
答案:90,和B组的一样。没看过B组的,建议先看
计蒜客2019蓝桥杯省赛B组模拟赛(一)题目及解析
D. 结果填空:修建公路 题库链接
分值: 17
蒜头国有 nn 座城市,编号分别为 0,1,2,3,…,n−1。编号为 xx 和 yy 的两座城市之间如果要修高速公路,必须花费 x∣y 个金币,其中|表示二进制按位或。
吝啬的国王想要花最少的价格修建高速公路,使得所有城市可以通过若干条高速公路互相达到。现在请你求出 n=2019 时,一共有多少不同的方案,能让所有城市连通并且造价最低。方案数可能很大,你只需输出对 10^9+7 取模的结果。
#include
#include
using namespace std;
typedef long long LL;
const LL mod = 1e9 + 7;
int main() {
int n = 2019;
LL ans = 1;
for (int i = 1; i < n; i++) {
int t = 0;
for (int j = 0; i >> j > 0; j++) {
if (i >> j & 1) t++;
}
ans = ans * ((1 << t) - 1) % mod;
}
printf("%lld\n", ans);
return 0;
} E. 代码填空:欧拉函数 题库链接
分值: 9
在数论中,对正整数 n,欧拉函数 ![]() 是小于等于 n 的正整数中与 n 互质的数的数目。
是小于等于 n 的正整数中与 n 互质的数的数目。
例如 ![]() = 4,因为 1,5,7,11 均和 12 互质。
= 4,因为 1,5,7,11 均和 12 互质。
代码框中的代码是一种求欧拉函数的实现,请分析并填写缺失的代码,计算出![]() 的值。
的值。
#include
using namespace std;
int euler(int n) {
int res = n;
for (int i = 2; i <= n; i++) {
if (n % i == 0) {
res = res - res / i;
while (n % i == 0) {
n /= i;
}
}
}
return res;
}
int main() {
int n;
cin >> n;
cout << euler(n) << endl;
return 0;
} F. 程序设计:掎角之势 题库链接
分值: 11
#include
#include
using namespace std;
int main() {
int T;
scanf("%d", &T);
while (T--) {
int x1, y1, x2, y2, x3, y3;
scanf("%d %d %d %d %d %d", &x1, &y1, &x2, &y2, &x3, &y3);
x1 -= x3;
y1 -= y3;
x2 -= x3;
y2 -= y3;
if (x1 * y2 == x2 * y1) {
puts("NO SOLUTION");
continue;
}
double s = fabs(x1 * y2 - x2 * y1);
double a = sqrt(x1 * x1 + y1 * y1);
double b = sqrt(x2 * x2 + y2 * y2);
double c = sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
double r1 = s / (a + b + c);
double r2 = a * b * c / s / 2;
printf("%.10f %.10f\n", r1 * r1 * acos(-1), r2 * r2 * acos(-1));
}
return 0;
} 暴力40%
#include
#include
using namespace std;
int main() {
int T;
scanf("%d", &T);
while (T--) {
int x1, y1, x2, y2, x3, y3;
scanf("%d %d %d %d %d %d", &x1, &y1, &x2, &y2, &x3, &y3);
if (y1 == 0 || x2 == 0) {
puts("NO SOLUTION");
continue;
}
double s = y1 * x2;
double c = sqrt(y1 * y1 + x2 * x2);
double r1 = s / (y1 + x2 + c);
double r2 = c / 2;
printf("%.10f %.10f\n", r1 * r1 * acos(-1), r2 * r2 * acos(-1));
}
return 0;
}
G. 程序设计:轻重搭配 题库链接
分值: 19
答案:这题也和B组的一样。没看过B组的,建议先看
计蒜客2019蓝桥杯省赛B组模拟赛(一)题目及解析
H. 程序设计:忽明忽暗 题库链接
分值: 21
#include
#include
#include
using namespace std;
int main() {
long long n, mod = 1e9 + 7;
cin >> n;
long long t = sqrt(n);
long long ans = t * (t + 1) / 2;
if (ans % 3 == 0) {
ans = ans / 3 % mod * (2 * t + 1) % mod;
} else {
ans = ans % mod * ((2 * t + 1) / 3) % mod;
}
cout << ans << endl;
return 0;
} #include
#include
#include
using namespace std;
int main() {
long long n, mod = 1e9 + 7;
cin >> n;
__int128 t = sqrt(n);
long long ans = t * (t + 1) * (2 * t + 1) / 6 % mod;
cout << ans << endl;
return 0;
} #include
#include
#include
using namespace std;
bool a[1000005];
int main() {
long long n, mod = 1e9 + 7;
cin >> n;
long long ans = 0;
for (int i = 1; i <= n; i++) {
for (int j = i; j <= n; j += i) {
a[j] = !a[j];
}
}
for (int i = 1; i <= n; i++) {
if (a[i]) ans += i;
}
cout << ans % mod << endl;
return 0;
} #include
#include
#include
using namespace std;
int main() {
long long n, mod = 1e9 + 7;
cin >> n;
long long t = sqrt(n);
long long ans = 0;
for (long long i = 1; i * i <= n; i++) {
ans += i * i;
ans %= mod;
}
cout << ans << endl;
return 0;
}
I. 程序设计:人以群分 题库链接
分值: 23
#include
#include
using namespace std;
const int N = 500005;
int n, m;
int a[N], dp[N];
bool check(int x) {
// dp[0~m-1]=0
for (int i = m; i <= n; i++) {
if (a[i] - a[dp[i - m] + 1] <= x) {
dp[i] = i;
} else {
dp[i] = dp[i - 1];
}
}
return dp[n] == n;
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
sort(a + 1, a + n + 1);
int l = 0, r = 1e9;
while (l < r) {
int mid = (l + r) >> 1;
if (check(mid)) {
r = mid;
} else {
l = mid + 1;
}
}
printf("%d\n", l);
return 0;
} 暴力30%
#include
#include
using namespace std;
const int N = 500005;
int n, m;
int a[N];
int ans = 0;
void dfs(int u, int x, int t) {
if (u == n) {
if (u - x + 1 >= m) {
t = max(t, a[u] - a[x]);
ans = min(ans, t);
}
return;
}
if (u - x + 1 >= m) {
dfs(u + 1, u + 1, max(t, a[u] - a[x]));
}
dfs(u + 1, x, t);
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
sort(a + 1, a + n + 1);
ans = 1e9;
dfs(1, 1, 0);
printf("%d\n", ans);
return 0;
} 暴力60%
#include
#include
using namespace std;
const int N = 500005;
int n, m;
int a[N], dp[N];
bool check(int x) {
// dp[0~m-1]=0
for (int i = m; i <= n; i++) {
if (a[i] - a[dp[i - m] + 1] <= x) {
dp[i] = i;
} else {
dp[i] = dp[i - 1];
}
}
return dp[n] == n;
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
sort(a + 1, a + n + 1);
for (int i = 0;; i++) {
if (check(i)) {
printf("%d\n", i);
break;
}
}
return 0;
} J. 程序设计:势能之和 题库链接
分值: 25
#include
using namespace std;
typedef long long LL;
const LL mod = 1e9 + 7;
const int N = 1000005;
int a[N];
LL two[N];
LL b[N];
LL inv[1000005];
void inv_init(int n) {
inv[1] = 1;
for (int i = 2; i <= n; i++) {
inv[i] = (mod - mod / i) * inv[mod % i] % mod;
}
}
int main() {
const int wc = 1e6;
two[0] = 1;
for (int i = 1; i <= wc; i++) {
two[i] = two[i - 1] * 2 % mod;
}
inv_init(wc);
int n;
scanf("%d", &n);
LL all = 1;
for (int i = 0; i < n; i++) {
int x;
scanf("%d", &x);
a[x]++;
all = all * x % mod;
}
LL ans = 0;
for (int i = wc; i >= 1; i--) {
int sum = a[i];
b[i] = 0;
for (int j = i + i; j <= wc; j += i) {
b[i] -= b[j];
sum += a[j];
}
b[i] += two[sum] - 1;
b[i] = (b[i] % mod + mod) % mod;
ans += b[i] * all % mod * inv[i] % mod;
}
ans %= mod;
printf("%lld\n", ans);
return 0;
} 暴力30%
#include
#include
using namespace std;
typedef long long LL;
const LL mod = 1e9 + 7;
const int N = 200005;
LL a[N];
int main() {
int n;
scanf("%d", &n);
LL all = 1;
for (int i = 0; i < n; i++) {
scanf("%lld", &a[i]);
all = all * a[i];
}
for (int i = 0; i < n; i++) {
a[i] = all / a[i];
}
LL ans = 0;
for (int s = 1; s < 1 << n; s++) {
LL tmp = 1;
for (int i = 0; i < n; i++) {
if (s >> i & 1) {
tmp = tmp / __gcd(tmp, a[i]) * a[i];
}
}
ans = (ans + tmp) % mod;
}
printf("%lld\n", ans);
return 0;
} 暴力60%
#include
#include
using namespace std;
typedef long long LL;
const LL mod = 1e9 + 7;
const int N = 200005;
LL a[N];
LL pow_mod(LL x, LL p) {
LL res = 1;
while (p) {
if (p & 1) res = res * x % mod;
p >>= 1;
x = x * x % mod;
}
return res;
}
int main() {
int n;
scanf("%d", &n);
LL all = 1;
for (int i = 0; i < n; i++) {
scanf("%lld", &a[i]);
all = all * a[i] % mod;
}
LL ans = 0;
for (int s = 1; s < 1 << n; s++) {
LL tmp = 0;
for (int i = 0; i < n; i++) {
if (s >> i & 1) {
tmp = __gcd(a[i], tmp);
}
}
ans = (ans + all * pow_mod(tmp, mod - 2)) % mod;
}
printf("%lld\n", ans);
return 0;
}