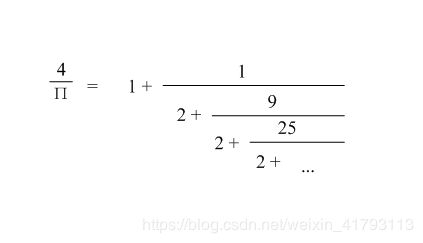2014年第五届蓝桥杯省赛试题及详解(Java本科B组)
蓝桥杯历年真题题目及题解目录汇总
- 结果填空 (满分2分)
- 结果填空 (满分5分)
- 结果填空 (满分6分)
- 代码填空 (满分4分)
- 代码填空 (满分9分)
- 结果填空 (满分11分)
- 结果填空 (满分15分)
- 程序设计(满分7分)
- 程序设计(满分18分)
- 程序设计(满分23分)
1.标题:武功秘籍
小明到X山洞探险,捡到一本有破损的武功秘籍(2000多页!当然是伪造的)。他注意到:书的第10页和第11页在同一张纸上,但第11页和第12页不在同一张纸上。
小明只想练习该书的第81页到第92页的武功,又不想带着整本书。请问他至少要撕下多少张纸带走?
这是个整数,请通过浏览器提交该数字,不要填写任何多余的内容。
7,(80,81),(82,83),(84,85),(86,87),(88,89),(90,91),(91,92)
题目告诉你2000多页,10-11连在一起,说明没过对称轴,就好数了,如果告诉你10和2000一页呢?
2.标题:切面条
一根高筋拉面,中间切一刀,可以得到2根面条。
如果先对折1次,中间切一刀,可以得到3根面条。
如果连续对折2次,中间切一刀,可以得到5根面条。
那么,连续对折10次,中间切一刀,会得到多少面条呢?
答案是个整数,请通过浏览器提交答案。不要填写任何多余的内容。
1025,脑补了一下,二分有关,猜下公式2^n+1,再推下n=3的情况,就差不多了
3.标题:猜字母
把abcd...s共19个字母组成的序列重复拼接106次,得到长度为2014的串。
接下来删除第1个字母(即开头的字母a),以及第3个,第5个等所有奇数位置的字母。
得到的新串再进行删除奇数位置字母的动作。如此下去,最后只剩下一个字母,请写出该字母。
答案是一个小写字母,请通过浏览器提交答案。不要填写任何多余的内容。
按照它说的做就好,不过我26个字母不会排,好在有ASCII码,答案:q
String会内存溢出,用StringBuilder,StringBuilder的好处就是修改多次有优势,百度下
public class 猜字母 {
public static void main(String[] args) {
//abcdefghijklmnopqrs
StringBuilder s = new StringBuilder("abcdefghijklmnopqrs");
for(int i=1;i<=105;i++)
s.append("abcdefghijklmnopqrs");
while(s.length()>1) {
System.out.println(s.length());
StringBuilder s1 = new StringBuilder();
for(int i=1;ireplace()函数
/*
题目:猜字母
把abcd...s共19个字母组成的序列重复拼接106次,得到长度为2014的串。
接下来删除第1个字母(即开头的字母a),以及第3个,第5个等所有奇数位置的字母。
得到的新串再进行删除奇数位置字母的动作。如此下去,最后只剩下一个字母,请写出该字母。
答案:q
*/
#include
using namespace std;
int main(){
string s="abcdefghijklmnopqrs";
string ss;
for(int i=0;i<106;i++){
ss+=s; //拼接106次
}
while(ss.size()>1){ //判断循环结束
for(int i=0;i
4.标题:大衍数列
中国古代文献中,曾记载过“大衍数列”, 主要用于解释中国传统文化中的太极衍生原理。
它的前几项是:0、2、4、8、12、18、24、32、40、50 ...
其规律是:对偶数项,是序号平方再除2,奇数项,是序号平方减1再除2。
以下的代码打印出了大衍数列的前 100 项。
for(int i=1; i<100; i++)
{
if(________________) //填空
System.out.println(i*i/2);
else
System.out.println((i*i-1)/2);
}请填写划线部分缺失的代码。通过浏览器提交答案。
注意:不要填写题面已有的内容,也不要填写任何说明、解释文字。
i%2==0
5.标题:圆周率
数学发展历史上,圆周率的计算曾有许多有趣甚至是传奇的故事。其中许多方法都涉及无穷级数。
图1.png中所示,就是一种用连分数的形式表示的圆周率求法。
下面的程序实现了该求解方法。实际上数列的收敛对x的初始值 并不敏感。
结果打印出圆周率近似值(保留小数点后4位,并不一定与圆周率真值吻合)。
double x = 111;
for(int n = 10000; n>=0; n--){
int i = 2 * n + 1;
x = 2 + (i*i / x);
}
System.out.println(String.format("%.4f", ______________));
4.0/(x-1)
6.标题:奇怪的分式
上小学的时候,小明经常自己发明新算法。一次,老师出的题目是:
1/4 乘以 8/5
小明居然把分子拼接在一起,分母拼接在一起,答案是:18/45 (参见图1.png)
老师刚想批评他,转念一想,这个答案凑巧也对啊,真是见鬼!
对于分子、分母都是 1~9 中的一位数的情况,还有哪些算式可以这样计算呢?
请写出所有不同算式的个数(包括题中举例的)。
显然,交换分子分母后,例如:4/1 乘以 5/8 是满足要求的,这算做不同的算式。
但对于分子分母相同的情况,2/2 乘以 3/3 这样的类型太多了,不在计数之列!
注意:答案是个整数(考虑对称性,肯定是偶数)。请通过浏览器提交。不要书写多余的内容。
14,暴力4个for 打印验证
public class _06奇怪的分式 {
public static void main(String[] args) {
// A/B x C/D = E/F A*C*F = E*B*D
int ans=0;
for(int a=1;a<10;a++)
for(int b=1;b<10;b++)
for(int c=1;c<10;c++)
for(int d=1;d<10;d++) {
int e = 10*a+c;
int f = 10*b+d;
if(a==b || c==d)
continue;
if(a*c*f==e*b*d) {
ans++;
System.out.println(a+"/"+b+" x "+c+"/"+d+" = "+e+"/"+f+" "+ans);
}
}
}
}
7.标题:扑克序列
A A 2 2 3 3 4 4, 一共4对扑克牌。请你把它们排成一行。
要求:两个A中间有1张牌,两个2之间有2张牌,两个3之间有3张牌,两个4之间有4张牌。
请填写出所有符合要求的排列中,字典序最小的那个。
例如:22AA3344 比 A2A23344 字典序小。当然,它们都不是满足要求的答案。
请通过浏览器提交答案。“A”一定不要用小写字母a,也不要用“1”代替。字符间一定不要留空格。
2342A3A4,又是一道全排,因为A是比2大的那么把A看成5就好
public class _07扑克序列1 {
public static void main(String[] args) {
dfs(0);
}
static int[] a = new int[] {5,5,2,2,3,3,4,4};
static void dfs(int m) {
if(m>=8) {
int A1=-1,A2=-1,B1=-1,B2=-1,C1=-1,C2=-1,D1=-1,D2=-1;
for(int i=0;i<8;i++)
if(a[i]==5) {
if(A1==-1)
A1 = i;
else
A2 = i;
}else if(a[i]==2) {
if(B1==-1)
B1 = i;
else
B2 = i;
}else if(a[i]==3) {
if(C1==-1)
C1 = i;
else
C2 = i;
}else if(a[i]==4) {
if(D1==-1)
D1 = i;
else
D2 = i;
}
if(A2-A1!=2 || B2-A1!=3 || C2-C1!=4 || D2-D1!=5)
return;
for(int i=0;i<8;i++)
if(a[i]==5)
System.out.print("A");
else
System.out.print(a[i]);
System.out.println();
return;
}
for(int i=m;i<8;i++) {
swap(i,m);
dfs(m+1);
swap(i,m);
}
}
static void swap(int i,int j) {
int t = a[i];
a[i] = a[j];
a[j] = t;
}
}8.标题:分糖果
有n个小朋友围坐成一圈。老师给每个小朋友随机发偶数个糖果,然后进行下面的游戏:
每个小朋友都把自己的糖果分一半给左手边的孩子。
一轮分糖后,拥有奇数颗糖的孩子由老师补给1个糖果,从而变成偶数。
反复进行这个游戏,直到所有小朋友的糖果数都相同为止。
你的任务是预测在已知的初始糖果情形下,老师一共需要补发多少个糖果。
【格式要求】
程序首先读入一个整数N(2
要求程序输出一个整数,表示老师需要补发的糖果数。
例如:输入
3
2 2 4
程序应该输出:
4
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
模拟,模拟每一轮操作
import java.util.Scanner;
public class _08分糖果 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] a = new int[n];
int[] b = new int[n];
int ans=0;
for(int i=0;i
9.标题:地宫取宝
X 国王有一个地宫宝库。是 n x m 个格子的矩阵。每个格子放一件宝贝。每个宝贝贴着价值标签。
地宫的入口在左上角,出口在右下角。
小明被带到地宫的入口,国王要求他只能向右或向下行走。
走过某个格子时,如果那个格子中的宝贝价值比小明手中任意宝贝价值都大,小明就可以拿起它(当然,也可以不拿)。
当小明走到出口时,如果他手中的宝贝恰好是k件,则这些宝贝就可以送给小明。
请你帮小明算一算,在给定的局面下,他有多少种不同的行动方案能获得这k件宝贝。
【数据格式】
输入一行3个整数,用空格分开:n m k (1<=n,m<=50, 1<=k<=12)
接下来有 n 行数据,每行有 m 个整数 Ci (0<=Ci<=12)代表这个格子上的宝物的价值
要求输出一个整数,表示正好取k个宝贝的行动方案数。该数字可能很大,输出它对 1000000007 取模的结果。
例如,输入:
2 2 2
1 2
2 1
程序应该输出:
2
再例如,输入:
2 3 2
1 2 3
2 1 5
程序应该输出:
14
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
问题 1436: [蓝桥杯][2014年第五届真题]地宫取宝
之前写过,不过隔的久,风格有点差别,记忆化搜索,这里是从出口到入口的递归,那个博客是入口开始的,初始化为-1的话,判断完后记得设为0,不然你的答案莫名的-1-1-1,用四维数组记忆
import java.util.Scanner;
public class _09地宫取宝1 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
n = in.nextInt();
m = in.nextInt();
k = in.nextInt();
a = new int[n+5][m+5];
int max=0;
for(int i=0;ia[x][y])
return 1;
return 0;
}
memo[x][y][now][max] = 0;
if(now>0) {
if(x>0) {
memo[x][y][now][max] = (memo[x][y][now][max]+f(x-1,y,now,max))%1000000007;
if(max>a[x][y])
memo[x][y][now][max] = (memo[x][y][now][max]+f(x-1,y,now-1,a[x][y]))%1000000007;
}
if(y>0) {
memo[x][y][now][max] = (memo[x][y][now][max]+f(x,y-1,now,max))%1000000007;
if(max>a[x][y])
memo[x][y][now][max] = (memo[x][y][now][max]+f(x,y-1,now-1,a[x][y]))%1000000007;
}
} else {
if(x>0)
memo[x][y][now][max] = (memo[x][y][now][max]+f(x-1,y,now,max))%1000000007;
if(y>0)
memo[x][y][now][max] = (memo[x][y][now][max]+f(x,y-1,now,max))%1000000007;
}
return memo[x][y][now][max]%1000000007;
}
}
10.标题:矩阵翻硬币
小明先把硬币摆成了一个 n 行 m 列的矩阵。
随后,小明对每一个硬币分别进行一次 Q 操作。
对第x行第y列的硬币进行 Q 操作的定义:将所有第 i*x 行,第 j*y 列的硬币进行翻转。
其中i和j为任意使操作可行的正整数,行号和列号都是从1开始。
当小明对所有硬币都进行了一次 Q 操作后,他发现了一个奇迹——所有硬币均为正面朝上。
小明想知道最开始有多少枚硬币是反面朝上的。于是,他向他的好朋友小M寻求帮助。
聪明的小M告诉小明,只需要对所有硬币再进行一次Q操作,即可恢复到最开始的状态。然而小明很懒,不愿意照做。于是小明希望你给出他更好的方法。帮他计算出答案。
【数据格式】
输入数据包含一行,两个正整数 n m,含义见题目描述。
输出一个正整数,表示最开始有多少枚硬币是反面朝上的。
【样例输入】
2 3
【样例输出】
1
【数据规模】
对于10%的数据,n、m <= 10^3;
对于20%的数据,n、m <= 10^7;
对于40%的数据,n、m <= 10^15;
对于10%的数据,n、m <= 10^1000(10的1000次方)。
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
数学题,考点太多了
- 第x行第y列被翻动的总次数?
- 考虑第1行,第y列,y有多少真因子,就会被翻动多少次,而所有的y中,只有平方数的真因子个数为奇数(约数总是成对出现的)
- 考虑第1列,第x行,x有多少真因子,就会被翻动多少次,而所有的x中,只有平方数的真因子个数为奇数
- x,y硬币被翻动的次数=x真因子个数*y真因子个数,只有奇数*奇数=奇数,所以,若要x,y为反面,必须x,y都是平方数
- 因此,反面硬币总数=m中的平方数的个数*n中平方数的个数
- 那么在m中有多少个平方数呢?答案是sqrt(m)向下取整个,如9内有三个平方数1,4,9;16里面有4个平方数1,4,9,16;25内有5个平方数
- 因此此题等价于求sqrt(m)*sqrt(n),那么怎么对一个很大的数开平方呢?
- 假设一个数的长度为length,其平方根的长度为length/2(偶数)或者length/2+1(奇数)
- 我们可以从高位不停地试探,每一个取平方后恰好不超过目标平方数的值
/*
标题:矩阵翻硬币
小明先把硬币摆成了一个 n 行 m 列的矩阵。
随后,小明对每一个硬币分别进行一次 Q 操作。
对第x行第y列的硬币进行 Q 操作的定义:将所有第 i*x 行,第 j*y 列的硬币进行翻转。
其中i和j为任意使操作可行的正整数,行号和列号都是从1开始。
当小明对所有硬币都进行了一次 Q 操作后,他发现了一个奇迹——所有硬币均为正面朝上。
小明想知道最开始有多少枚硬币是反面朝上的。于是,他向他的好朋友小M寻求帮助。
聪明的小M告诉小明,只需要对所有硬币再进行一次Q操作,即可恢复到最开始的状态。然而小明很懒,不愿意照做。于是小明希望你给出他更好的方法。帮他计算出答案。
【数据格式】
输入数据包含一行,两个正整数 n m,含义见题目描述。
输出一个正整数,表示最开始有多少枚硬币是反面朝上的。
【样例输入】
2 3
【样例输出】
1
【数据规模】
对于10%的数据,n、m <= 10^3;
对于20%的数据,n、m <= 10^7;
对于40%的数据,n、m <= 10^15;
对于100%的数据,n、m <= 10^1000(10的1000次方)。
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
*/
import java.math.BigInteger;
import java.util.Arrays;
import java.util.Scanner;
//第x行第y列被翻动的总次数?
//考虑第1行,第y列,y有多少真因子,就会被翻动多少次,而所有的y中,只有平方数的真因子个数为奇数(约数总是成对出现的)
//考虑第1列,第x行,x有多少真因子,就会被翻动多少次,而所有的x中,只有平方数的真因子个数为奇数
//x,y硬币被翻动的次数=x真因子个数*y真因子个数,只有奇数*奇数=奇数,所以,若要x,y为反面,必须x,y都是平方数
//因此,反面硬币总数=m中的平方数的个数*n中平方数的个数
//那么在m中有多少个平方数呢?答案是sqrt(m)向下取整个,如9内有三个平方数1,4,9;16里面有4个平方数1,4,9,16;25内有5个平方数
//因此此题等价于求sqrt(m)*sqrt(n),那么怎么对一个很大的数开平方呢?
//假设一个数的长度为length,其平方根的长度为length/2(偶数)或者length/2+1(奇数)
//我们可以从高位不停地试探,每一个取平方后恰好不超过目标平方数的值
public class _10矩阵翻硬币 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String s1 = sc.next();
String s2 = sc.next();
System.out.println(sqrt(s1).multiply(sqrt(s2)));
}
private static BigInteger sqrt(String s) {
int length = s.length();
int len = 0;
if (length % 2 == 0)
len = length / 2;
else
len = length / 2 + 1;
char[] sArr = new char[len];
Arrays.fill(sArr, '0');
BigInteger target = new BigInteger(s);
for (int pos = 0; pos < len; pos++) {
for (char c = '1'; c <= '9'; c++) {
sArr[pos] = c;//在pos这个位置上试着填入1-9
BigInteger pow = new BigInteger(String.valueOf(sArr)).pow(2);//平方
if (pow.compareTo(target) == 1)//试探数的平方更大
{
sArr[pos] -= 1;
break;
}
}
}
return new BigInteger(String.valueOf(sArr));
}
}
小结:
01 武功秘籍 书的构造方式,思维题 02 切面条 发现规律,思维题 03 猜字母 数组中元素的挪动和挤压 04 大衍数列 考察奇偶数判断 05 圆周率 细心,极限思维 06 奇怪的分式 枚举abcd,分数运算,最大公约数 07 扑克排序 带重复元素的全排列 08 分糖果 模拟 **09 地宫取宝 搜索->记忆型递归,因为子问题重复求解 ****10 矩阵翻硬币 数学;字符,字符串,BigInteger的互相转化