吴恩达深度学习第一课第三周作业及学习心得体会
概述
在完成吴恩达第一课第三周,即1hiddenlayer的neuralnetwork学习后,了解了两层神经网络的结构,然后参考网上的资料,完成该周作业,现将心得体会记录如下。
核心代码
- 调用库如下所示;
import numpy as np
import matplotlib.pyplot as plt- Sigmoid函数;
def sigmoid(z):
return 1.0/(1+np.exp(-z))- 初始化参数函数;
def initialize_parameters(n_x,n_h,n_y):
np.random.seed(2)
W1=np.random.randn(n_h,n_x)*0.01
b1=np.zeros((n_h,1))
W2=np.random.randn(n_y,n_h)*0.01
b2=np.zeros((n_y,1))
parameters={'W1':W1,
'b1':b1,
'W2':W2,
'b2':b2}
return parameters- 前向传播函数;
def forward_propagation(X,parameters):
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
Z1=np.dot(W1,X)+b1
A1=np.tanh(Z1)
Z2=np.dot(W2,A1)+b2
A2=sigmoid(Z2)
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return A2, cache- 成本函数;
def compute_cost(A2,Y):
m=Y.shape[1]
cost=-1.0/m*np.sum(np.multiply(Y,np.log(A2))+np.multiply((1-Y),np.log(1-A2)))
cost=np.squeeze(cost) # makes sure cost is the dimension we expect.
assert(isinstance(cost,float))
return cost- 反向传播函数;
def backward_propagation(parameters,cache,X,Y):
m = X.shape[1]
W2=parameters['W2'] #n_y,n_h
A1=cache['A1'] #n_h,m
A2=cache['A2'] #n_y,m
dZ2=A2-Y #n_y,m
dW2=1.0/m*np.dot(dZ2,A1.T) #n_y,n_h
db2=1.0/m*np.sum(dZ2,axis=1,keepdims=True) #n_y,1
dZ1=np.multiply(np.dot(W2.T,dZ2),(1-A1**2)) #n_h,m
dW1=1.0/m*np.dot(dZ1,X.T) #n_h,n_x
db1=1.0/m*np.sum(dZ1,axis=1,keepdims=True) #n_h,1
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2}
return grads- 参数更新函数;
def update_parameters(parameters,grads,learning_rate):
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
dW1 = grads["dW1"]
db1 = grads["db1"]
dW2 = grads["dW2"]
db2 = grads["db2"]
###梯度更新,每迭代一次更新一次###
W1 -= learning_rate * dW1
b1 -= learning_rate * db1
W2 -= learning_rate * dW2
b2 -= learning_rate * db2
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters- 构建模型函数;
def nn_model(X,Y,n_h,num_iterations,learning_rate,print_cost):
np.random.seed(3)
n_x=X.shape[0]
n_y=Y.shape[0]
parameters=initialize_parameters(n_x,n_h,n_y)
for i in range(0,num_iterations):
A2,cache=forward_propagation(X,parameters)#前向传播节点
cost = compute_cost(A2, Y)#计算损失函数
grads=backward_propagation(parameters,cache,X,Y)#计算后向传播梯度
parameters=update_parameters(parameters,grads,learning_rate)#使用梯度更新W,b一次
if print_cost and i % 1000 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
return parameters- 预测函数。
def predict(X,parameters):
A2, cache = forward_propagation(X, parameters)
predictions = (A2 > 0.5)
return predictions二元分类问题
二元分类问题1
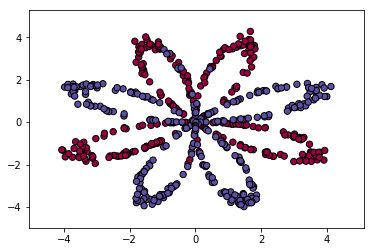
训练数据为二维平面的坐标点,形状呈8瓣花瓣,其中设置部分点标签为0,另一部分为1,代码如下:
#产生数据
np.random.seed(1)
m = 600 #样本数
N = int(m/2) #分为两类
D = 2 #样本的特征数或维度
X = np.zeros((m,D)) #初始化样本坐标
Y = np.zeros((m,1)) #初始化样本标签
a = 4 #基础半径
for j in range(2):
ix = range(N*j,N*(j+1))#ix=(0,199)(200,399)
t = np.linspace(j*3.12,(j+1)*3.12,N) + np.random.randn(N)*0.2 #theta角度,产生200个角度并加入随机数,保证角度随机分开,图像开起来稀疏程度不一
r = a*np.sin(4*t) + np.random.randn(N)*0.2 #radius半径,4sin(4*t),并加入一定的随机,图像轨道不平滑
X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] #生成坐标点
Y[ix] = j #red or blue数据绘出如下图图所示。
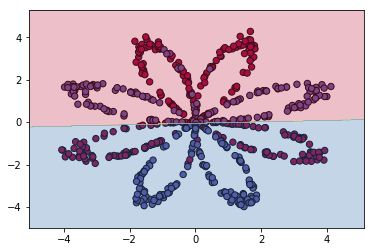
先对这些点通过逻辑回归进行训练,对样本重新预测的准确率为0.468333。可见逻辑回归处理这类交叉分布的问题,效果一般,对二维平面进行预测并分区,结果如下图所示(分区的步骤是,先将二维平面分成0.01*0.01的小块,用numpy库的meshgrid函数可实现该功能;然后每个块对应一个坐标;再使用逻辑回归对这些坐标数据进行预测,得到每个坐标的标签0或1;最后使用matplotlib.pyplot库的contourf函数进行分区,该函数用于绘制等高线。这一部分功能请读者自行完成)。
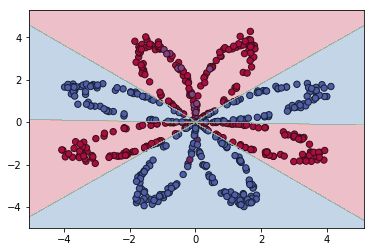
然后再用这些点训练1hiddenlayer的neuralnetwork(神经元个数为4),得到其参数,用其对样本重新预测准确率为0.941667,二维平面预测并分区,结果如下图所示:
二元分类问题2
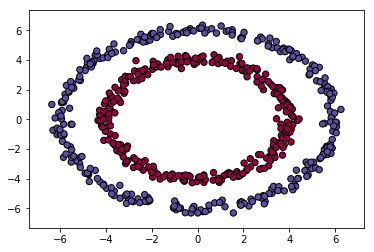
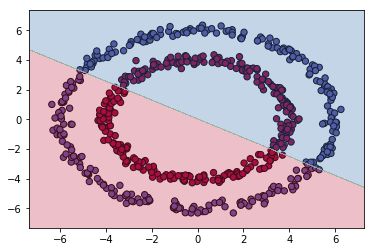
将训练的坐标点更改为两组环形圈,两层标签分别为0和1,代码如下
np.random.seed(1)
m = 600 #样本数
N = int(m/2) #分为两类
D = 2 #样本的特征数或维度
X = np.zeros((m,D)) #初始化样本坐标
Y = np.zeros((m,1)) #初始化样本标签
a = 4 #基础半径
for j in range(2):
ix = range(N*j,N*(j+1))#ix=(0,199)(200,399)
t = np.linspace(0,6.28,N) + np.random.randn(N)*0.1 #theta角度,产生200个角度并加入随机数,保证角度随机分开,图像开起来稀疏程度不一
r = (a + j*2) + np.random.randn(N)*0.2 #radius半径,4sin(4*t),并加入一定的随机,图像轨道不平滑
X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] #生成坐标点
Y[ix] = j #red or blue点绘出后如下图所示。
先对这些点通过逻辑回归进行训练,训练后对样本重新预测的准确率为0.468333,效果一般。对二维平面预测并分区,结果如下图所示。
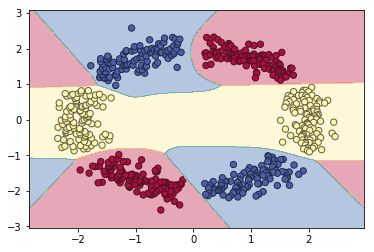
然后再用这些点训练1hiddenlayer的neuralnetwork(神经元个数为5),得到其参数,用其对样本重新预测准确率为1,二维平面预测并分区,结果如下图所示(调试时发现隐藏单元的神经元个数过多时,容易产生过拟合)。
三元分类问题
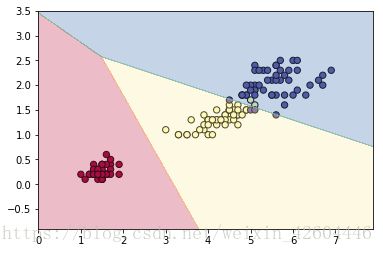
在第二周的学习中,注意到sklearn库中的逻辑回归是可以处理iris这种三元分类的问题的。Iris的数据有4列,取第3列(下标为2)为横坐标,第4列(下标为3)为纵坐标时,三类数据基本不交叉,通过sklearn库中的逻辑回归训练,对样本预测,准确率为0.953333,对二维平面预测并分区,结果如下图所示。
在进行第三周的学习时,考虑这类NN能否解决三元分类的问题。经设计调试,找到了几种解决方法。
Iris三元分类问题解决方法1
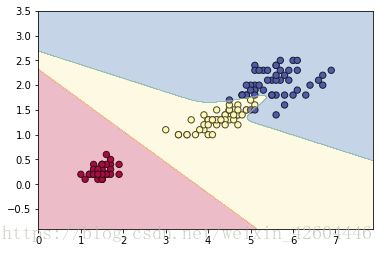
因为要处理三元分类问题,其标签为0 1 2,因此进行了两次分类。
- 第一次分类时,将1 2归为一类,令这两组数据的标签等于1,然后通过神经网络进行一次二元分类。
- 第二次分类有两种方法:
- 一种是将上一次分类标签为1的数据在按照原始标签1 2再进行分类,这种方法的预测率也很不错,但是在进行二维平面预测分区时,因为对数组的处理太麻烦,容易出错,最终未使用这种方法;
- 第二种方法,再对全部数据进行一次二元分类,但令标签为0 1的两组数据标签为0,标签为2数据标签为1。
第二次分类,使用第二种方法,经过两次训练和预测后,将两次预测结果直接相加即可!
0 0 1
+
0 1 1
=
0 1 2
因前面的二层神经网络算法部分代码一致,因此仅贴最后的分类代码如下,其中对预测结果要+0,否则其内容均为False或True,相加后仍为False或True,+0后变为0或1,相加后和等于0或1或2。数组zz即整个二维平面坐标数组。
#第1次分类
m = len(y)
X_0 = X #以X为样本,赋给X_0
Y_0 = (y!=0) #y的标签本来等于0 1 2,先将1 2归为1类,令其标签=1
Y_0 = Y_0.reshape(1,m)
parameters = nn_model(X_0, Y_0, n_h=3, num_iterations=30000, learning_rate=2.2, print_cost=False) #以X_0为样本训练神经网络
y_0_NN_predict = predict(X_0,parameters) + 0 #根据训练出来的神经网络,对X进行预测
zz_0 = zz.T
Z_0 = predict(zz_0,parameters) + 0 #通过神经网络对二维图每个点进行第一次预测
#第2次分类
m = len(y)
X_1 = X #以X为样本,赋给X_1
Y_1 = (y==2) #y的标签本来等于0 1 2,再将0 1归为1类,令其标签=0
Y_1 = Y_1.reshape(1,m)
parameters = nn_model(X_1, Y_1, n_h=5, num_iterations=30000, learning_rate=0.5, print_cost=False) #以X_1为样本训练神经网络
y_1_NN_predict = predict(X_1,parameters) + 0 #根据训练出来的神经网络,对X进行预测
zz_1 = zz.T
Z_1 = predict(zz_1,parameters) + 0 #通过神经网络对二维图每个点进行第二次预测训练后,对样本预测,正确率达到0.986667,对二维平面预测并分区,运行结果如下图所示。
Iris三元分类问题解决方法2
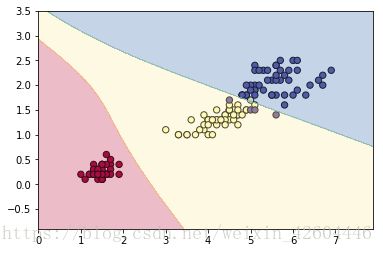
代码文件neuralnetwork_1hiddenlayer_iris_2_ReLU.Py。因为处理的是三元分类,而问题的根源在于sigmoid函数输出只能是0~1,因此考采用ReLU函数作为最终的激活函数。
需要更改的部分如下:
- 输出的激活函数改为ReLU函数;
def ReLU(z):
return (z+abs(z))/2- 前向传播过程;
def forward_propagation(X,parameters):
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
Z1=np.dot(W1,X)+b1
A1=np.tanh(Z1)
Z2=np.dot(W2,A1)+b2
A2=ReLU(Z2)
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return A2, cache- 更改成本函数,显然不能再用yloga+(1-y)log(1-a)了,因为y=0,1,2,a的范围是0~2。考虑到前面学到的也就(a-y)2/2这个函数了,也比较合适;
def compute_cost(A2,Y):
m=Y.shape[1]
cost=1.0/2.0/m*np.sum(np.multiply((A2-Y),(A2-Y)))
return cost- 反向传播过程,成本函数(a-y)2/2的导数正好是a-y,考虑到ReLU的导数在a>0时为1,a<0为0。因此在该例程中,反向传播时,当A2>0,正好dZ2=A2-Y(与逻辑回归一致!),当A2<0时,dZ2=0。
def backward_propagation(parameters,cache,X,Y):
m = X.shape[1]
W2=parameters['W2'] #n_y,n_h
A1=cache['A1'] #n_h,m
A2=cache['A2'] #n_y,m
dZ2=A2-Y
dZ2[:,A2[0,:]<0]=0
dW2=1.0/m*np.dot(dZ2,A1.T) #n_y,n_h
db2=1.0/m*np.sum(dZ2,axis=1,keepdims=True) #n_y,1
dZ1=np.multiply(np.dot(W2.T,dZ2),(1-A1**2)) #n_h,m
dW1=1.0/m*np.dot(dZ1,X.T) #n_h,n_x
db1=1.0/m*np.sum(dZ1,axis=1,keepdims=True) #n_h,1
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2}
return grads- 预测函数,因为预测结果应该是0 1 2。
def predict(X,parameters):
A2, cache = forward_propagation(X, parameters)
predictions = np.zeros(A2.shape[1])+1
predictions[A2[0,:]<0.5] = 0
predictions[A2[0,:]>1.5] = 2
return predictions,A2最终样本预测准确率为0.96,二维平面预测分区结果如下图所示。
交叉三元分类问题解决方案
对于有交叉的三元分类问题,上面方案1是肯定不可行的。因此考虑不更改输出的激活函数和成本函数,而是将输出由1个数值0或1或2,改为一个向量 [1,0,0]或[0,1,0]或[0,0,1]。
主要更改部分如下:
- 更改输入数据;
np.random.seed(1)
m = 600 #样本数
N = int(m/2) #分为两类
D = 2 #样本的特征数或维度
X = np.zeros((m,D)) #初始化样本坐标
y = np.zeros((m,1)) #初始化样本标签
Y = np.zeros((m,3)) #初始化样本标签
a = 2 #基础半径
for j in range(6):
ix = range((m//6)*j, (m//6)*(j+1))
t = np.linspace((3.14/3)*j+0.1, (3.14/3)*(j+1)-0.1, m//6) #theta角度,产生200个角度并加入随机数,保证角度随机分开,图像开起来稀疏程度不一
r = a + np.random.randn(m//6)*0.2 #radius半径,4sin(4*t),并加入一定的随机,图像轨道不平滑
X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] #生成坐标点
y[ix] = j%3
if j%3==0:
Y[ix] = [1,0,0]
if j%3==1:
Y[ix] = [0,1,0]
if j%3==2:
Y[ix] = [0,0,1]- 预测函数,因为预测结果应该是3×m的矩阵。
def predict(X,parameters):
A2, cache = forward_propagation(X, parameters)
predictions = np.zeros(A2.T.shape)
for i in range(A2.shape[1]):
if np.max(A2[:,i])==A2[0,i]:
predictions[i] = [1,0,0]
if np.max(A2[:,i])==A2[1,i]:
predictions[i] = [0,1,0]
if np.max(A2[:,i])==A2[2,i]:
predictions[i] = [0,0,1]
return predictions.T
该训练集绘出后如下图所示。
用sklearn库的逻辑回归进行训练,对样本重新预测的准确率为0.36,二维平面分区结果如下。
再用1hiddenlayer的NN进行训练,对样本进行预测,准确率达到1,对二维平面预测并分区,结果如下图所示,可见发生了过度预测。
-
猫识别问题
数据文件,在datasets文件夹内,分别包括训练数据和测试数据;
自己的图片文件,在images内,用于检验网络;
代码文件,CatRecognition_NN_1hiddenlayer.py(将上面核心代码敲入)。
代码文件中前面主要是读取文件代码,其中样本文件有209个,读取后的数据维度为209×64×64×3,其中209为样本数,两个64分别为图片的横纵像素个数,最后的3对应每个像素的RGB值。读取后将其转换为12288×209的二维矩阵,其中12288=64×64×3,即每个样本有12288个特征。
将1hiddenlayerNN的核心代码敲入,并用训练数据集进行训练,然后对训练数据和测试数据分别进行预测,准确率分别为0.990431和0.76,相较于第一课第二周作业中的逻辑回归而言有所提高(逻辑回归为1和0.7),过拟合程度降低。
对"images/cat7.jpg"(如下图所示)进行预测来检验网络。网络认为其不是猫,该网络准确率比较一般。注意预测时要将其resize为64×64。
总结
通过学习和实践,掌握了1hiddenlayerNN的设计方法,并且思考用所学的简单知识,尝试解决三元分类问题,最终正确实现,为后面的深层NN学习奠定基础。
附
想要源代码的同学,可以在我csdn账号下的资源里找,名字叫“吴恩达第一课第三周学习心得体会”,压缩包里面也有这边博客的word和pdf版本,祝学习愉快!