冒泡排序VS直接插入排序
冒泡排序VS直接插入排序
我们先思考一个问题:如何衡量一个排序算法的优劣呢?
一般来讲我们可从三个方面来看:
1.算法的时间效率:
a.时间复杂度:最好、最坏、平均时间复杂度相结合判断。
b.时间复杂度系数、低阶、常数的影响(因只有元素数量足够多时才可忽略系数、低阶、常数的影响,否则不可忽略)。
c.比较交换次数。
2.算法的内存消耗:
通过空间复杂度衡量。
3.算法的稳定性(重要)
算法的稳定性是指若在待排序的集合中存在数值相等的元素,判断集合有序后数值相等元素相对位置是否改变,若未改变,则为稳定性排序。
算法稳定性图解:
另外介绍一下原地排序的概念:原地排序是特指空间复杂度为O(1)的排序算法。
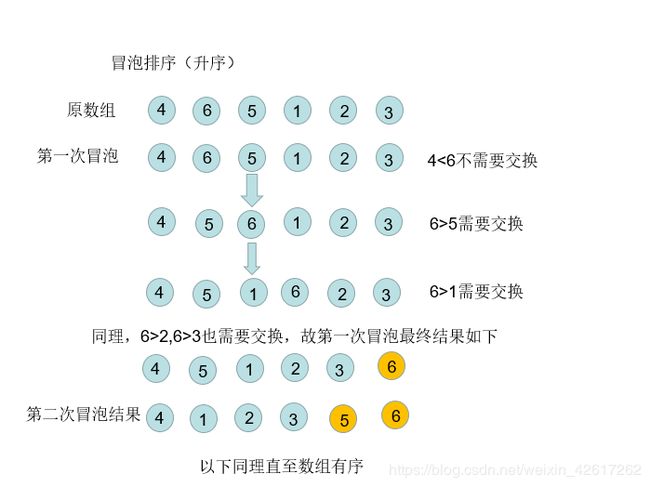
冒泡排序
冒泡排序每次只会操作相邻两个元素,对其做大小比较,看是否满足于题目要求排序。每次都会保证有一个元素被移动到最终位置。
冒泡排序图解:
public class Test {
public static void main(String[] args) {
int[] data=new int[]{6,4,5,1,2,3};
bubbleSort(data);
for(int i:data){
System.out.print(i+" ");
}
}
public static void bubbleSort(int[] data){
int n=data.length;
if(n<=1){//判断若数组为空或只有一个元素时直接返回即可
return;
}
for(int i=0;i<n;i++){//控制循环次数
for(int j=0;j<n-i-1;j++){//控制下次遍历元素个数(因已移动到最终位置的元素不需要遍历)
if(data[j]>data[j+1]){
data[j]^=data[j+1];
data[j+1]^=data[j];
data[j]^=data[j+1];
}
}
}
}
}
因数组元素可能在冒泡几次后已经有序,故可提前退出。所以冒泡排序可进行优化,优化思路为设立一个标志点进行判断(若某次元素间无交换就说明数组已经有序)
优化代码如下:
public class Test {
public static void main(String[] args) {
int[] data=new int[]{6,4,5,1,2,3};
bubbleSort(data);
for(int i:data){
System.out.print(i+" ");
}
}
public static void bubbleSort(int[] data){
int n=data.length;
if(n<=1){
return;
}
for(int i=0;i<n;i++){
boolean flag=false;//设立标志点默认为false
for(int j=0;j<n-i-1;j++){
if(data[j]>data[j+1]){
flag=true;//若有元素交换则标志点为true
data[j]^=data[j+1];
data[j+1]^=data[j];
data[j]^=data[j+1];
}
}
if(!flag){//判断标志点,若标志点为false即可认为数组有序,直接跳出即可
System.out.println("冒泡"+i+"次后数组有序");
break;
}
}
}
}
我们通过代码可以看出冒泡排序最好排序时间复杂度为O(n)(情况为数组正好与最终要求一致,只需遍历一遍检查即可),最坏时间复杂度为O(n2)(情况为数组顺序正好与最终要求完全相反例如原数组为降序最终要求为升序),平均时间复杂度为O(n2)(元素相当大时才可忽略系数、低阶、常数的影响)
空间时间复杂度为O(1)(因没有新开辟空间,只是在原有数组的基础上交换)。
冒泡排序为稳定性排序和原地排序。
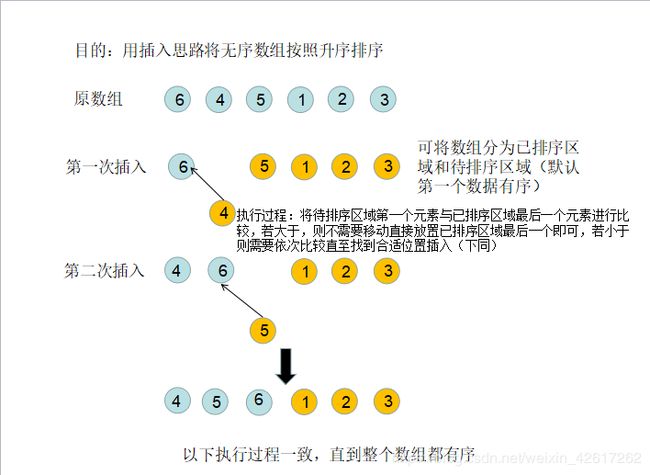
插入排序
1.直接插入排序:基于有序数组元素内容的插入得来。
做题思路:首先需要找到元素插入位置,再将元素插入即可。
核心步骤:将数组分为已排序区间和待排序区间(默认第一个元素为有序的,后面其他元素为无序)。若按照升序排序,则需将待排序区间第一个元素与已排序区间最后一个元素进行大小比较,若大于,则不需移动成为已排序区间最后一个元素即可;若小于,则需要将待排序区间第一个元素(插入元素)挨个从后向前对比已排序区间元素,直至找到合适位置插入即可。
核心步骤图解:
插入排序源代码:
public class Test {
public static void main(String[] args) {
int[] data=new int[]{6,4,5,1,2,3};
insertSort(data);
for(int i:data){
System.out.print(i+" ");
}
}
public static void insertSort(int[] data){//直接插入排序算法
int n=data.length;
if(n<=1){//判断若数组为空或只有一个元素时直接返回即可
return;
}
for(int i=1;i<n;i++){//外层循环控制循环次数(下标从1开始是因为默认第一个元素有序,此循环区间为待排序区间)
int value=data[i];//插入元素
//内层循环控制两元素对比次数(下标从已排序区间最后一个元素开始从后向前遍历)
int j=i-1;
for(;j>=0;j--){
if(value<data[j]){
data[j+1]=data[j];//若插入元素小于已排序元素,则需要向前移动,即相当于已排序元素向后移动
}else{//若插入元素大于已排序某元素直接跳出
break;
}
}
data[j+1]=value;//将元素插入(此时j+1是因为上面循环退出时j--之后判断)
}
}
}
我们通过代码可以看出直接插入排序最好排序时间复杂度为O(n)(情况为数组正好与最终要求一致,只需遍历一遍检查即可),最坏时间复杂度为O(n2)(情况为数组顺序正好与最终要求完全相反例如原数组为降序最终要求为升序),平均时间复杂度为O(n2)(元素相当大时才可忽略系数、低阶、常数的影响)
空间时间复杂度为O(1)(因没有新开辟空间,只是在原有数组的基础上交换)。
直接插入排序为稳定性排序和原地排序。
那么冒泡排序和直接插入排序相比哪个应用更广、效率更高呢?
我们按照开头判断排序算法效率的方法来看,时间复杂度空间复杂度两者均相同,故我们可看元素之间的交换次数。我们通过分析可知冒泡排序每次均要进行两个相邻元素之间的对比交换,而直接插入排序交换次数明显较少。故直接插入排序算法应用更广、效率更高。
测试代码:
import java.util.Random;
public class Test {
public static void main(String[] args) {
int[] data=generateRandomArray(8000,1000,10000);
bubbleSort(data);
insertSort(data);
}
public static void insertSort(int[] data){
long startTime=System.currentTimeMillis();
int n=data.length;
if(n<=1){
return;
}
for(int i=1;i<n;i++){
int value=data[i];
int j=i-1;
for(;j>=0;j--){
if(value<data[j]){
data[j+1]=data[j];
}else{
break;
}
}
data[j+1]=value;
}
long endTime=System.currentTimeMillis();
long time=endTime-startTime;
System.out.println("直接插入:"+time+"毫秒");
}
public static void bubbleSort(int[] data){
long starttime=System.currentTimeMillis();
int n=data.length;
if(n<=1){
return;
}
for(int i=0;i<n;i++){
boolean flag=false;
for(int j=0;j<n-i-1;j++){
if(data[j]>data[j+1]){
flag=true;
data[j]^=data[j+1];
data[j+1]^=data[j];
data[j]^=data[j+1];
}
}
if(!flag){
break;
}
}
long endtime=System.currentTimeMillis();
long time=endtime-starttime;
System.out.println("冒泡:"+time+"毫秒");
}
public static int[] generateRandomArray(int n,int rangeL,int rangeR){
if(rangeL>rangeR){
throw new IndexOutOfBoundsException("越界异常");
}
int[] arr=new int[n];
for(int i=0;i<n;i++){
arr[i]=new Integer(new Random().nextInt(rangeR-rangeL+1)+rangeL);
}
return arr;
}
}