LSTM回归比特币价格

参考教程：
https://www.youtube.com/watch?v=nMLPYT_SMRo
https://www.youtube.com/watch?v=V-pvtUThhNE

库导入与超参数设定

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

BATCH_START = 0
TIME_STEPS = 20
BATCH_SIZE = 50
INPUT_SIZE = 1
OUTPUT_SIZE = 1
CELL_SIZE = 10
LR = 0.02

数据预处理

df = pd.read_excel('BTCUSDT_min_5.xlsx')  # 读入比特币价格数据
data = np.array(df['close'])  # 获取收盘价序列

normalize_data = (data - np.mean(data)) / np.std(data)  # 标准化
normalize_data = normalize_data[:, np.newaxis]  # 增加维度

train = []  # 训练集
for i in range(len(normalize_data) - TIME_STEPS - 1):
    x = normalize_data[i:i + TIME_STEPS]
    train.append(x.tolist())


def get_batch():
    global BATCH_START, TIME_STEPS
    xs = np.arange(BATCH_START, BATCH_START + TIME_STEPS * BATCH_SIZE).reshape(BATCH_SIZE, TIME_STEPS) / 8
    seq = np.ones([BATCH_SIZE, TIME_STEPS]) * 1.5
    res = np.array(train[BATCH_START:BATCH_START + BATCH_SIZE]).reshape(BATCH_SIZE, TIME_STEPS)
    BATCH_START += TIME_STEPS
    return [seq[:, :, np.newaxis], res[:, :, np.newaxis], xs]

定义RNN

class LSTMRNN(object):
    def __init__(self, n_steps, input_size, output_size, cell_size, batch_size):
        self.n_steps = n_steps
        self.input_size = input_size
        self.output_size = output_size
        self.cell_size = cell_size
        self.batch_size = batch_size
        with tf.name_scope('inputs'):
            self.xs = tf.placeholder(tf.float32, [None, n_steps, input_size], name='xs')
            self.ys = tf.placeholder(tf.float32, [None, n_steps, output_size], name='ys')
        with tf.variable_scope('in_hidden'):
            self.add_input_layer()
        with tf.variable_scope('LSTM_cell'):
            self.add_cell()
        with tf.variable_scope('out_hidden'):
            self.add_output_layer()
        with tf.name_scope('cost'):
            self.compute_cost()
        with tf.name_scope('train'):
            self.train_op = tf.train.AdamOptimizer(LR).minimize(self.cost)

    def add_input_layer(self, ):
        l_in_x = tf.reshape(self.xs, [-1, self.input_size], name='2_2D')  # (batch*n_step, in_size)
        # Ws (in_size, cell_size)
        Ws_in = self._weight_variable([self.input_size, self.cell_size])
        # bs (cell_size, )
        bs_in = self._bias_variable([self.cell_size, ])
        # l_in_y = (batch * n_steps, cell_size)
        with tf.name_scope('Wx_plus_b'):
            l_in_y = tf.matmul(l_in_x, Ws_in) + bs_in
        # reshape l_in_y ==> (batch, n_steps, cell_size)
        self.l_in_y = tf.reshape(l_in_y, [-1, self.n_steps, self.cell_size], name='2_3D')

    def add_cell(self):
        lstm_cell = tf.contrib.rnn.BasicLSTMCell(self.cell_size, forget_bias=1.0, state_is_tuple=True)
        with tf.name_scope('initial_state'):
            self.cell_init_state = lstm_cell.zero_state(self.batch_size, dtype=tf.float32)
        self.cell_outputs, self.cell_final_state = tf.nn.dynamic_rnn(
            lstm_cell, self.l_in_y, initial_state=self.cell_init_state, time_major=False)

    def add_output_layer(self):
        # shape = (batch * steps, cell_size)
        l_out_x = tf.reshape(self.cell_outputs, [-1, self.cell_size], name='2_2D')
        Ws_out = self._weight_variable([self.cell_size, self.output_size])
        bs_out = self._bias_variable([self.output_size, ])
        # shape = (batch * steps, output_size)
        with tf.name_scope('Wx_plus_b'):
            self.pred = tf.matmul(l_out_x, Ws_out) + bs_out

    def compute_cost(self):
        losses = tf.contrib.legacy_seq2seq.sequence_loss_by_example(
            [tf.reshape(self.pred, [-1], name='reshape_pred')],
            [tf.reshape(self.ys, [-1], name='reshape_target')],
            [tf.ones([self.batch_size * self.n_steps], dtype=tf.float32)],
            average_across_timesteps=True,
            softmax_loss_function=self.ms_error,
            name='losses'
        )
        with tf.name_scope('average_cost'):
            self.cost = tf.div(
                tf.reduce_sum(losses, name='losses_sum'),
                self.batch_size,
                name='average_cost')
            tf.summary.scalar('cost', self.cost)

    @staticmethod
    def ms_error(labels, logits):
        return tf.square(tf.subtract(labels, logits))

    def _weight_variable(self, shape, name='weights'):
        initializer = tf.random_normal_initializer(mean=0., stddev=1., )
        return tf.get_variable(shape=shape, initializer=initializer, name=name)

    def _bias_variable(self, shape, name='biases'):
        initializer = tf.constant_initializer(0.1)
        return tf.get_variable(name=name, shape=shape, initializer=initializer)

主函数与可视化

if __name__ == '__main__':
    model = LSTMRNN(TIME_STEPS, INPUT_SIZE, OUTPUT_SIZE, CELL_SIZE, BATCH_SIZE)
    sess = tf.Session()
    merged = tf.summary.merge_all()
    writer = tf.summary.FileWriter("logs", sess.graph)
    init = tf.global_variables_initializer()
    sess.run(init)

    plt.show()
    for i in range(400):
        seq, res, xs = get_batch()
        if i == 0:
            feed_dict = {
                model.xs: seq,
                model.ys: res,
                # create initial state
            }
        else:
            feed_dict = {
                model.xs: seq,
                model.ys: res,
                model.cell_init_state: state  # use last state as the initial state for this run
            }

        _, cost, state, pred = sess.run(
            [model.train_op, model.cost, model.cell_final_state, model.pred],
            feed_dict=feed_dict)

        # plotting
        plt.plot(xs[0, :], res[0].flatten(), 'r', xs[0, :], pred.flatten()[:TIME_STEPS], 'b--')
        plt.ylim((0.8, 3.0))
        plt.draw()
        plt.pause(0.3)

        if i % 20 == 0:
            print('cost: ', round(cost, 4))
            result = sess.run(merged, feed_dict)
            writer.add_summary(result, i)

说明

1.对读入数据进行了标准化
2.将价格数据传入res，用seq对其进行拟合

最终效果

LearningRate=0.006时

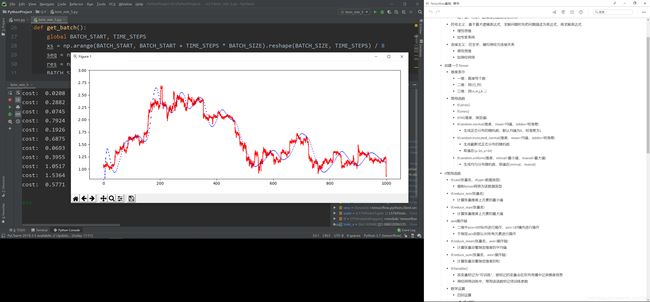
LearningRate=0.02时

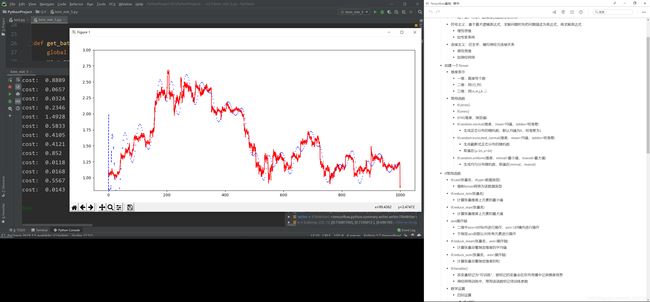
学习心得

1. 创建多个RNN时，要注意命名空间的使用
2. 在为seq选择具体函数时，一开始考虑到价格波动的周期性，尝试使用sin函数进行拟合，但会受到sin自身周期的较大影响，最终效果不好，主要表现在两个方面：（1）大波动无法及时更新变化；（2）小波动完全按照sin固有周期波动
3. 将seq设置为可训练参数，出现batch内过拟合，总体趋势又欠拟合
4. 最终选择将seq设置为固定值为1.5的直线，并适当调整了LearningRate，效果相较于前两者有较大提升，但出现batch内欠拟合，且总体趋势反映有一定迟缓