贪心(婪)算法之哈夫曼编码(Huffman code)学习笔记（Python版）

前言（可省略。）：
哈夫曼编码可以很有效的压缩数据：通常可以节省 20%~90%的空间，具体压缩率依赖于数据的特性。我们将待压缩数据看做字符序列。根据每个字符的出现频率，哈夫曼贪心算法构造出字符的最优二进制表示。

假定我们希望压缩一个10个字符的数据文件。下表给出了文件中所出现的字符和它们的出现频率。也就是说，文件中只出现了6个不同字符，其中字符a出现了45 000次。

	a	b	c	d	e	f
频率（千次）	45	13	12	16	9	5
定长编码	000	001	010	011	100	101
变长编码	0	101	100	111	1101	1100

• 一个字符编码的问题。一个100 000个字符的文件，只包含a~f 6个不同字符，出现的频率如上表。如果为每个字符指定一个3为的码字，我们可以将文件编码为300 000位的长度。但使用上表的变长编码，我们可以仅用224 000位编码文件。因此我们看到这是文件的最优字符编码。

因此我们知道了哈夫曼编码。
哈夫曼编码是可变字长编码的一种。
哈夫曼设计了一个贪心算法来构造最优前缀码，被称为哈夫曼编码（Huffman code）。哈夫曼树：哈夫曼树又称最优二叉树。它是 n 个带权叶子结点构成的所有二叉树中，带权路径长度 WPL 最小的二叉树。

接下来我们来了解哈夫曼算法的具体过程

Note:每次构造二叉树时已按字母频率递增顺序排好序
步骤：每次构造二叉树将频率低的两棵树进行合并
1.我们借用上面的例子得到初始字母叶节点：

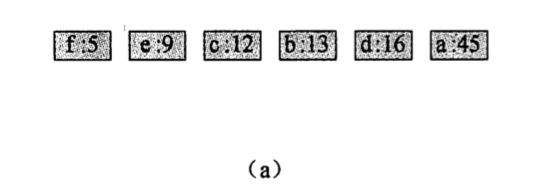
2.f 和 e 合并：

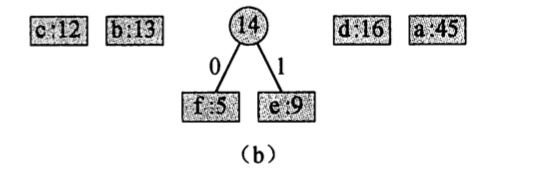
3.c 和 b 合并：

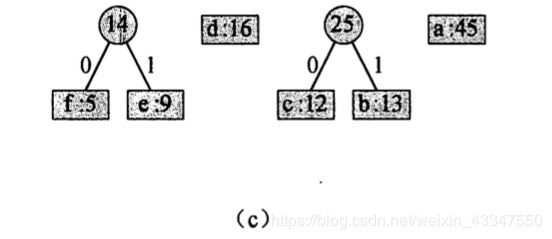
4. 14 和 d 合并：

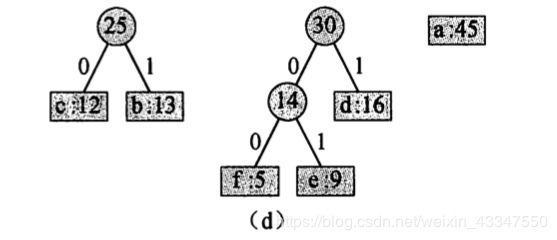
5. 25 和 30 合并：

6. 45 和 55 合并，最终得到完整的赫夫曼树：

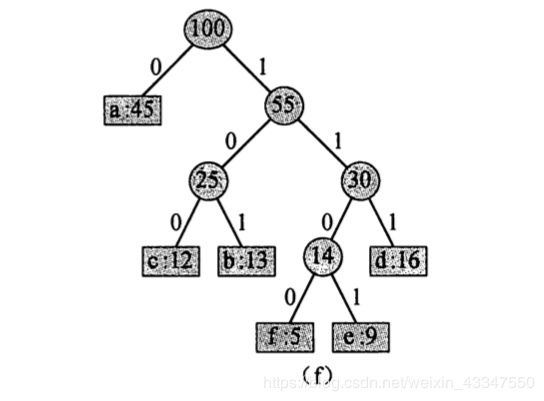
因此得到哈夫曼编码为：
a 的编码为： 0
b 的编码为： 101
c 的编码为： 100
d 的编码为： 111
e 的编码为： 1101
f 的编码为： 1100

代码实现哈夫曼编码

1.制备每个字符的概率表

def findTheCharFrequency(text):                                   
    result = dict()                                               
    with open(text,'r') as f:                                     
        for line in f.readlines():                                
            line = line.lower()                                   
            for i in line:                                        
                if i.isalpha():     #判断字符是否为英文字母                  
                    if i in result:                               
                        result[i] += 1                            
                    else:                                         
                        result.update({i:1})                      
    return result                                                 

存放字符的文本：

输出样例（以字典的形式给出每个字符的频率）：

{'t': 22, 'x': 3, 'h': 28, 'u': 16, 'f': 34, 'm': 20, 'a': 26, 'n': 24, 'c': 18, 'o': 24, 'd': 14, 'i': 20, 'g': 8, 's': 20, 'e': 32, 'p': 8, 'r': 18, 'y': 2, 'b': 2, 'l': 2, 'w': 2}

2.创建节点类

class Node(object):         
    def __init__(self, name=None, value=None):
        self.name = name    
        self.value = value  
        self.lchild = None  
        self.rchild = None  

3.以节点反向建立Huffman树

#创建Huffman树                                                                  
class HuffmanTree(object):                                                   
    #根据Huffman树的思想：以节点为基础，反向建立Huffman树                                       
    def __init__(self, char_Weights):                                        
        self.Leaf = [Node(k,v) for k, v in char_Weights.items()]             
        while len(self.Leaf) != 1:                                           
            self.Leaf.sort(key=lambda node:node.value, reverse=True)         
            n = Node(value=(self.Leaf[-1].value + self.Leaf[-2].value))      
            n.lchild = self.Leaf.pop(-1)                                     
            n.rchild = self.Leaf.pop(-1)                                     
            self.Leaf.append(n)                                              
        self.root = self.Leaf[0]                                             
        self.Buffer = list(range(10))                                   

用递归地思想生成编码

    def Hu_generate(self, tree, length):
        node = tree
        if (not node):
            return
        elif node.name:
            print(node.name + ' 的Huffman编码为: ', end='')
            for i in range(length):
                print(self.Buffer[i], end='')
            print('\n')
            return
        self.Buffer[length] = 0
        self.Hu_generate(node.lchild, length + 1)
        self.Buffer[length] = 1
        self.Hu_generate(node.rchild, length + 1)

输出哈夫曼编码

    def get_code(self):
        self.Hu_generate(self.root, 0)

输出

if __name__=='__main__':
    text = r'123.txt'
    result = findTheCharFrequency(text)
    print(result)
    tree = HuffmanTree(result)
    tree.get_code()

输出样例：

e 的Huffman编码为: 000
f 的Huffman编码为: 001
r 的Huffman编码为: 0100
c 的Huffman编码为: 0101
s 的Huffman编码为: 0110
i 的Huffman编码为: 0111
m 的Huffman编码为: 1000
t 的Huffman编码为: 1001
o 的Huffman编码为: 1010
n 的Huffman编码为: 1011
w 的Huffman编码为: 1100000
l 的Huffman编码为: 1100001
x 的Huffman编码为: 1100010
b 的Huffman编码为: 11000110
y 的Huffman编码为: 11000111
d 的Huffman编码为: 11001
a 的Huffman编码为: 1101
h 的Huffman编码为: 1110
p 的Huffman编码为: 111100
g 的Huffman编码为: 111101
u 的Huffman编码为: 11111

完整代码：

#制备每个字符的概率表
def findTheCharFrequency(text):
    result = dict()
    with open(text,'r') as f:
        for line in f.readlines():
            line = line.lower()
            for i in line:
                if i.isalpha():     #判断字符是否为英文字母
                    if i in result:
                        result[i] += 1
                    else:
                        result.update({i:1})
    return result

#创建节点类
class Node(object):
    def __init__(self, name=None, value=None):
        self.name = name
        self.value = value
        self.lchild = None
        self.rchild = None

#创建Huffman树
class HuffmanTree(object):
    #根据Huffman树的思想：以节点为基础，反向建立Huffman树
    def __init__(self, char_Weights):
        self.Leaf = [Node(k,v) for k, v in char_Weights.items()]
        while len(self.Leaf) != 1:
            self.Leaf.sort(key=lambda node:node.value, reverse=True)
            n = Node(value=(self.Leaf[-1].value + self.Leaf[-2].value))
            n.lchild = self.Leaf.pop(-1)
            n.rchild = self.Leaf.pop(-1)
            self.Leaf.append(n)
        self.root = self.Leaf[0]
        self.Buffer = list(range(10))

    #用递归地思想生成编码
    def Hu_generate(self, tree, length):
        node = tree
        if (not node):
            return
        elif node.name:
            print(node.name + ' 的Huffman编码为: ', end='')
            for i in range(length):
                print(self.Buffer[i], end='')
            print('\n')
            return
        self.Buffer[length] = 0
        self.Hu_generate(node.lchild, length + 1)
        self.Buffer[length] = 1
        self.Hu_generate(node.rchild, length + 1)

    #输出哈夫曼编码
    def get_code(self):
        self.Hu_generate(self.root, 0)

if __name__=='__main__':
    text = r'123.txt'
    result = findTheCharFrequency(text)
    #print(result)
    tree = HuffmanTree(result)
    tree.get_code()

---

本篇完