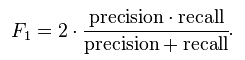气象上常见评分函数及其python实现

气象上常见评分函数及其python实现

1 简介

气象部门在发布预报时，发布的是一定区域范围的网格化(或站点化)的气象要素结果，以降水预报为例，

• 先将预报区域划分为60 * 60(视空间分辨率而定，空间分辨率越高，格点数值越大) 的网格，每个网格上都存在对应的降水预报值。
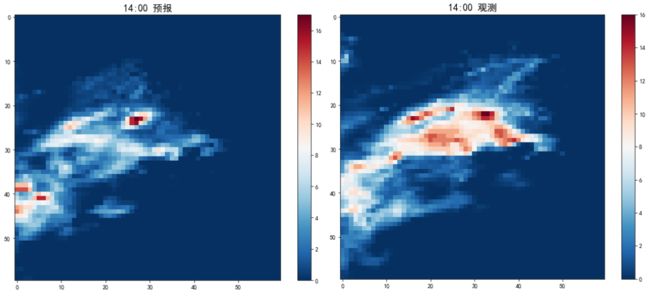
• 事后需要对预测结果进行检验，如图1，左图为14时的预报结果y_pre，右图为真实观测结果y_obs，异同明显。那如何衡量预报好坏呢？即如何衡量预报场(y_pre) 与 观测场(真值y_obs) 的异同程度呢?
• 主要采取二分类思想进行评价。但针对不同需求，气象上有许多预报准确度评价指标。
  
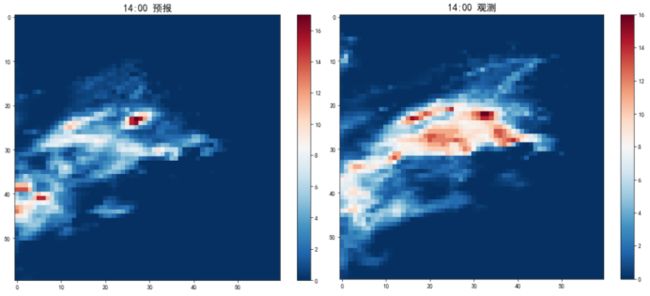
  ​ 图1 14时的降水预测与观测值对比

2 评价指标及其python实现

2.1 二分类介绍

假设有两个类别，正和负，分别用1，0表示，如下表格。

	预测 负例	预测 正例
真实 负例	TN(True negative)	FP(False positive)
真实 正例	FN(False negative)	TP(True positive)

该表格称为 混淆矩阵(confusion matrix)。

• TN : 真阴性。实际为0，预测为0.

• TP : 真阳性。实际为1，预测为1.

• FP: 假阳性。实际为0，预测为1.

• FN: 假阴性。 实际为1，预测为0.

• 召回率(Recall)：R=TP/(TP+FN) ，指的是被预测为正例的占总的正例的比重；

• 精准度(precision)：P = TP/(TP+FP) ，指被分类器判定正例中的正样本的比重；

• 准确率(Accuracy)：A = (TP+TN)/(TP+FN+FP+TN) ，反映了分类器对整个样本的判定能力，也就是说能将正

  的判定为正，负的判定为负。

• F1为：
  

在实际应用中，我们不仅希望Accuracy高，还希望模型对每个类别都有很强的分类能力，即recall 和 precision都要高。

2.2 降水评价

2.2.1 气象二分类指标

气象上的降水评价指标基本都建立在二分类基础上。

以上面的y_pre 和 y_obs 为例，共计有3600个格点，选定一个阈值rain_threshold ，格点数值 >= rain_threshold 即为正例， 否则为负例。这里采取晴雨分类，即rain_threshold = 0.1

构建混淆矩阵，晴为负例，雨为正例，如下：

	预测 晴	预测 雨
真实 晴	TN: 1968	FP: 52	2020
真实 雨	FN: 458	TP: 1122	1580
	2426	1174

• Recall: R=TP/(TP+FN) = 1122/(1122 + 458) = 0.71

• precision: p = TP/(TP + FP) = 1122/(1122 + 52) = 0.95

• Accuracy: (TP + TN)/(TN + FP + FN + TP) = 0.86

类比到气象上，概念一致，只是换了名称。

	预测 晴	预测 雨
真实 晴	correctnegatives	falsealarms(误警)	2020
真实 雨	misses(漏报)	hits(击中)	1580
	2426	1174

代码如下：

def prep_clf(obs,pre, threshold=0.1):
    '''
    func: 计算二分类结果-混淆矩阵的四个元素
    inputs:
        obs: 观测值，即真实值；
        pre: 预测值；
        threshold: 阈值，判别正负样本的阈值,默认0.1,气象上默认格点 >= 0.1才判定存在降水。
    
    returns:
        hits, misses, falsealarms, correctnegatives
        #aliases: TP, FN, FP, TN 
    '''
    #根据阈值分类为 0, 1
    obs = np.where(obs >= threshold, 1, 0)
    pre = np.where(pre >= threshold, 1, 0)

    # True positive (TP)
    hits = np.sum((obs == 1) & (pre == 1))

    # False negative (FN)
    misses = np.sum((obs == 1) & (pre == 0))

    # False positive (FP)
    falsealarms = np.sum((obs == 0) & (pre == 1))

    # True negative (TN)
    correctnegatives = np.sum((obs == 0) & (pre == 0))

    return hits, misses, falsealarms, correctnegatives


def precision(obs, pre, threshold=0.1):
    '''
    func: 计算精确度precision: TP / (TP + FP)
    inputs:
        obs: 观测值，即真实值；
        pre: 预测值；
        threshold: 阈值，判别正负样本的阈值,默认0.1,气象上默认格点 >= 0.1才判定存在降水。
    
    returns:
        dtype: float
    '''

    TP, FN, FP, TN = prep_clf(obs=obs, pre = pre, threshold=threshold)

    return TP / (TP + FP)


def recall(obs, pre, threshold=0.1):
    '''
    func: 计算召回率recall: TP / (TP + FN)
    inputs:
        obs: 观测值，即真实值；
        pre: 预测值；
        threshold: 阈值，判别正负样本的阈值,默认0.1,气象上默认格点 >= 0.1才判定存在降水。
    
    returns:
        dtype: float
    '''

    TP, FN, FP, TN = prep_clf(obs=obs, pre = pre, threshold=threshold)

    return TP / (TP + FN)


def ACC(obs, pre, threshold=0.1):
    '''
    func: 计算准确度Accuracy: (TP + TN) / (TP + TN + FP + FN)
    inputs:
        obs: 观测值，即真实值；
        pre: 预测值；
        threshold: 阈值，判别正负样本的阈值,默认0.1,气象上默认格点 >= 0.1才判定存在降水。
    
    returns:
        dtype: float
    '''

    TP, FN, FP, TN = prep_clf(obs=obs, pre = pre, threshold=threshold)

    return (TP + TN) / (TP + TN + FP + FN)

def FSC(obs, pre, threshold=0.1):
    '''
    func:计算f1 score = 2 * ((precision * recall) / (precision + recall))
    '''
    precision_socre = precision(obs, pre, threshold=threshold)
    recall_score = recall(obs, pre, threshold=threshold)

    return 2 * ((precision_socre * recall_score) / (precision_socre + recall_score))

由以上四个基本指标，引申出许多气象降水评价指标。

有一点需要注意：气象上的降水评价指标基本都建立在二分类基础上，即任何指标都必须指明rain_threshold。

2.2.2 TS评分 & CSI

1 物理概念

• TS：风险评分ThreatScore;

• CSI: critical success index 临界成功指数;

• 两者的物理概念完全一致。

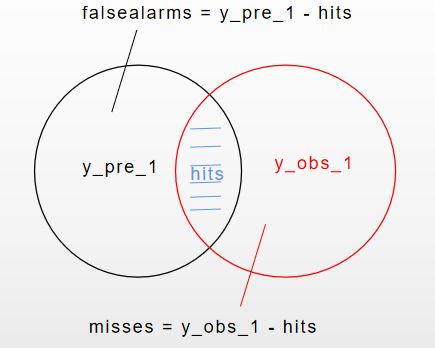
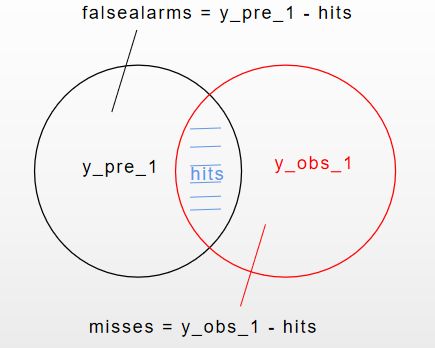
• 如下图：y_pre_1为预测的降水区( >= threshold，下同)，y_obs_1为观测的降水区，hits为两者交界区，
  TS = hits/(hits + falsealarms + misses) 。其中falsealarms = y_pre_1 - hits, misses = y_obs_1 - hits。

2 代码

def TS(obs, pre, threshold=0.1):
    
    '''
    func: 计算TS评分: TS = hits/(hits + falsealarms + misses) 
    	  alias: TP/(TP+FP+FN)
    inputs:
        obs: 观测值，即真实值；
        pre: 预测值；
        threshold: 阈值，判别正负样本的阈值,默认0.1,气象上默认格点 >= 0.1才判定存在降水。
    returns:
        dtype: float
    '''

    hits, misses, falsealarms, correctnegatives = prep_clf(obs=obs, pre = pre, threshold=threshold)

    return hits/(hits + falsealarms + misses) 

2.2.3 公平技巧评分(ETS)

1 物理概念

• 公平技巧评分(Equitable Threat Score, ETS)用于衡量对流尺度集合预报的预报效果。ETS评分表示在预报区域内满足某降水阈值的降水预报结果相对于满足同样降水阈值的随机预报的预报技巧；

• ETS评分是对TS评分的改进，能对空报或漏报进行惩罚，使评分相对后者更加公平.

2 代码

def ETS(obs, pre, threshold=0.1):
    '''
    ETS - Equitable Threat Score
    details in the paper:
    Winterrath, T., & Rosenow, W. (2007). A new module for the tracking of
    radar-derived precipitation with model-derived winds.
    Advances in Geosciences,10, 77–83. https://doi.org/10.5194/adgeo-10-77-2007
    Args:
        obs (numpy.ndarray): observations
        pre (numpy.ndarray): prediction
        threshold (float)  : threshold for rainfall values binaryzation
                             (rain/no rain)
    Returns:
        float: ETS value
    '''
    hits, misses, falsealarms, correctnegatives = prep_clf(obs=obs, pre = pre,
                                                           threshold=threshold)
    num = (hits + falsealarms) * (hits + misses)
    den = hits + misses + falsealarms + correctnegatives
    Dr = num / den

    ETS = (hits - Dr) / (hits + misses + falsealarms - Dr)

    return ETS

2.2.4 空报率(FAR)

1 物理概念

• False Alarm Rate 。在预报降水区域中实际没有降水的区域占总预报降水区域的比重。

• FAR = (y_pre_1 - hits)/y_pre_1 = falsealarms / (hits + falsealarms)

2 代码

def FAR(obs, pre, threshold=0.1):
    '''
    func: 计算误警率。falsealarms / (hits + falsealarms) 
    FAR - false alarm rate
    Args:
        obs (numpy.ndarray): observations
        pre (numpy.ndarray): prediction
        threshold (float)  : threshold for rainfall values binaryzation
                             (rain/no rain)
    Returns:
        float: FAR value
    '''
    hits, misses, falsealarms, correctnegatives = prep_clf(obs=obs, pre = pre,
                                                           threshold=threshold)

    return falsealarms / (hits + falsealarms)

2.2.5 漏报率(MAR)

1 物理概念

• Missing Alarm Rate。实际降水区域中漏报的区域占据全部实际降水区域的比重。
• MAR = (y_obs_1 - hits)/y_obs_1 = misses / (hits + misses)

2 代码

def MAR(obs, pre, threshold=0.1):
    '''
    func : 计算漏报率 misses / (hits + misses)
    MAR - Missing Alarm Rate
    Args:
        obs (numpy.ndarray): observations
        pre (numpy.ndarray): prediction
        threshold (float)  : threshold for rainfall values binaryzation
                             (rain/no rain)
    Returns:
        float: MAR value
    '''
    hits, misses, falsealarms, correctnegatives = prep_clf(obs=obs, pre = pre,
                                                           threshold=threshold)

    return misses / (hits + misses)

2.2.6 命中率(POD)

1 物理概念

• Probability of Detection。即预测出的实际的降水区域占据全部实际降水区域的比重。
• POD = hits / y_obs_1 = hits / (hits + misses) = 1- MAR

2 代码

def POD(obs, pre, threshold=0.1):
    '''
    func : 计算命中率 hits / (hits + misses)
    pod - Probability of Detection
    Args:
        obs (numpy.ndarray): observations
        pre (numpy.ndarray): prediction
        threshold (float)  : threshold for rainfall values binaryzation
                             (rain/no rain)
    Returns:
        float: PDO value
    '''
    hits, misses, falsealarms, correctnegatives = prep_clf(obs=obs, pre = pre,
                                                           threshold=threshold)

    return hits / (hits + misses)

2.2.7 偏差评分(Bia score)

1 物理概念

• 偏差评分(Bias score)主要用来衡量模式对某一量级降水的预报偏差, 该评分在数值上等于预报区域内满足某降水阈值的总格点数与对应实况降水总格点数的比值(Kong et al, 2008)。用来反映降水总体预报效果的检验方法。
• Bias = y_pred_1/y_obs_1 = (hits + falsealarms)/(hits + misses)

2 代码

def BIAS(obs, pre, threshold = 0.1):
    '''
    func: 计算Bias评分: Bias =  (hits + falsealarms)/(hits + misses) 
    	  alias: (TP + FP)/(TP + FN)
    inputs:
        obs: 观测值，即真实值；
        pre: 预测值；
        threshold: 阈值，判别正负样本的阈值,默认0.1,气象上默认格点 >= 0.1才判定存在降水。
    returns:
        dtype: float
    '''    
    hits, misses, falsealarms, correctnegatives = prep_clf(obs=obs, pre = pre,
                                                           threshold=threshold)

    return (hits + falsealarms) / (hits + misses)

2.2.8 其他评分

1. HSS

HSS公式如下：

def HSS(obs, pre, threshold=0.1):
    '''
    HSS - Heidke skill score
    Args:
        obs (numpy.ndarray): observations
        pre (numpy.ndarray): pre
        threshold (float)  : threshold for rainfall values binaryzation
                             (rain/no rain)
    Returns:
        float: HSS value
    '''
    hits, misses, falsealarms, correctnegatives = prep_clf(obs=obs, pre = pre,
                                                           threshold=threshold)

    HSS_num = 2 * (hits * correctnegatives - misses * falsealarms)
    HSS_den = (misses**2 + falsealarms**2 + 2*hits*correctnegatives +
               (misses + falsealarms)*(hits + correctnegatives))

    return HSS_num / HSS_den

2. BSS

def BSS(obs, pre, threshold=0.1):
    '''
    BSS - Brier skill score
    Args:
        obs (numpy.ndarray): observations
        pre (numpy.ndarray): prediction
        threshold (float)  : threshold for rainfall values binaryzation
                             (rain/no rain)
    Returns:
        float: BSS value
    '''
    obs = np.where(obs >= threshold, 1, 0)
    pre = np.where(pre >= threshold, 1, 0)

    obs = obs.flatten()
    pre = pre.flatten()

    return np.sqrt(np.mean((obs - pre) ** 2))

3. MAE

def MAE(obs, pre):
    """
    Mean absolute error
    Args:
        obs (numpy.ndarray): observations
        pre (numpy.ndarray): prediction
    Returns:
        float: mean absolute error between observed and simulated values
    """
    obs = pre.flatten()
    pre = pre.flatten()

    return np.mean(np.abs(pre - obs))

4. RMSE

def RMSE(obs, pre):
    """
    Root mean squared error
    Args:
        obs (numpy.ndarray): observations
        pre (numpy.ndarray): prediction
    Returns:
        float: root mean squared error between observed and simulated values
    """
    obs = obs.flatten()
    pre = pre.flatten()

    return np.sqrt(np.mean((obs - pre) ** 2))

2.2.9 阈值选取

• 上述评分都与阈值threshold密切相关，我们关注什么类型降水的预报准确度，就使用对应的threshold。

threshold : mm	0.1	10	25	50	100
降雨类型	小雨	中雨	大雨	暴雨	特大暴雨

3 应用举例

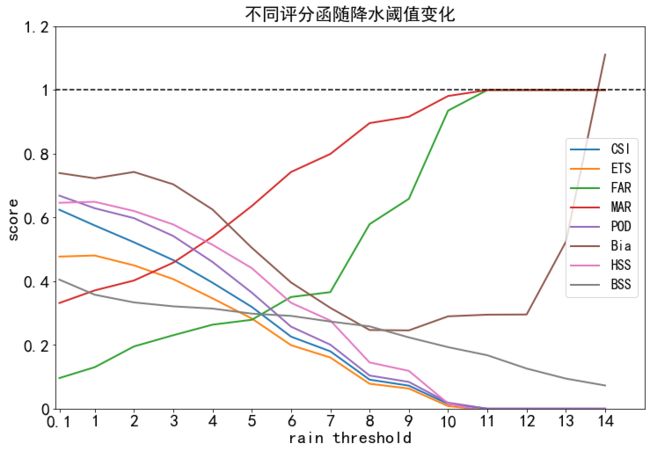
选取上述例子，来看在不同阈值下各评分函数数值。

• 除Bia外，其他评分函数数值范围都在**[0,1]之间**；其中FAR \ MAR越低越好，其他越高越好。
• 实际情况：FAR和 MAR一般随着降水阈值增大而显著增加，CSI 、ETS、POD、HSS、BSS随阈值增大而减小。 即该预报模式对强降水的预报能力较弱，对是否降水预测更准确。

在真实的检验中，y_obs并不是均匀网格的，而是站点分布的，依据相同思路，比较区域内的所有站点预测和站点观测值，也能得到对应评分。

4 参考文献

rainymotion v0.1 github

分类模型评估指标——准确率、精准率、召回率、F1、ROC曲线、AUC曲线

王在文,梁旭东,范水勇,等. 数值模式降水评分对分辨率的敏感性初探[J].暴雨灾害，2016,35(1):10-16

吴启树，韩美，刘铭，等．基于评分最优化的模式降水预报订正算法对比．应用气象学报，2017,28(3):306317.DOI: 10.11898/10017313.20170305

匡秋明,杨雪冰,张文生,何险峰,惠建忠.多源数据融合高时空分辨率晴雨分类.软件学报,2017,28(11):2925−

\2939. http://www.jos.org.cn/1000-9825/5336.htm