二叉树遍历(数据结构)
二叉树基本算法 遍历
- 一.任务要求
- 二 .二叉树示意图
- 三.遍历
- 四.算法
- 搭建二叉树
- 查找二叉树
- 用括号表示法输出二叉树
- 求二叉树结点个数
- 求二叉树叶子结点个数
- 销毁树
- 找一个结点的左右孩子
一.任务要求
设计程序,实现二叉树的基本运算,在此基础上,完成如下功能:
- 1、由二叉树创建对应的二叉链存储结构b,该二叉树的括号表示串为
-
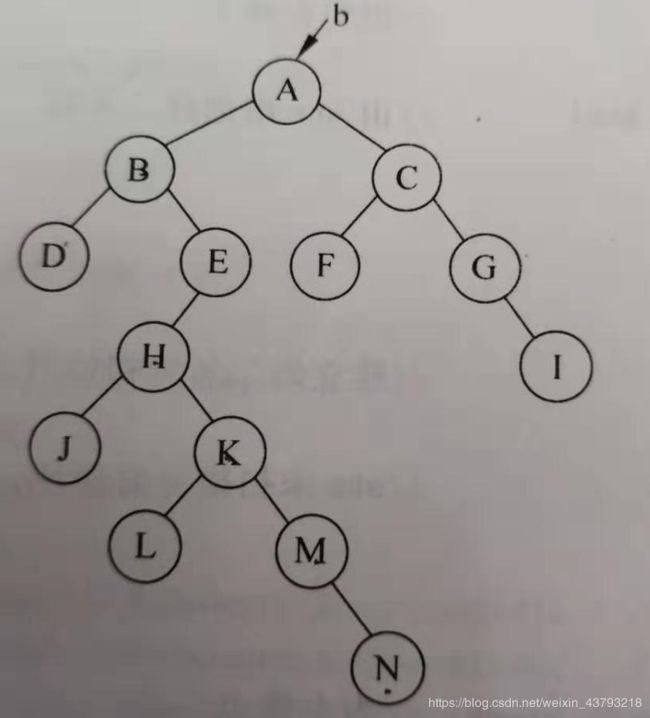
"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))"。 - 2、输出二叉树b
-
3、对创建的二叉树进行先序遍历 -
4、对创建的二叉树进行中序遍历 -
5、对创建的二叉树进行后序遍历 -
6、对创建的二叉树进行层次遍历 - 7、输出’B’结点的左、右孩子结点值
-
8、输出二叉树b的深度 -
9、输出二叉树b的宽度 -
10、输出二叉树b的结点个数 -
11、输出二叉树b的叶子结点个数 -
12、销毁二叉树
二 .二叉树示意图
三.遍历
二叉树最先想到的就是遍历,如何有效,快速的遍历输出呢,
我将二叉树的深度优先搜索算法与广义优先搜索算法都写了一遍,
发现果然还是递归比较简洁明了,而且后序遍历与前序遍历,中序遍历的非递归上有着明显差异。
我先引用一个伪代码来说明我的想法
void preOrder(TreeNode *T)
{
p = T
while(p不空||栈不空)
{
if(p不空){ //两种情况:1.栈不空;2.栈空
p入栈; (前序遍历,访问) 入p左子节点;
}else
{ //一种情况:当前节点为空,但栈不空
p=出栈; (中序遍历,访问) 入p右子节点;
}
}
}
void InOrder(BTNode *b){ //中序遍历
BTNode *stack[15];
int top = -1;
BTNode *p = b;
while(p!=NULL||top!=-1){
if(p!=NULL){
stack[++ top] = p;//中序遍历 访问结点 入栈
p = p->lchild;//继续访问下一个左结点
}else{
p = stack[top --];//中序遍历 访问结点 出栈
printf("%c ",p->data); //输出结点
p = p->rchild;//访问结点右孩子
}
}}后序遍历整体与前中序遍历过程相似。
但要注意,这时对于父节点的访问输出,需要在其右子树遍历完成的前提下进行。
所以不能像前中序遍历一样,在遍历完左子树后,就直接出栈。
我们需要利用这个未出栈的栈顶元素去获取右子树,
在遍历完右子树后,就可以出栈,并对此节点进行访问输出。
这里我们需要使用一个标记,以区分是从左子树取栈还是从右子树出栈
大致思想
从当前节点开始遍历:
- 若当前节点存在,就存入栈中,并且置节点flag为1(第一次访问),然后访问其左子树;
- 直到当前节点不存在,需要回退,这里有两种情况:
1)当栈顶节点flag为1时,则表明是从左子树回退,这时需置栈顶节点flag为2(第二次访问),然后通过栈顶节点访问其右子树(取栈顶节点用,但不出栈)
2)当栈顶节点flag为2时,则表明是从右子树回退,这时需出栈,并取出栈节点做访问输出。输出完毕需要置当前节点为空,以便继续回退。 - 不断重复12,直到当前节点不存在且栈空。后序遍历非递归 代码如下
void postOrder(TreeNode *T){
TreeNode *stack[15];
int top = -1;
int flagStack[15]; //记录每个节点访问次数栈
TreeNode *p = T;
while(p!=NULL||top!=-1){
if(p!=NULL){ //第一次访问,flag置1,入栈
stack[++ top] = p;
flagStack[top] = 1;
p = p->lChild;
}
else{//(p == NULL)
if(flagStack[top] == 1){ //第二次访问,flag置2,取栈顶元素但不出栈
p = stack[top];
flagStack[top] = 2;
p = p->rChild;
}
else{ //第三次访问,出栈
p = stack[top --];
printf("%d\t",p->data); //出栈时,访问输出
p = NULL; //p置空,以便继续退栈
}
}
}
}四.算法
搭建二叉树
void CreateBTNode(BTNode *&b,char *str) //由str串创建二叉链
{
BTNode *St[MaxSize],*p=NULL;
int top=-1,k,j=0;
char ch;
b=NULL; //建立的二叉树初始时为空
ch=str[j];
while (ch!='\0') //str未扫描完时循环
{
switch(ch)
{
case '(':top++;St[top]=p;k=1; break; //为左节点
case ')':top--;break;
case ',':k=2; break; //为右节点
default:p=(BTNode *)malloc(sizeof(BTNode));
p->data=ch;p->lchild=p->rchild=NULL;
if (b==NULL) //p指向二叉树的根节点
b=p;
else //已建立二叉树根节点
{
switch(k)
{
case 1:St[top]->lchild=p;break;
case 2:St[top]->rchild=p;break;
}
}
}
j++;
ch=str[j];
}
}查找二叉树
BTNode *FindNode(BTNode *b,ElemType x) //返回data域为x的节点指针
{
BTNode *p;
if (b==NULL) return NULL;
else
if (b->data==x) return b;
else
{
p=FindNode(b->lchild,x);
if (p!=NULL) return p;
else return FindNode(b->rchild,x);
}
}求二叉树深度
int BTNodeDepth(BTNode *b) //求二叉树b的深度
{
int lchilddep,rchilddep;
if (b==NULL)
return(0); //空树的高度为0
else
{
lchilddep=BTNodeDepth(b->lchild); //求左子树的高度为lchilddep
rchilddep=BTNodeDepth(b->rchild); //求右子树的高度为rchilddep
return (lchilddep>rchilddep)? (lchilddep+1):(rchilddep+1);//子树高度加一(根的结点)
}
}用括号表示法输出二叉树
void DispBTNode(BTNode *b) //以括号表示法输出二叉树
{
if (b!=NULL)//不为空树时
{
printf("%c",b->data);
if (b->lchild!=NULL || b->rchild!=NULL)
{
printf("(");//还有结点时,括号包含下一层
DispBTNode(b->lchild);//递归
if (b->rchild!=NULL) printf(",");//(a,b)该结点的左右孩子
DispBTNode(b->rchild);
printf(")");
}
}
}求二叉树结点个数
int Nodes(BTNode *b) //求二叉树b的节点个数
{
int num1,num2;
if (b==NULL)//空树
return 0;
else if (b->lchild==NULL && b->rchild==NULL) //无后续结点
return 1;
else
{
num1=Nodes(b->lchild);
num2=Nodes(b->rchild);
return (num1+num2+1);//递归求结点数
}
}求二叉树叶子结点个数
int LeafNodes(BTNode *b) //求二叉树b的叶子节点个数
{
int num1,num2;
if (b==NULL)
return 0;
else if (b->lchild==NULL && b->rchild==NULL)
return 1;
else
{
num1=LeafNodes(b->lchild);
num2=LeafNodes(b->rchild);
return (num1+num2);//递归求不再有子树的结点个数
}
}销毁树
void DestroyBTNode(BTNode *&b)//销毁树
{
if (b!=NULL)
{
DestroyBTNode(b->lchild);
DestroyBTNode(b->rchild);
free(b);
}
}找一个结点的左右孩子
printf("\n (6) B节点:");//找到h结点的左右孩子
p=FindNode(b,'B');
if (p!=NULL)
{
lp=LchildNode(p);
if (lp!=NULL)
printf("左孩子为%c ",lp->data);
else
printf("无左孩子 ");
rp=RchildNode(p);
if (rp!=NULL)
printf("右孩子为%c",rp->data);
else
printf("无右孩子 ");
}