Python程序设计与科学计算精录&总结Episode.6 Python进阶:科学计算与科学计算库Numpy、SciPy(基于VS2019)
我觉得,类似的问题,两个不同的问法,意味着他们的学习习惯差距甚远。那就是:“想学的东西太多,没时间怎么办?”以及“想学的东西太多,很难坚持怎么办?”
如果是后者,学习这条路从来会很辛苦,但也很单纯,像初高中那种只需要考虑学习不需要考虑其它任何烦扰事情的日子是永远不会再有的。如果简单的事情都做不好,哪里还要祈求今后能做好更复杂的事情呢?
如果是前者,可以安静的时候自我思考,是否是盲目跟风学习,是否是过于零散的学习状态,是否急于求成?博主个人喜欢的学习方式,是以周为单位,专注于一件事情。这实际也是苹果公司运营及产品固守之道,优秀之源。同一周或者半月的时间,学好一样东西,做好一件事,别的东西都以完成及格的目标进行。至于周与周之间的计划则按照大的学习方向制定。这样的生活学习方式,可能上下课吃饭的时间都在疾走,的确忙碌,但一点也不忙乱。
一、Numpy基础简介:
1、什么是Numpy:
NumPy(Numerical Python) 是 Python 语言的一个扩展程序库,支持大量的维度数组与矩阵运算,此外也针对数组运算提供大量的数学函数库。
NumPy 的前身 Numeric 最早是由 Jim Hugunin 与其它协作者共同开发,2005 年,Travis Oliphant 在 Numeric 中结合了另一个同性质的程序库 Numarray 的特色,并加入了其它扩展而开发了 NumPy。NumPy 为开放源代码并且由许多协作者共同维护开发。
NumPy 是一个运行速度非常快的数学库,主要用于数组计算,包含:
- 一个强大的N维数组对象 ndarray
- 广播功能函数
- 整合 C/C++/Fortran 代码的工具
- 线性代数、傅里叶变换、随机数生成等功能
2、Numpy应用:
NumPy 通常与 SciPy(Scientific Python)和 Matplotlib(绘图库)一起使用, 这种组合广泛用于替代 MatLab,是一个强大的科学计算环境,有助于我们通过 Python 学习数据科学或者机器学习。
SciPy 是一个开源的 Python 算法库和数学工具包。
SciPy 包含的模块有最优化、线性代数、积分、插值、特殊函数、快速傅里叶变换、信号处理和图像处理、常微分方程求解和其他科学与工程中常用的计算。
Matplotlib 是 Python 编程语言及其数值数学扩展包 NumPy 的可视化操作界面。它为利用通用的图形用户界面工具包,如 Tkinter, wxPython, Qt 或 GTK+ 向应用程序嵌入式绘图提供了应用程序接口(API)。
3、ndarray中的对象属性:
ndarray中包含的函数/对象及其功能:
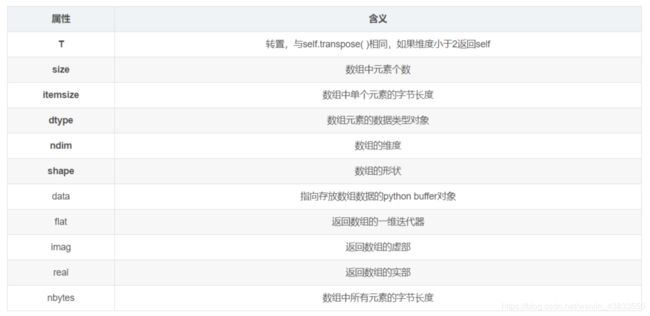
ndarray中的常用对象属性:
ndarray中的数据类型:
| bool_ | 布尔型数据类型(True 或者 False) |
| int_ | 默认的整数类型(类似于 C 语言中的 long,int32 或 int64) |
| intc | 与 C 的 int 类型一样,一般是 int32 或 int 64 |
| intp | 用于索引的整数类型(类似于 C 的 ssize_t,一般情况下仍然是 int32 或 int64) |
| int8 | 字节(-128 to 127) |
| int16 | 整数(-32768 to 32767) |
| int32 | 整数(-2147483648 to 2147483647) |
| int64 | 整数(-9223372036854775808 to 9223372036854775807) |
| uint8 | 无符号整数(0 to 255) |
| uint16 | 无符号整数(0 to 65535) |
| uint32 | 无符号整数(0 to 4294967295) |
| uint64 | 无符号整数(0 to 18446744073709551615) |
| float_ | float64 类型的简写 |
| float16 | 半精度浮点数,包括:1 个符号位,5 个指数位,10 个尾数位 |
| float32 | 单精度浮点数,包括:1 个符号位,8 个指数位,23 个尾数位 |
| float64 | 双精度浮点数,包括:1 个符号位,11 个指数位,52 个尾数位 |
| complex_ | complex128 类型的简写,即 128 位复数 |
| complex64 | 复数,表示双 32 位浮点数(实数部分和虚数部分) |
| complex128 | 复数,表示双 64 位浮点数(实数部分和虚数部分) |
了解了对象基本属性之后,我们来谈谈如何创建一个科学数组。
二、Numpy创建ndarray及简单应用:
1、ndarray的列表或元组转换创建方式:
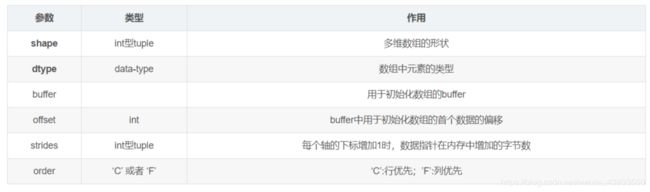
data=numpy.array(object, dtype=None, copy=True, order=None, subok=False, ndmin=0)
首先object代表输入对象的列表或者元组等,dtype表示数据类型,如果没给出则保存为所给列表或者元组中所需的最小类型。copy参数是布尔类型,默认True表示复制列表或者元组对象。order表示顺序。subok也是布尔类型,表示子类是否被传递。ndmin没什么实际的用处默认传递为0。
2、ndarray数字基础—矩阵:
首先需要知道数字矩阵的基础,就是零矩阵,单位阵和数量阵,它们分别代表了全部是0的矩阵、只有一个元素是1的矩阵和对角线上全是1的矩阵。这三种矩阵通过加减乘除可以构建所有我们需要的矩阵。
构建一个矩阵的语法:
data=numpy.mat("a11 a12 a13;a21 a22 a23;a31 a32 a33")
也就是利用分号隔开每行,利用空格隔开每个数字。或者利用array建立多维数组的方式来建立一个矩阵,其中逗号用于隔开行列表和各个数字:
data=numpy.array([a11,a12,a13], [a21,a22,a23], [a31,a32,a33])
此处注意!如果我们要建立单位阵,由于单位阵对角线为1的特性决定了它只能是方阵!
3、Numpy构建特殊数组:
某些时候,我们在创建数组之前已经确定了数组的维度以及各维度的长度。这时我们就可以使用numpy内建的一些函数来创建ndarray。例如:函数ones创建一个全1的数组、函数zeros创建一个全0的数组、函数empty创建一个内容随机或者为空的数组,在默认情况下,用这些函数创建的数组的类型都是float64,若需要指定数据类型,只需要闲置dtype参数即可。
上述三个函数还有三个从已知的数组中,创建shape相同的多维数组:ones_like、zeros_like、empty_like。
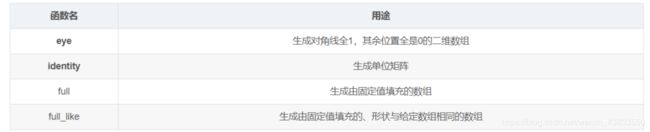
还有以下几个常用的创建函数:
以下我们对五种常用的函数的语法进行总结:
(1)ones函数系列:
data=numpy.ones(shape, dtype=None, order="C")
其中shape参数定义返回数组的形状,也就是维数,如(2,3)表示2X3矩阵,或者用单独数字表示。dtype参数是返回数组的数据类型,如numpy.int8或者默认的numpy.float64。order填写内存存储顺序是使用C语言的-row-major还是Fortan语言的-column-major,填写C或F字母即可。
如果需要创建多维数组,记得用ones_like对象。其中要想把一个上述语句创建好的线程的数组给转化成多维数组,只需要调用ones_like对象并且复制上述data即可,也就是:datamulti=numpy.(data)
(2)zeros函数系列:
data=numpy.zeros(shape, dtype=None, order="C")
语法和上面所说的ones一样,唯一的就是这个建立的是一个全零的数组,而ones是实现建立全1数组,功能不同。
如果需要创建多维数组,记得用zeros_like对象。
(3)empty函数系列:
data=numpy.empty(shape, dtype=None, order="C")
语法和上面所说的ones一样,唯一的就是这个建立的是一个空的数组,而ones是实现建立全1数组,功能不同。注意!全空数组和全零数组意义不一样,这个不难理解。
如果需要创建多维数组,记得用empty_like对象。
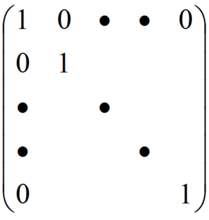
(4)eye函数系列:
data=numpy.eye(N, M=None, k=0, dtype=float)
其中,N是整数,返回数组行数,M是整数,返回数组的列数,如果不赋值默认与N一样是个方阵。k是整数,可选对角线的序列号,0对应主对角线,正数对应upper diagonal上三角,负数对应low diagonal下三角。dtype也就是返回数组数据类型同上。
(4)identity函数系列:
data=numpy.identity(n, dtype=None)
其中n是整数,返回方阵的行列数,dtype设定返回数据类型同上。identity对象函数实现的是快速生成一个单位方阵的功能,为了代码简洁同来替代eye函数再好不过了。
三、Numpy切片索引:
1、对于一维的ndarray可以使用python访问内置list的方式进行访问:整数索引、切片、迭代等方式
关于ndarray切片,与内置list切片类似,形式:
array[beg:end:slice]
其中参数的意义是:beg: 开始索引,end: 结束索引(不包含这个元素),step: 间隔
需要注意的是:
①beg可以为空,表示从索引0开始;
②end也可以为空,表示达到索引结束(包含最后一个元素);
③step为空,表示间隔为1;
④负值索引:倒数第一个元素的索引为-1,向前以此减1
⑤负值step:从后往前获取元素
2、多维ndarray中,每一维都叫一个轴axis。在ndarray中轴axis是非常重要的,有很多对于ndarray对象的运算都是基于axis进行,比如sum、mean等都会有一个axis参数(针对对这个轴axis进行某些运算操作):
对于多维数组,因为每一个轴都有一个索引,所以这些索引由逗号进行分割,例如:
>>> x = np.arange(0, 100, 5).reshape(4, 5)
>>> x
array([[ 0, 5, 10, 15, 20],
[25, 30, 35, 40, 45],
[50, 55, 60, 65, 70],
[75, 80, 85, 90, 95]])
>>> x[1,2] #第1行,第2列
35
>>> x[1:4, 3] #第1行到第3行中所有第3列的元素
array([40, 65, 90])
>>> x[:, 4] #所有行中的所有第4列的元素
array([20, 45, 70, 95])
>>> x[0:3, :] #第0行到第三行中所有列的元素
array([[ 0, 5, 10, 15, 20],
[25, 30, 35, 40, 45],
[50, 55, 60, 65, 70]])需要注意的是:
①当提供的索引比轴数少时,缺失的索引表示整个切片(只能缺失后边的轴)
②当提供的索引为:时,也表示整个切片
③可以使用...代替几个连续的:索引
另外,对于多为数组的迭代问题,可以使用ndarray的flat属性迭代数组中每一个元素:
>>> for item in x.flat:
... print item,
...
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95
四、⭐矩阵运算与线性代数:
这是文章的最大重点,运用numpy中带有的矩阵运算功能可以实现数值计算的所有基本操作,Python再这方面是十分强大而高效的!
部分函数功能是直接套在numpy里的,部分又是套在numpy.linalg里面的,所以下面进行一个简要的汇总:
包含在numpy里面的矩阵和向量计算常用基础功能:
dot |
两个数组的点积,即元素对应相乘。 |
vdot |
两个向量的点积 |
inner |
两个数组的内积 |
matmul |
两个数组的矩阵积 |
determinant |
数组的行列式 |
solve |
求解线性矩阵方程 |
inv |
计算矩阵的乘法逆矩阵 |
包含在numpy里面的矩阵和向量计算扩展功能:
| dot(a, b[, out]) | 两个数组的点积。 |
| linalg.multi_dot(arrays) | 在单个函数调用中计算两个或更多数组的点积,同时自动选择最快的求值顺序。 |
| vdot(a, b) | 返回两个向量的点积。 |
| inner(a, b) | 两个数组的内积。 |
| outer(a, b[, out]) | 计算两个向量的外积。 |
| matmul(x1, x2, /[, out, casting, order, …]) | 两个数组的矩阵乘积。 |
| tensordot(a, b[, axes]) | 沿指定轴计算张量点积。 |
| einsum(subscripts, *operands[, out, dtype, …]) | 计算操作数上的爱因斯坦求和约定。 |
| einsum_path(subscripts, *operands[, optimize]) | 通过考虑中间数组的创建,计算einsum表达式的最低成本压缩顺序。 |
| linalg.matrix_power(a, n) | 将方阵提升为(整数)n次方。 |
| kron(a, b) | 两个数组的Kronecker乘积。 |
包含在numpy.linalg里面的矩阵和向量分解功能:
| linalg.cholesky(a) | Cholesky分解 |
| linalg.qr(a[, mode]) | 计算矩阵的QR分解。 |
| linalg.svd(a[, full_matrices, compute_uv, …]) | 奇异值分解 |
包含在numpy.linalg里面的矩阵和向量特征值功能:
| linalg.eig(a) | 计算方阵的特征值和右特征向量。 |
| linalg.eigh(a[, UPLO]) | 返回复数Hermitian(共轭对称)或实对称矩阵的特征值和特征向量。 |
| linalg.eigvals(a) | 计算通用矩阵的特征值。 |
| linalg.eigvalsh(a[, UPLO]) | 计算复杂的Hermitian或实对称矩阵的特征值。 |
包含在numpy.linalg里面的矩阵和向量范数和其它数值功能:
| linalg.norm(x[, ord, axis, keepdims]) | 矩阵或向量范数。 |
| linalg.cond(x[, p]) | 计算矩阵的条件数。 |
| linalg.det(a) | 计算数组的行列式。 |
| linalg.matrix_rank(M[, tol, hermitian]) | 使用SVD方法返回数组的矩阵的rank |
| linalg.slogdet(a) | 计算数组行列式的符号和(自然)对数。 |
| trace(a[, offset, axis1, axis2, dtype, out]) | 返回数组对角线的和。 |
包含在numpy.linalg里面的矩阵和向量解矩阵和求逆功能:
| linalg.solve(a, b) | 求解线性矩阵方程或线性标量方程组。 |
| linalg.tensorsolve(a, b[, axes]) | 对x求解张量方程a x = b。 |
| linalg.lstsq(a, b[, rcond]) | 返回线性矩阵方程的最小二乘解。 |
| linalg.inv(a) | 计算矩阵的(乘法)逆。 |
| linalg.pinv(a[, rcond, hermitian]) | 计算矩阵的(Moore-Penrose)伪逆。 |
| linalg.tensorinv(a[, ind]) | 计算N维数组的“逆”。 |
包含在numpy.linalg里面的异常解决功能:
| linalg.LinAlgError | 泛型Python-linalg函数引发的异常派生对象。 |
上面列出的几个线性代数例程能够一次计算几个矩阵的结果,如果它们堆叠在同一数组中的话。
这在文档中通过输入参数规范(如 a : (..., M, M) array_like )表示。 这意味着,例如,如果给定输入数组 a.shape == (N, M, M) ,则将其解释为N个矩阵的“堆栈”, 每个矩阵的大小为M×M。类似的规范也适用于返回值, 例如行列式 det : (...) 。并且在这种情况下将返回形状 det(a).shape == (N,) 的数组。 这推广到对高维数组的线性代数操作:多维数组的最后1或2维被解释为向量或矩阵,视每个操作而定。
下面我们用几个具体一点的应用功能来描述:
1、范数计算:
numpy.linalg.norm(x, ord=None, axis=None, keepdims=False)
其中x代表要度量的向量。ord表示范数的种类,不填就是默认二范数,或者ord=2也是二范数,ord=1是一范数,ord=np.inf是无穷范数。axis是处理类型,axis=1表示按行向量处理求多个行向量的范数,axis=0表示按列向量处理求多个列向量的范数,axis=None表示矩阵的范数。keepdims参数表示是否保持矩阵的二维特性,True表示保持,False则相反。
2、求逆矩阵:
可以先使用mat方法创建一个矩阵,也即是:
data=numpy.array([a11,a12,a13], [a21,a22,a23], [a31,a32,a33])
然后调用inv求逆的函数对象进行计算:
reverse_data=numpy.linalg.inv(data)
注意!求解的矩阵必须是方阵而且可逆(非奇异矩阵才可逆),否则会抛出上述提到过的linalg.LinAlgError异常。
3、求方程组的精确解:
学过高等代数后,我们知道任何一个方程组都可以表示成AX=B的形式,其中A是系数矩阵,B是一个矩阵或者一个列向量,然后X是我们需要的解向量。
于是通过array方法创建A和B数组,也即是:
A=numpy.array([a11,a12], [a21,a22])
B=numpy.array([b1,b2])
然后调用解函数对象:
X=numpy.linalg.solve(A, B)
返回的X就是我们需要的解向量。
4、计算矩阵的行列式:
先用array方法创建一个矩阵数组,方法同上。
determinant=numpy.linalg.det(data)
直接调用data矩阵即可,这个很简单。
5、求矩阵的特征值与特征向量:
可以先使用mat方法创建一个矩阵,具体语法上面已经提到。
然后调用eigvals对象求矩阵的特征值:
characteristic_number=numpy.linalg.eigvals(data)
返回到特征值变量中会是一个包含了矩阵所有特征值的array数组。
或者也可以调用eig对象求方阵的特征值以及特征向量:
characteristic_number1,characteristic_number2, characteristic_number3=numpy.linalg.eig(data)
返回到特征值变量中会是一个包含了矩阵所有特征值的array数组和一个包含了所有特征向量的matrix矩阵。
6、奇异值分解:
SVD也就是奇异值分解,将一个矩阵分解成三个矩阵的乘积,data=U*Sigma*V,其中U和V都是正交矩阵,Sigma包含所有输入矩阵的奇异值。同样还是先用mat方法创建矩阵data。
然后调用奇异值分解函数功能:
U, Sigma, V=numpy.linalg.svd(data, full_matrices=False)
其中后一个参数是形状自定义。这个不需要深入了解,只需要赋值False基本上都能解决我们的需求。
7、QR分解:
将矩阵data分解成QR乘积,其中Q为正交矩阵R为上三角阵。
Q, R=numpy.linalg.qr(data, full_matrices=False)
同样地,后一个参数是形状自定义。这个不需要深入了解,只需要赋值False基本上都能解决我们的需求。
8、线性方程组的最小二乘解:
这是迭代方式解决线性方程组,与上面提到的精确解方式不同,这种方式比较适合极其复杂数据极其庞大的系数矩阵和解向量而求得近似解的过程。
y=mx+c二元一次回归函数,通过最小二乘方法求得参数m和c的值,再Numpy模块下有:
numpy.linalg.lstsq(array_A, array_B)[0]
其中,A是一个nX2的数组,B是一个1Xn的数组。A表示的是[x,1]的n个列表,1表示当前自变量对应点要考虑,x是所有点的横坐标。B表示[y]的一个列表,列表中包含依照顺序的n个因变量的值。这里A和B的结构比较难理解,需要动手实操熟悉熟悉。
五、SciPy科学计算库:
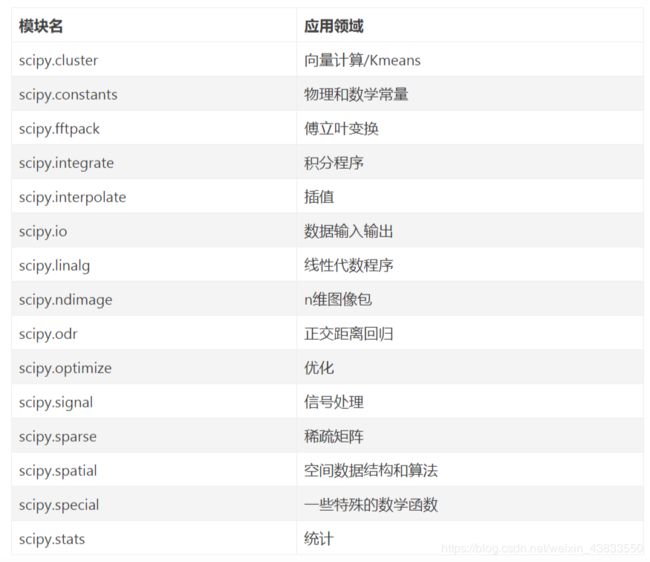
scipy包含致力于科学计算中常见问题的各个工具箱。它的不同子模块相应于不同的应用。像插值,积分,优化,图像处理,统计,特殊函数等等。
scipy可以与其它标准科学计算程序库进行比较,比如GSL(GNU C或C++科学计算库),或者Matlab工具箱。scipy是Python中科学计算程序的核心包; 它用于有效地计算numpy矩阵,来让numpy和scipy协同工作。
在实现一个程序之前,值得检查下所需的数据处理方式是否已经在scipy中存在了。作为非专业程序员,科学家总是喜欢重新发明造轮子,导致了充满漏洞的,未经优化的,很难分享和维护的代码。相反,Scipy程序经过优化和测试,因此应该尽可能使用。
1、认识SciPy的常用模块及功能:
2、从六个常用的SciPy功能块来详细分析其用途:
(1)积分运算:
scipy.integrate是SciPy功能包中提供的一个用于积分运算的模块,其中包含有多个不同的函数用于计算多种不同类型的积分式。这里我们首先强调:SciPy中的积分运算均是数值积分,也就是利用黎曼积分公式或者复合梯形公式通过无限分割的方式逼近与积分的真值。
最通用的积分程序是scipy.integrate.quad(func, a, b, args, full_output):
from scipy.integrate import quad
def integrand(x,a,b):
return a*x**2+b
a=2
b=1
I=quad(integrand, 0, 1, args=(a,b))
print(I)这里示例用的是ax^2+b这个二次函数。quad函数的四个参数分别是:自定义的积分函数表达式,积分下限,积分上限和积分函数中含有的参数具体值的元组args。计算的最终结果I是一个二元的元组,第一个数为积分的近似值,第二个数为积分的误差估计。
除此以外就是二重积分、三重积分和多变量积分的计算函数dblquad、tplquad和nquad:
二重积分的使用格式是:
scipy.integrate.dblquad(func, a, b,afunc, bfunc)
其中,func是一个函数名,a是外积分下限,b是外积分上限, afunc是内积分下限,bfunc是内积分上限。func函数的表达方式可以利用上面一重积分时候的自定义方式,但是如果随着维数增加,想要简化代码,也可以考虑lambda方法:
#普通方法定义函数func:
# 被积函数,y和x的排序必须是按照积分限制由外到内的顺序
def func(y, x)
return x*y
# 虽然下限是常数,但是还是写成函数形式
def afunc(x)
return 0
# 上限x
def bfunc(x)
return x
# 需要注意,func的参数顺序需要对应被积变量的顺序,比如本例就是先积分y,再积分x。
integrate(func, 1, 2, afunc, bfunc)
#lambda方法定义函数func:
integrate(lambda y, x : x*y, 1, 2, lambda x : 0, lambda, x : x)
三重积分的使用格式:
scipy.integrate.tplquad(func, a, b,afunc, bfunc, gfun, hfun)
相当于再在二重积分上增加了第三层积分表达式的上下限,函数定义仍然遵从上述要求。
多变量积分的使用格式:
scipy.integrate.nquad(func, ranges)
ranges是按照由外到内每一层积分下限、上限构成的表。其它的功用实际上就是二、三重积分的扩展,与上述类似。
(2)矩阵行列式:
仍然是利用linalg.det,只不过是scipy.linalg.det(data),和上述Numpy中的det对象效果完全一样,用法也完全一样,data同上也是利用array建立的矩阵数组,打印返回值即可看到行列式的计算结果。这里scipy中行列式计算函数det用的是行列式展开计算的方法。
(3)逆矩阵:
scipy.linalg.inv(data)用法与上面总结的也是完全相同的,这里会运用矩阵求逆运算的准确计算方式完成。当然如果以numpy.float64来存储数据,会有四舍五入,但精确值仍然是极高的。
(4)求解方程组:
scipy.linalg.solve()解线性方程组是很简单的。此方法需要输入系数矩阵和等号右侧的列向量,然后计算解向量,与之前提到的方式也基本相同。求解的原理就是AX=B,键入了A矩阵和B向量后,利用X=A^(-1)*B来计算解向量。这也就意味着如果A是一个奇异矩阵,此方法不是很好用。
(5)最小二乘法拟合:
如果f是一个线性函数f(x)=kx+b,那么参数k和b就是去需要计算确定的值,如果将这些参数用p来表示,那么就要找到一组p的值,使得如下公式中的S函数值最小:
这种算法就是最小二乘拟合,以及scipy中最小二乘拟合功能的实现原理。这里scipy.optimize是用来实现拟合的功能模块。
首先我们需要定义数据拟合所需的函数:
import numpy as np
from scipy import linalg
def fun(x,p):
A,k,theta=p
return A*np.sin(2*np.pi*k*x+theta)然后定义我们的拟合误差函数,实验数据x,y和拟合函数的差需要通过这个误差估计函数来算,参数p为拟合需要找到的系数,同时添加噪声。
def residuals(p,y,x):
return y-func(x,p)
x=np.linspace(0,-2*np.pi,100)
A,k,theta=10,0.34,np.pi/6
y0=func(x,[A,k,theta])
y1=y0+2*np.random.randn(len(x))
p0=[7,0.2,0]其中后面四行代码分别是:真实数据的函数参数定义,真实数据的导入y0,加如噪声后的实验数据导入y1,第一次猜测的函数拟合参数,相当于迭代初始值存入p0。
然后我们调用scipy.linalg中的leastsq函数进行拟合:
plsq=leastsq(residuals,p0,args=(y1,x))
print("真实参数:",[A,k,theta])
print("拟合参数:",plsq[0])
其中第一个参数为误差估计函数residuals,第二个参数是迭代起点p0,args代表需要拟合的函数中的参数列表。先然,这样的代码运行之后便能很快得到我们需要的误差范围内的拟合值,效果是很好的。
通过matplotlib模块,还能够进行数据可视化工作,也就是把拟合的曲线和原始的数据进行图像对比。具体的plot的那些函数功能会在后续的文章中进行介绍,此略。
(6)SciPy图像处理基础:
scipy中致力于图像处理的子模块是scipy,ndimage。
from scipy import ndimage图像处理程序可以根据它们执行的操作类别来分类。
①图像的几何变换:
图像的几何变换包括改变方向,分辨率等:
from scipy import misc
lena = misc.lena()
shifted_lena = ndimage.shift(lena, (50, 50))
shifted_lena2 = ndimage.shift(lena, (50, 50), mode='nearest')
rotated_lena = ndimage.rotate(lena, 30)
cropped_lena = lena[50:-50, 50:-50]
zoomed_lena = ndimage.zoom(lena, 2)
zoomed_lena.shape(1024, 1024)
pl.subplot(321)
pl.imshow(lena, cmap=cm.gray)
pl.subplot(322)
#等 ②图像的滤镜:
图像的滤镜功能包括图像加噪声、高斯滤波、中值滤波和维纳滤波等等:
from scipy import misc
lena = misc.lena()
import numpy as np
noisy_lena = np.copy(lena).astype(np.float)
noisy_lena += lena.std()*0.5*np.random.standard_normal(lena.shape)
blurred_lena = ndimage.gaussian_filter(noisy_lena, sigma=3)
median_lena = ndimage.median_filter(blurred_lena, size=5)
from scipy import signal
wiener_lena = signal.wiener(blurred_lena, (5,5))
文章篇幅有限,能够介绍的只是一些常用的十分基础的功能,实际上Numpy和SciPy是Python十分强大的科学库功能,可以实现我们日常工程计算中几乎所有的功能,甚至还能协同导入Matlab的文件进行二次处理。运用好了这些个函数可以让我们的计算工作变得如鱼得水。以后也不必辛辛苦苦手算、按计算器或者上百度查在线矩阵计算网站了。
![S(p)=\sum_{i=1}^{m}[y_{i}-f(x_{i},p)]^2](http://img.e-com-net.com/image/info8/167580d19c3c485eae4bd9d247b94c4c.gif)