基本的算法设计技术——贪心法

1.一个简单的例子——埃及分数
完整代码：

#include<iostream>
using namespace std;

int CommFactor(int m,int n)
{
    int r=m%n;
    while(r!=0) 
    {
    	m=n;
    	n=r;
    	r=m%n;
    }
    return n;
}

void EgyptFraction(int A,int B)
{
	int E,R;
	cout<<A<<"/"<<B<<"=";
	do
	{
		E=B/A+1;
		cout<<"1/"<<E<<"+";
		A=A*E-B;
		B=B*E;
		R=CommFactor(B,A);
		if(R>1)
		{
			A=A/R;
			B=B/R;	
		}	
	}while(A>1);
	cout<<"1/"<<B;
} 
int main( )
{
	int A, B;
	cout<<"请输入真分数的分子：";
	cin>>A;
	cout<<"请输入真分数的分母：";
	cin>>B;
    EgyptFraction(A, B);
	return 0;
}

运行结果：

2.图问题中的贪心法
1>TSP问题
完整代码：

#include<iostream>
#define max 100
using namespace std;
const int n = 5;
int TSP1(int arc[n][n],int w)
{
	int edgeCount=0,TSPLength=0;
	int min,u,v;
	int flag[n]={0};
	u=w; flag[w]=1;
	while(edgeCount<n-1)
	{
		min=1000;
		for(int j=0;j<n;j++)
		{
			if((flag[j]==0)&&(arc[u][j]!=0)&&(arc[u][j]<min))
			{
				v=j;
				min=arc[u][j];
			}
		}
		TSPLength+=arc[u][v];
		flag[v]=1;
		edgeCount++;
		cout<<u<<"-->"<<v<<endl;
		u=v;
	}
	cout<<v<<"->"<<w<<endl;
	return (TSPLength+arc[u][w]);
}
int main( )
{
	int arc[n][n] = {{max,3,3,2,6},{3,max,7,3,2},{3,7,max,2,5},{2,3,2,max,3},{6,2,5,3,max}};
	int minDist = TSP1(arc, 0);
	cout<<"最短哈密顿回路的长度是："<<minDist<<endl;
	return 0;
}

运行结果：

2>图着色问题
完整代码：

#include<iostream>
using namespace std; 
const int N = 5;
int arc[N][N]={{0,1,0,0,0},{1,0,1,1,0},{0,1,0,0,1},{0,1,0,0,1},{0,0,1,1,0}};
int color[N] = {0};
//函数Ok判断顶点i的着色与其他顶点的着色是否发生冲突 
int Ok(int i)
{
	for(int j=0;j<N;j++)
	{
		if(arc[i][j]==1&&color[i]==color[j])
			return 0;
	}	
	return 1;
} 

void ColorGraph()
{
	int k=0;
	int flag=1;//flag=1表示图中还有尚未涂色的顶点 
	while(flag==1)
	{
		k++; flag=0;  
		for(int i=0;i<N;i++)
		{
			if(color[i]==0)
			{
				color[i]=k; //顶点i涂颜色k 
				if(!Ok(i))  //发生冲突，取消涂色 
				{
					color[i]=0;
					flag=1;
				}
			}
		}
	}	
} 

int main( )
{
	ColorGraph();
	for(int i=0;i<N;i++)
		cout<<color[i]<<" ";
	return 0;
}

运行结果：

3>最小生成树问题
完整代码：

#include<iostream>
using namespace std;
const int n = 6;
const int max1 = 100;

typedef struct
{
	int lowcost;//候选最短边的权值 
	int adjvex;//候选最短边的邻接点 
}Element;

void Prim(int arc[n][n], int w)//从顶点w开始构造最小生成树 
{
	int i, j, k;
	int min;
	Element shortEdge[10];//候选最短边集 
	for(i=0;i<n;i++)//初始化辅助数组shortEdge
	{
		shortEdge[i].lowcost=arc[w][i];//将各点候选最短边的权值初始化为各点和顶点w连线的距离（无连线的初始化为max） 
		shortEdge[i].adjvex=w;//上一步将各点候选最短边的权值初始化为各点和顶点w连线的距离（无连线的初始化为max）,因此各点初始邻接点都是w 
	}
	shortEdge[w].lowcost = 0;//将顶点w加入集合U，不作为候选点了，因此候选最短边的权值(候选点到集合U中的点的连线的最短距离)为0 
	for(i=0;i<n-1;i++) 
	{
		min=100;
		for(j=0;j<n;j++)//寻找最短边的邻接点k
		{
			if((shortEdge[j].lowcost!=0)&&(shortEdge[j].lowcost<min))//等于0的已经加入集合U中，找出到集合U中的点连线最小的候选点 
			{
				min=shortEdge[j].lowcost;
				k=j;//将找出的到集合U中的点连线最小的候选点赋值给k，以便于作为下一个放入集合U中的点 
			}
		}
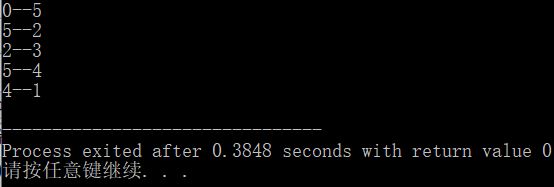
        cout<<shortEdge[k].adjvex<<"--"<<k<<endl;//将k放入集合U之前先输出k的邻接点和k 
		shortEdge[k].lowcost=0;//将顶点k加入集合U中
		for(j=0;j<n;j++)//调整数组shortEdge[n]，因集合U中的元素增加了，因此数组shortEdge[n]中的候选点到集合U中的点的连线的最短距离和候选最短边的邻接点变化了 
		{
			if(arc[k][j]<shortEdge[j].lowcost)//新加入集合U的点与各点连线的距离若小于数组shortEdge[n]中候选最短边的权值，则更新数组shortEdge[n]
			{
				shortEdge[j].lowcost = arc[k][j];
				shortEdge[j].adjvex = k;
            }
		}
    }
}

int main( )
{
	int arc[n][n] = {
		{max1, 34, 46, max1,max1,19},
		{34, max1, max1,max1,12, max1},
		{46, max1, max1, 17, max1, 25},
		{max1, max1, 17, max1, 38, 25},
		{max1, 12, 38, max1, 26},
		{19, max1, 25, 25, 26, max1}
	};
	Prim(arc, 0);
	return 0;
}

运行结果：

3.组合问题中的贪心法
1>背包问题
背包问题与0/1背包问题类似，所不同的是在选择物品i装入背包时，可以选择一部分，而不一定要全部装入背包。背包问题可以用贪心法求解，而0/1背包问题却不能用贪心法求解，0/1背包问题适合用动态规划法求解。
完整代码：

#include<iostream>
using namespace std;
const int n = 3;

int KnapSack(int w[ ], int v[ ], int n, int C)
{
	double x[10]={0};//物品可部分装入
	int maxValue=0;
	int i;
	for(i=0;w[i]<C;i++)
	{	
		x[i]=1;
		maxValue+=v[i];
		C=C-w[i];
	}	
	x[i]=(double)C/w[i];
	maxValue+=x[i]*v[i];
	return maxValue;
} 

int main()
{
	int w[n] = {10, 30, 20}, v[n] = {50, 120, 60};
	int C = 50;
	int value = KnapSack(w, v, 3, C);
	cout<<"背包获得的最大价值是："<<value<<endl;
	return 0;
}

运行结果：

2>活动安排问题

#include<iostream>
using namespace std;
const int n = 11;

int ActiveManage(int s[ ], int f[ ], int B[ ], int n)
{  
   int i,j,count;
   B[0]=1;
   j=0;
   count=1;
   for(i=1;i<n;i++)
   {
   	if(s[i]>=f[j])
   	{
   		B[i]=1;
   		j=i;
   		count++;
   	}
   	else
   		B[i]=0;
   }
   return count;
}

int main( )
{
   int s[n] = {1,3,0,5,3,5,6,8,8,2,12};
   int f[n] = {4,5,6,7,8,9,10,11,12,13,14};
   int B[n] = {0};
   int k = ActiveManage(s, f, B, n);
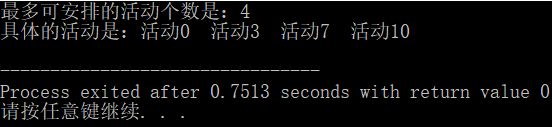
   cout<<"最多可安排的活动个数是："<<k<<endl;
   cout<<"具体的活动是：";
   for (int i = 0; i < n; i++)
   	if (B[i] == 1)
   		cout<<"活动"<<i<<"  ";
   cout<<endl;
   return 0;
}

运行结果：

3>多机调度问题
1）教材上（按时间从大到小排好序）：
完整代码：

#include<iostream>
#include<string.h>
using namespace std;
const int n = 7;
const int m = 3;

void MultiMachine(int t[ ], int n, int d[ ], int m)
{
	int S[m][n]={{-1,-1,-1,-1,-1,-1,-1},{-1,-1,-1,-1,-1,-1,-1},{-1,-1,-1,-1,-1,-1,-1}};
	int rear[m];     //S[i]为存储机器i处理作业的队列，rear[i]为队尾下标
	int i, j, k;
	for(i=0;i<m;i++)
	{
		S[i][0]=i;
		rear[i]=0;
		d[i]=t[i];
	}
	for(i=m;i<n;i++)
	{
		for(j=0,k=1;k<m;k++)
		{
			if(d[k]<d[j])
				j=k;
		}	
		rear[j]++;
		S[j][rear[j]]=i;
		d[j]+=t[i]; 
	} 
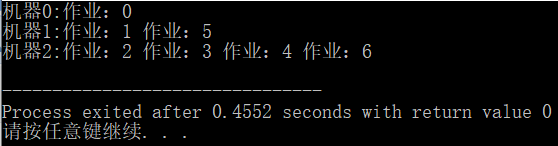
	for(i=0;i<m;i++)
	{
		cout<<"机器"<<i<<":";
		for(j=0;S[i][j]>=0;j++)
			cout<<"作业："<<S[i][j]<<" "; 
		cout<<endl;
	}
}

int main( )
{
	int t[n] = {16, 14, 6, 5, 4, 3, 2};
	int d[m] = {0};
    MultiMachine(t, n, d, m);
	return 0;
}

运行结果：

2）未按时间从大到小排序：
完整代码：

#include<iostream>
//定义最大作业数量
#define MAXLENGTH 10
//定义机器的空闲时间
using namespace std;
int d[MAXLENGTH];
//定义每台机器的处理时间
int S[MAXLENGTH][MAXLENGTH];
//定义一个结构体，记录作业处理时间
struct work{
	//作业时间
	int hour;
	//原顺序
	int number;
};
work t[MAXLENGTH];
//数组的排序算法
void bubble_sort(work a[], int n){
	int i, j;
	work temp;
	for(j=0;j<n-1;j++){
		for (i=0;i<n-1-j;i++)
		{
			if(a[i].hour<a[i+1].hour)
			{
				temp=a[i];
				a[i]=a[i + 1];
				a[i+1]=temp;
			}
		}
	}
}
//多机调度算法声明
void MultiMachine(work t[], int n, int d[], int m);
int main(){
	//作业个数
	int n;
	//机器个数
	int m;
	//用于计数
	int i;
	cout<<"请输入待处理的作业个数:";
	cin>>n;
	cout<<"请输入作业需要处理的时间:";
	for(i=0;i<n;i++)
	{
		cin>>t[i].hour;
		t[i].number=i+1;
	}
	//将结构体数组进行从大到小的排序，序号存在number中
	bubble_sort(t, n);
	cout<<"请输入机器的个数:";
	cin>>m;
	//将数组d初始化为0
	for(i=0;i<m;i++)
	{
		d[i]=0;
	}
	MultiMachine(t, n, d, m);
}

void MultiMachine(work t[],int n,int d[],int m){
	//队尾下标
	int rear[MAXLENGTH];
	int i,j,k;
	//安排前m个作业
	for(i=0;i<m;i++)
	{
		S[i][0]=t[i].number;
		rear[i]=0;
		d[i]=t[i].hour;
	}
	//一次安排余下几个作业
	for(i=m;i<n;i++)
	{
		//查找最先空闲的机器
		for(j=0,k=1;k<m;k++)
		{
			if(d[k]<d[j])
			{
				j=k;
			}
		}
		rear[j]++;
		S[j][rear[j]] = t[i].number;
		d[j]+=t[i].hour;
	}
	//输出结果
	for(i=0;i<m;i++)
	{
		cout<<"机器"<<i+1<<"处理:";
		for(j=0;S[i][j]>0;j++)
		{
			cout<<"作业"<<S[i][j]<<" ";
		}
		cout<<"处理时间:"<<d[i]<<endl;
	}
}

运行结果：