ALS算法--交替最小二乘算法

算法概述：

 

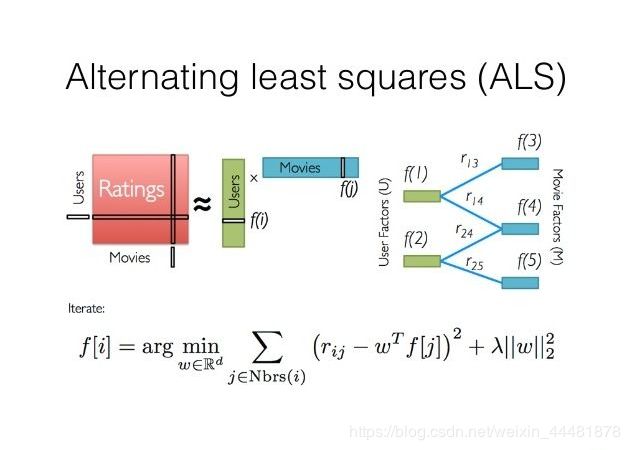
ALS是交替最小二乘（alternating least squares）的简称。在机器学习中，ALS特指使用交替最小二乘求解的一个协同推荐算法。它通过观察到的所有用户给商品的打分，来推断每个用户的喜好并向用户推荐适合的商品。比如下图：

这个矩阵的每一行代表一个用户（u1,u2,u3）、每一列代表一个商品（v1,v2,v3）、用户的打分为1-5分。这个矩阵只显示了观察到的打分，我们需要推测没有观察到的打分。比如（u1，v3）打分多少？如果以数独的方式来解决这个问题，可以得到唯一的结果。 因为数独的规则很强，每添加一条规则，就让整个系统的自由度下降一个量级。当我们满足所有的规则时，整个系统的自由度就降为1了，也就得出了唯一的结果。对于上面的打分矩阵，如果我们不添加任何条件的话，也即打分之间是相互独立的，我们就没法得到（u1，v3）的打分。 所以在这个用户打分矩阵的基础上，我们需要提出一个限制其自由度的合理假设，使得我们可以通过观察已有打分来猜测未知打分。

ALS的核心就是这样一个假设：打分矩阵是近似低秩的。换句话说，就是一个U*I的打分矩阵可以由分解的两个小矩阵U（U*k）和I（k*I）的乘积来近似。这就是ALS的矩阵分解方法。

ALS算法原理

如何算得因子矩阵里的因子数值是ALS算法要解决的问题，这需要一个明确的可量化目标，ALS用每个元素重构误差的平方和来进行量化。

因为在原评级矩阵中，大量未知元是我们想推断的，所以这个重构误差是包含未知数的。 而ALS算法的解决方案很简单：只计算已知打分的重构误差。

ALS的实现原理是迭代式求解一系列最小二乘回归问题。在每一次迭代时，固定用户因子矩阵或是物品因子矩阵中的一个，然后用固定的这个矩阵以及评级数据来更新另一个矩阵。之后，被更新的矩阵被固定住，再更新另外一个矩阵。如此迭代，直到模型收敛（或是迭代了预设好的次数）。

所以在MLlib的ALS算法中，首先对U或者I矩阵随机化生成，在每一次迭代时，固定用户因子矩阵或是物品因子矩阵中的一个，然后用固定的这个矩阵以及评级数据来更新另一个矩阵，然后利用被求取的矩阵对象去求随机化矩阵。最后两个对象相互迭代计算，直到模型收敛。

ASL算法推导

ASL对于显式矩阵分解的损失函数：

其中，r是打分（原始）矩阵，r(i，j）表示用户i对物品j的实际打分。

UiIj是根据用户和商品的隐藏因子矩阵算得的值，

所以：某一个物品评分的误差=（实际打分-计算值）^2

λ是正则化的参数。正规化是为了防止过拟合的情况发生。

在算法执行中，比如先随机化I(物品隐藏因子矩阵），并固定之，然后对U（用户隐藏因子矩阵）在损失函数L（U,I）上求偏导，因为ALS算法本质是最小二乘法，所以令其导数=0

举个简单的例子，假设我们有如下用户对电影的评级数据：

Tom, Star Wars, 5

Jane, Titanic,  4

Bill, Batman,  3

Jane, Star Wars, 2

Bill, Titanic, 3

它们可转为如下评级矩阵：

为了更好的实现推荐系统，我们需要对这个稀疏的矩阵建模。一般可以采用矩阵分解（或矩阵补全）的方式。

具体就是找出两个低维度的矩阵，使得它们的乘积是原始的矩阵。因此这也是一种降维技术。假设我们的用户和物品数目分别是U和I，那对应的“用户-物品”矩阵的维度为U×I，如下图所示：

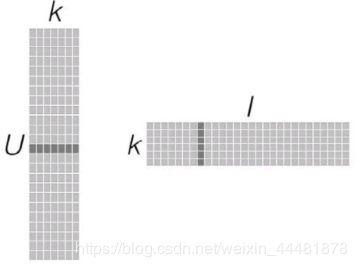
要找到和“用户-物品”矩阵近似的k维（低阶）矩阵，最终要求出如下两个矩阵：一个用于表示用户的U×k维矩阵，以及一个表征物品的k×I维矩阵。这两个矩阵也称作因子矩阵。它们的乘积便是原始评级矩阵的一个近似。值得注意的是，原始评级矩阵通常很稀疏，但因子矩阵却是稠密的（满秩的），如下图所示：

这类模型试图发现对应“用户-物品”矩阵内在行为结构的隐含特征（这里表示为因子矩阵），所以也把它们称为隐特征模型。隐含特征或因子不能直接解释，但它可能表示了某些含义，比如对电影的某个导演、种类、风格或某些演员的偏好。

k隐藏因子的取值有一定的约束：

1.k一般是低阶，小于u和I

2.生产环境中，k的取值范围一般是10~50,不宜过小或是过大，如果k过大，会导致计算代价增大

由于是对“用户-物品”矩阵直接建模，用这些模型进行预测也相对直接：要计算给定用户对某个物品的预计评级，就从用户因子矩阵和物品因子矩阵分别选取相应的行（用户因子向量）与列（物品因子向量），然后计算两者的点积即可。如下图所示：

而对于物品之间相似度的计算，可以用最近邻模型中用到的相似度衡量方法。不同的是，这里可以直接利用物品因子向量，将相似度计算转换为对两物品因子向量之间相似度的计算，如下图所示：

因子分解类模型的好处在于，一旦建立了模型，对推荐的求解便相对容易。所以这类模型的表现通常都很出色。但弊端可能在于因子数量的选择有一定困难，往往要结合具体业务和数据量来决定。一般来说，因子的取值范围在10~200之间。注意：k越大，其计算复杂度越高