【你也能看得懂的电磁场与电磁波系列连载 16】

在上一个连载里面，我们成功推导出了 $Maxwell$ 方程的积分形式，一共有四个方程，分别描述电生磁、磁生电、磁场和电场，我们再来回顾一下：

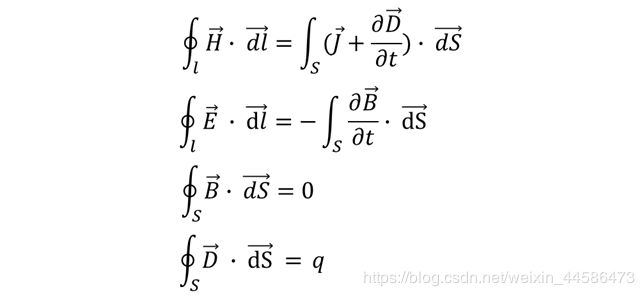
那么，在后续的几个连载里面，我们将会看看 $Maxwell$ 方程组的微分形式，到时候我们将会感叹科学家们伟大的创造力！首先，我们需要引入微分形式里面的重要人物——矢量微分算子。在此之前，我们先来看看什么是方向导数和梯度 ：

---

在一元函数里面，我们知道可以用导数反应函数的变化率：

所谓导数，定义就是：

我们看第一张图：$dx=△x$这个没问题，但是我们发现，其实$dy$ 并不等于$△y$ 。但是他们俩很接近。在一元函数里面，我们可以这样表示 $△y$：$$△y=y^{\prime }(M)△x+o(△x)$$
其中，$y^{\prime }(M)=\frac{dy}{dx}$，那很显然，$y^{\prime }(M)△x$ 就等于 $dy$，而我们刚刚不是说其实$dy$ 并不等于$△y$嘛，他们之间还差了那么一小段长度，这个很小的长度我们用 $o(△x)$ 表示 。如果这个高阶无穷小量 $o(△x)$ 咱们可以忽略不计，那么函数在 $△x$ 上的值的变化 $△y$ 我们就可以近似地写成：$$△y\approx y^{\prime }(M)△x\text{\hspace{1em}(1)}$$

---

那么，现在我们推广到二元函数，即型如：$f(x,y)$。

在刚刚的讨论里面我们知道，对于一元函数，因为他只有 $x$ 这一个自变量，所以我们很自然可以用：$\frac{dy}{dx}$来表示函数 $y(x)$ 沿着x轴方向变化的快慢。

但是对于二元函数呢，直接用 $\frac{df}{dx}$ 么？好像不太对，因为我们 $f(x,y)$ 是一个关于x和y的二元函数，它的变量有两个，你这样直接 $\frac{df}{dx}$ 合适么？

但是，如果我在考虑x轴方向的时候，把y看作一个常数，也就是把y轴固定住，这样函数 $f(x,y)$ 就只跟x相关了，于是我们就把一个二元函数（曲面）变成了一个一元函数（曲线）那么此时 $f(x,y)$ 对x的求导就可以反应在 x 方向的变化率。同理，在考虑 $y$ 方向时，把 x 固定住，这样函数就只跟 y 相关了，那么此时 $f(x,y)$ 对y的求导就可以反应在 y 方向的变化率

这就是偏导数的由来。

---

下面，我们以一个二元函数为例，在二元函数上找一点 A ，过A 点分别平行于 $xoz$ 和 $yoz$ 的平面（即分别把 $y$ 和 $x$ 固定）那么这两个平面截得的 $f(x,y)$ 的图像就是两根曲线了：

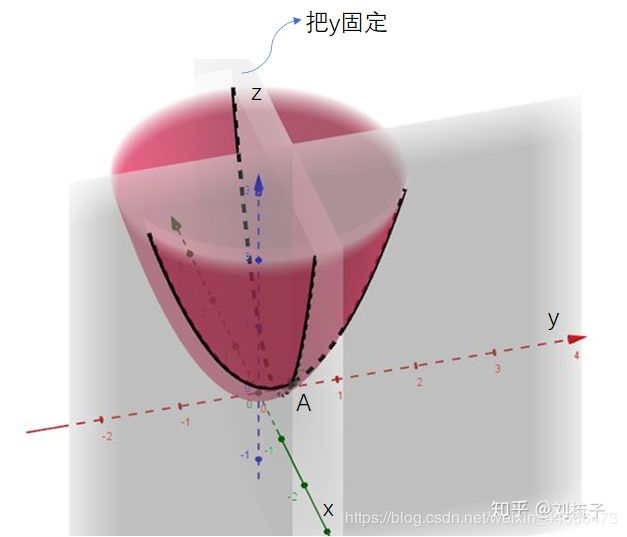
那么，偏导数就是两根曲线在 A 点处的切线，我们把他画出来：

这两根切线是共面的（事实上我们发现在 A 点是不是可以做无数条曲线，而这无数条曲线，每一条都会有自己的切线，巧合的是这所有的切线都是共面的！！）那么，我们先把上面这两条切线 $u,v$ 所在的平面画出来（这个平面也是所有经过A 点曲线的切线所在的平面）

那么有趣的事情就来了：在一元函数里面，我们不是可以用一点附近的切线代替 A 点附近的曲线嘛，那么在二元函数里面，我们就可以用 一点附近的切平面来代替一点来代替一点附近的曲面了

那么回顾我们在一元函数里面的表达：$$△y\approx \frac{dy}{dx}△x\text{\hspace{1em}(1)}$$

那么在二元函数里面，我们就可以写成：

这就是二元函数的全微分公式，那么继续推广到更高维也是类似的表达式。

---

说了半天为啥要讲全微分呢，这是为了引入方向导数和梯度的概念。大家记得我们最后推出来的这个式子，我们在下一个连载里面将会学习方向导数和梯度，并且引入矢量微分算子